Прямые уровня и проецирующие прямые – это важное понятие в геометрии, которое играет важную роль в изучении пространственных отношений и венчевания. Эти два термина связаны с методами определения и визуализации прямых линий в трехмерном пространстве.
Прямые уровня – это прямые, которые параллельны плоскости наблюдения. Они получаются при проецировании прямых линий на эту плоскость. Прямые уровня имеют замечательное свойство – они постоянно расстояние от плоскости наблюдения. Именно это свойство дает им такое название – прямые уровня.
Проекционные прямые – это прямые, которые отображаются в конечную точку на плоскости наблюдения. Они также получаются при проецировании прямых линий на эту плоскость, но в отличие от прямых уровня они не являются параллельными. Вместо этого они пересекают плоскость наблюдения и образуют отдельные точки.
Прямые уровня и проецирующие прямые – это ключевые понятия геометрии, которые позволяют анализировать и описывать пространственные объекты. Понимание этих понятий и их свойств помогает в решении многих геометрических задач и находит применение в различных областях науки и техники.
Определение прямых уровня и проецирующих прямых
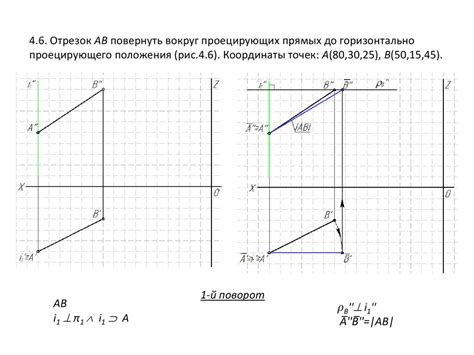
Прямые уровня – это линии, которые используются для измерения относительных высот местности. Они строятся в плане и суть совокупность точек, находящихся на одной высоте относительно опорной поверхности.
Проецирующие прямые представляют собой линии, которые соблюдают определенные условия проекционной геометрии. Они призваны упрощать построение различных фигур и объектов на плоскости. Проецирующие прямые также важны при создании картографических проекций и геодезических сетей.
| Прямые уровня | Проецирующие прямые |
|---|---|
| Служат для измерения относительных высот | Облегчают построение фигур на плоскости |
| Строятся в плане | Применяются в проекционной геометрии |
| Находятся на одной высоте относительно опорной поверхности | Используются в картографии и геодезии |
Прямые уровня и их особенности
Основной характеристикой прямых уровня является то, что они не содержат точек с обоими параллельными осями. Другими словами, прохождение прямой через начало координат делает ее не-прямой уровней, так как начало координат имеет значения (0, 0, 0).
Прямые уровня также отличаются от проецирующих прямых тем, что они не параллельны никакой из осями координатов. Прямая уровня может иметь направление, которое задается своими точками ориентации, но она не будет параллельна ни одной из осей.
Кроме того, прямые уровня обеспечиваются симметрической группой, называемой группой движений. Это означает, что любое движение, сохраняющее расстояние между точками, также сохраняет их положение на прямой уровня. Это свойство делает прямые уровня полезными в геометрических преобразованиях и алгоритмах.
Итак, прямые уровня являются особыми прямыми, которые не проходят через начало координат и не параллельны ни одной из осей координат. Они обладают особенностями, которые делают их полезными в решении задач геометрии и линейной алгебры.
Проектирующие прямые и их характеристики
Проектирующие прямые имеют несколько основных характеристик:
1. Направление:
Каждая проектирующая прямая имеет определенное направление. Оно может быть вертикальным, горизонтальным или наклонным. Направление прямой определяется ее углом наклона к основной плоскости или линии.
2. Длина:
Длина проектирующей прямой зависит от требований конкретного построения или задачи. Она может быть произвольной, но соответствующей установленным условиям.
3. Положение:
Положение проектирующей прямой определяется ее начальной точкой отсчета и ориентацией в пространстве. Оно может быть абсолютным или относительным, что зависит от системы координат или других факторов конкретной задачи.
Использование проектирующих прямых позволяет строить и анализировать геометрические фигуры, определять их характеристики, находить точки пересечения и многое другое. Они широко применяются в различных областях, таких как архитектура, инженерия и дизайн.
Учение о проектирующих прямых и их характеристиках является важной составляющей математического образования и позволяет развивать навыки пространственного мышления и аналитического мышления у студентов и учащихся.
Различие между прямыми уровня и проецирующими прямыми
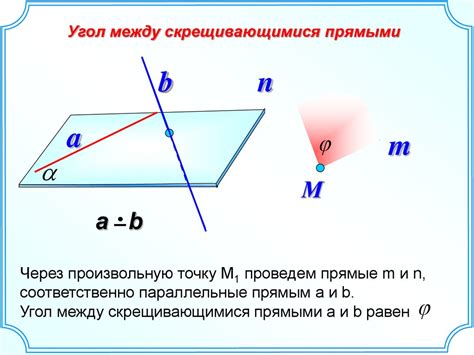
Прямые уровня - это прямые, которые находятся внутри плоскости и пересекают ее параллельно. Они сохраняют свое положение и направление в пространстве, не меняясь при переносе или повороте плоскости. Прямые уровня можно представить как нити, которые протянуты через плоскость и параллельны друг другу.
Проецирующие прямые, с другой стороны, пересекают плоскость не параллельно, а под углом. Они имеют склонность менять свое положение и направление при изменениях положения или ориентации плоскости. Проецирующие прямые используются в проекционных системах, где они помогают создавать трехмерное изображение на двухмерной плоскости.
Таким образом, основное различие между прямыми уровня и проецирующими прямыми заключается в их отношении к плоскости. Прямые уровня параллельны плоскости и не меняют свое положение, в то время как проецирующие прямые пересекают плоскость под углом, изменяясь при изменении положения плоскости.
Геометрические отличия между прямыми уровня и проецирующими прямыми

Прямые уровня представляют собой прямые линии, которые расположены на плоскости и имеют постоянную высоту относительно опорной поверхности. Они обычно используются в геодезии и картографии для обозначения местности, такую как рельеф и контуры. Прямые уровня помогают определить разницу высот между разными точками на земной поверхности и создают трехмерную модель местности.
Проецирующие прямые, с другой стороны, используются в проективной геометрии и имеют немного отличающуюся геометрию. Они являются прямыми линиями, которые пересекаются в плоскости бесконечности и создают прямую на данной плоскости. Проецирующие прямые широко применяются в изображении, графике и архитектуре для создания перспективного эффекта и глубины визуализации.
Таким образом, основная разница между прямыми уровня и проецирующими прямыми заключается в их функциях и целях использования. Прямые уровня используются для определения разницы высот на поверхности земли, тогда как проецирующие прямые используются для создания перспективных эффектов и глубины визуализации.
| Прямые уровня | Проецирующие прямые |
|---|---|
| Используются в геодезии и картографии | Используются в изображении и архитектуре |
| Определяют разницу высот на поверхности земли | Создают перспективный эффект и глубину визуализации |
| Лежат на плоскости и имеют постоянную высоту | Пересекаются в плоскости бесконечности |
Аналитическое сравнение прямых уровня и проецирующих прямых
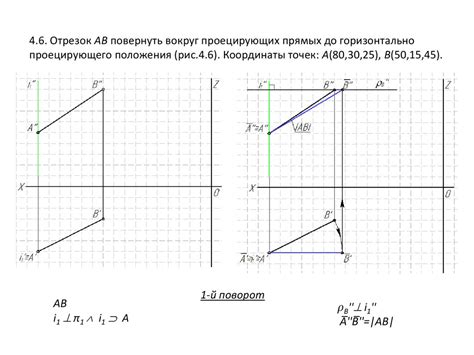
Прямая уровня – это прямая, которая пересекает все плоскости через одну точку и параллельна всем прямым, принадлежащим плоскости.
Проецирующая прямая – это прямая, проходящая через точку проекции и пересекающая плоскость проекции.
Одним из ключевых отличий между прямой уровня и проецирующей прямой является их расположение относительно объектов и плоскостей:
1. Прямая уровня находится вне плоскости, что позволяет ей пересечь все плоскости через одну точку.
2. Проецирующая прямая, напротив, пересекает плоскость проекции и позволяет создавать проекции объектов на эту плоскость.
Кроме того, прямая уровня и проецирующая прямая имеют различное влияние на процесс построения геометрических фигур:
1. Прямая уровня используется в построении плоских фигур и позволяет определить их геометрические параметры.
2. Проецирующая прямая, в свою очередь, играет важную роль при построении пространственных фигур и определении их размеров и формы.
Таким образом, прямая уровня и проецирующая прямая представляют собой два основных инструмента геометрии, которые используются для анализа и конструирования пространственных объектов, плоских фигур и их свойств.
Применение прямых уровня и проецирующих прямых в практике

Прямые уровня используются в архитектуре и строительстве. Они помогают определить горизонтальные линии и обеспечивают правильное расположение элементов конструкции. Например, при строительстве стен или пола, использование прямых уровня гарантирует, что поверхность будет ровной и горизонтальной.
Проецирующие прямые также находят применение в архитектуре и строительстве. Они используются для создания перспективных планов и сечений зданий. Проецирующие прямые позволяют представить объект в виде проекций на плоскость, что упрощает его исследование и анализ.
В инженерии и машиностроении прямые уровня и проецирующие прямые применяются для разработки и изготовления деталей и механизмов. Они помогают определить правильные размеры и формы деталей, а также обеспечивают их точное расположение в пространстве. Благодаря использованию этих прямых, инженеры и машинисты могут создавать сложные системы и конструкции, соответствующие требованиям проекта.
Прямые уровня и проецирующие прямые также находят применение в графике и дизайне. Они используются для создания правильных перспективных рисунков и изображений. Благодаря умению работать с этими прямыми, художники и дизайнеры могут создавать реалистичные и пропорциональные композиции.
Кроме того, прямые уровня и проецирующие прямые встречаются в области оптики. Они используются для расчета линейных размеров и глубины объективов, а также для определения путей преломления света. Профессионалы в области оптики используют эти прямые для создания и настройки оптических систем, таких как линзы и приборы.
Роли прямых уровня и проецирующих прямых в строительстве
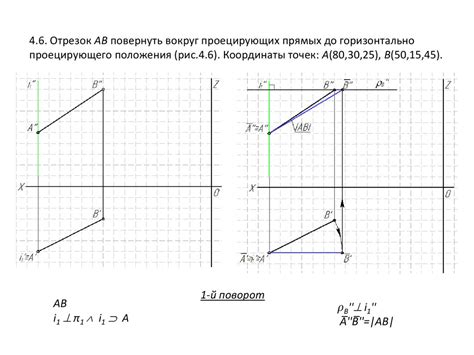
Прямые уровня, также известные как нивелиры, позволяют строителям с легкостью определить горизонтальные и вертикальные плоскости. Они оснащены точкой установки и встроенным уровнем, позволяющим строителю выставить идеальный уровень поверхности. Прямые уровня важны при укладке фундамента, пола, стен и потолков в зданиях.
Проецирующие прямые, также называемые рейками, используются для создания горизонтальных плоскостей при строительстве, особенно на больших расстояниях. Они состоят из линейных элементов, обеспечивающих прямую и ровную поверхность. Проецирующие прямые часто применяются при строительстве дорог, аэропортов, мостов и других проектов, требующих высокой точности и качества работы.
Роль прямых уровня и проецирующих прямых в строительстве состоит в том, чтобы обеспечить точность и правильность установки элементов конструкции. Они помогают минимизировать ошибки и искривления, которые могут возникнуть в процессе строительства. Благодаря прямым уровням и проецирующим прямым строители могут достичь высокой точности и качества в своей работе, обеспечивая прочность и долговечность сооружений.
Все это делает прямые уровни и проецирующие прямые неотъемлемой частью строительного процесса и основными инструментами, необходимыми для достижения оптимальных результатов. Использование этих инструментов помогает строителям создавать надежные и качественные здания, способные выдерживать различные воздействия времени и природных факторов.
Использование прямых уровня и проецирующих прямых в геодезии
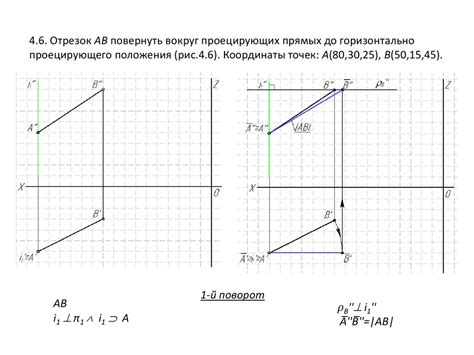
Прямая уровня представляет собой линию, проходящую через две точки и параллельную горизонту. Используя специальный прибор - нивелир, геодезист определяет различия в высотах двух точек на местности. Эта информация позволяет строить высотные карты, определять неровности местности и проектировать инженерные сооружения.
Проецирующая прямая, или геодезическая линия, является кратчайшим расстоянием между двумя точками на поверхности Земли. Ее использование особенно важно для глобальных измерений и картографии. Например, при определении координат точек на поверхности Земли с использованием системы GPS, проецирующие прямые используются для вычисления долготы и широты точек.
Прямые уровня и проецирующие прямые также находят применение при строительстве дорог, железных дорог, тоннелей и других объектов инфраструктуры. Они позволяют определить оптимальные трассы и профили для проектирования и строительства этих сооружений.



