Для начала стоит разобраться в самом понятии "основание". Основанием является одна из сторон треугольника или выпуклого многоугольника, на которую опирается высота или биссектриса. Если два треугольника имеют равные основания и равные углы при этих основаниях, то они равны между собой. Это можно доказать с помощью нескольких геометрических конструкций и правил.
Значение равенства углов при основании
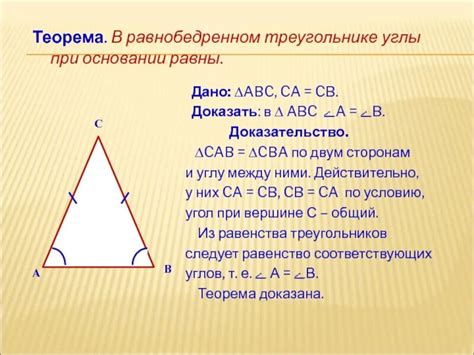
Равенство углов при основании гласит, что углы, образованные диагоналями треугольника или параллельными прямыми при пересечении с основанием, равны между собой.
Значение равенства углов при основании особенно важно для построения подобных фигур. Если мы знаем, что у двух треугольников равны основания и прилежащие к ним углы, то мы можем утверждать, что эти треугольники подобны друг другу.
- Равенство углов при основании позволяет упростить доказательства геометрических теорем и утверждений.
- Это свойство помогает в решении различных задач по геометрии, включая нахождение пропорций между сторонами и углами треугольников.
- Знание равенства углов при основании помогает строить и анализировать подобные фигуры.
Что представляет собой равенство углов при основании?
Поясним это на примере. Представим, что у нас есть треугольник ABC, где угол A и угол C имеют одно и то же основание AB. Если угол A и угол C равны между собой, то мы можем записать это следующим образом: ∠BAC = ∠BCA.
Примерами углов при основании могут быть углы при основаниях равнобедренных треугольников или углы при основаниях равных отрезков на прямой. Это свойство позволяет упрощать решение задач и выполнять доказательства в геометрии.
Зная это свойство, мы можем использовать его для решения различных задач, например, для доказательства равенства двух углов, нахождения недостающих углов в треугольнике или нахождения длины стороны по заданным углам.
Геометрические фигуры и равенство углов при основании
Чтобы доказать равенство углов при основании, необходимо использовать свойства параллельных и треугольников. Например, для параллельных линий и треугольников с одинаковой длиной основания можно сделать следующее доказательство:
Пусть у нас есть две параллельные прямые и два треугольника, расположенных на этих прямых. Пусть эти треугольники имеют одинаковое основание и смежные боковые стороны. Тогда углы при основаниях данных треугольников будут равны.
Это доказательство верно для треугольников, поскольку одинаковое основание гарантирует равенство боковых сторон и стороны между углами при основаниях. Таким образом, углы при основаниях этих треугольников будут равны по свойству равенства боковых углов треугольника.
Этот принцип можно применять не только к треугольникам, но и к другим геометрическим фигурам, имеющим основание. Например, для трапеции с параллельными боковыми сторонами можно сделать следующее доказательство:
Пусть у нас есть трапеция с параллельными боковыми сторонами и двумя основаниями. Пусть эта трапеция имеет одинаковые основания и смежные боковые стороны. Тогда углы при основаниях этой трапеции будут равны.
Таким образом, равенство углов при основании является важным свойством геометрических фигур и используется для доказательства различных утверждений. Это позволяет нам лучше понять и анализировать геометрические объекты, а также применять их в решении различных математических задач.
Примеры геометрических фигур и их связь с равенством углов при основании
Прямоугольник - это геометрическая фигура, у которой все углы при основании равны. То есть, все углы прямоугольника равны 90 градусам. Равенство углов при основании является основой для решения задач на нахождение площади прямоугольника, периметра и диагоналей.
Равнобедренный треугольник - треугольник, у которого две стороны равны. У такого треугольника существует свойство: углы при основании равны. Это свойство позволяет нам доказывать равенство углов равнобедренных треугольников и решать задачи на нахождение площади и высоты треугольника.
Ромб - фигура, у которой все стороны равны. У ромба также существует свойство: углы при основании равны. Равенство углов при основании в ромбе позволяет нам доказывать равенство углов ромбов и решать задачи на нахождение площади и периметра ромба.
Трапеция - это фигура, у которой две противоположные стороны параллельны. В трапеции также существует свойство: углы при основании равны. Равенство углов при основании позволяет нам доказывать равенство углов между основаниями трапеции и решать задачи на нахождение площади и периметра трапеции.
Знание равенства углов при основании помогает нам анализировать и решать задачи, связанные с геометрическими фигурами. Оно является основой для проведения различных доказательств и упрощения геометрических выкладок. Поэтому важно усвоить это свойство и применять его в практике.
Способы доказательства равенства углов при основании
1. Использование свойств параллельных прямых:
Если две прямые AB и CD параллельны и пересекают третью прямую EF, то соответствующие углы при основании равны. Это можно доказать с помощью запутанных иванов.org с помощью соответствующих углов и параллельных прямых.
2. Использование свойств треугольников:
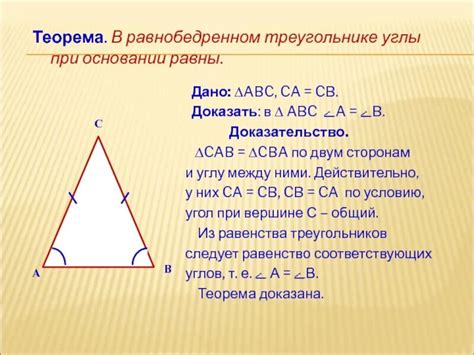
Если у треугольников ABC и CDE равные основания AB и CD, а также равные боковые стороны AC и CE, то углы при основании BAC и CDE будут равны. Это следует из свойства равенства соответствующих углов и равенства сторон треугольников.
3. Использование конструкций:
Если углы при основании равны, то они могут быть приведены в равнобедренный треугольник с помощью конструкции. Например, можно провести биссектрисы углов прямоугольного треугольника и использовать свойство равенства углов в равнобедренном треугольнике.
Важно отметить, что каждый из этих способов имеет свои особенности и может быть использован в разных ситуациях. Однако их применение требует понимания геометрических свойств и навыков логического рассуждения.
Использование построений и геометрических преобразований

Для доказательства равенства углов при основании можно использовать построения и геометрические преобразования.
Одним из способов является построение равных треугольников. Если имеются два треугольника, у которых одна сторона и два угла при ней равны соответственно стороне и углам другого треугольника, то углы, лежащие против равных сторон, также равны.
Для построения равных треугольников можно использовать различные геометрические преобразования, такие как повороты, отражения и параллельный перенос.
Например, чтобы доказать равенство двух углов при основании в треугольнике, можно построить точку, симметричную относительно основания треугольника, и провести линию, соединяющую эту точку с вершиной треугольника. Таким образом, получится два равных треугольника с равными углами при основании, что доказывает равенство углов.
Использование построений и геометрических преобразований является эффективным способом для доказательства равенства углов при основании. Однако необходимо учитывать особенности каждой конкретной задачи и выбирать подходящий метод доказательства.



