Пропорция - один из ключевых понятий в алгебре и математике в целом. Она представляет собой равенство двух отношений и широко используется для решения различных задач, как в школьном курсе, так и в реальной жизни. Пропорция имеет важное значение не только в алгебре, но и в других науках, таких как физика, химия и экономика.
Пропорциональные отношения можно найти практически во всех сферах нашей жизни, например, при расчете количества ингредиентов при приготовлении пищи или при определении времени, необходимого для преодоления определенного расстояния. Пропорции позволяют нам установить связь между разными величинами и найти неизвестные значения.
В алгебре пропорция представляет собой равенство двух дробей. Обычно пропорцию записывают в виде a/b = c/d, где a, b, c и d - числа. Значения a и d называются крайними членами пропорции, а значения b и c - средними членами. Равенство пропорции означает, что отношение между крайними членами равно отношению между средними членами.
Определение пропорции в алгебре

Пропорция записывается в следующем виде:
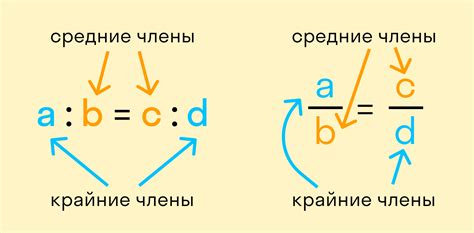
- a : b = c : d
- a/b = c/d
Здесь a, b, c и d – это числа, которые составляют пропорцию. В пропорции a и d называются крайними, а b и c называются средними. Крайние члены и средние члены пропорции обладают свойством: произведение крайних членов равно произведению средних членов.
Пропорции широко используются для решения различных задач в алгебре и геометрии. Они помогают сравнивать значения, искать неизвестные величины, а также решать уравнения и находить значения переменных.
Пропорции имеют важное значение в ряде математических концепций и моделей, таких как пропорциональность, подобие фигур, гармонические отношения и другие. Поэтому понимание и умение работать с пропорциями являются важными навыками в алгебре.
Свойства пропорций в алгебре
Вот некоторые из основных свойств пропорций:
- Свойство признака пропорциональности: если в пропорции два отношения равны, то они пропорциональны. То есть, если $a:b = c:d$, то $a/b = c/d$.
- Свойство сокращения: если в пропорции можно сократить одинаковые множители, то их можно сократить. Например, если $a:b = 2c:2d$, то $a/b = c/d$.
- Свойство расширения: если в пропорции одно отношение равно нулю, то и другое отношение должно быть равно нулю. То есть, если $a:b = 0:c$, то $a = 0$ или $c = 0$.
- Свойство равноточия: если в пропорции два отношения равны, то и их обратные отношения также равны. То есть, если $a:b = c:d$, то $b/a = d/c$.
- Свойство сумма-произведение: в пропорции сумма крайних и средних членов равна произведению крайних членов. То есть, если $a:b = c:d$, то $a+d = b+c$.
Знание и применение этих свойств позволяет эффективно решать задачи, связанные с пропорциями в алгебре. Регулярная практика поможет закрепить материал и сделать процесс решения задач быстрее и точнее.
Применение пропорций в алгебре

Например, пропорции используются для решения задач по подобию фигур. Если две фигуры подобны, то соответствующие стороны этих фигур образуют пропорцию. При использовании пропорций можно находить значения неизвестных сторон или углов.
Кроме того, пропорции широко применяются в смешанных и обратных пропорциях.
- В смешанной пропорции даны два отношения и одно из них выражается через неизвестное значение. Методика решения заключается в нахождении неизвестного значения, используя свойства пропорций.
- В обратной пропорции одно отношение является обратным к другому, то есть их произведение равно единице. Обратные отношения могут использоваться для нахождения неизвестных значений при известных пропорционных отношениях.
Таким образом, пропорции играют важную роль в алгебре, позволяя решать разнообразные задачи по подобию фигур, смешанным и обратным пропорциям. Знание и умение применять пропорции позволяют более эффективно решать алгебраические задачи и получать точные результаты.
Решение задач с использованием пропорций в алгебре

Для решения задач с использованием пропорций, необходимо уметь составлять и анализировать пропорции, а также применять правила и свойства пропорций. Рассмотрим одну из типичных задач для школьной программы.
Пример задачи:
Мария прошла 4 километра за 1 час. Сколько времени ей понадобится, чтобы пройти 10 километров?
Решение:
Дана пропорция: 4 километра --- 1 час = 10 километров --- х часов.
Чтобы решить эту пропорцию, нужно применить правило трех: умножить количество километров на время и поделить на известное количество километров:
4 * 10 / 1 = 40 / 1 = 40
Таким образом, Марии понадобится 40 часов, чтобы пройти 10 километров.
Основное правило при решении задач с пропорциями - сохранение отношений между величинами. Правила и свойства пропорций помогают легко и эффективно решать задачи разной сложности.
Примеры из учебника по алгебре 7 класса

Пример 1:
- Дана пропорция: a/b = c/d
- Нужно найти значение одной из переменных.
- Решение: умножаем крест-накрест: a*d = b*c
Пример 2:
- Дана пропорция: a/b = c/d
- Известно значение одной из переменных.
- Нужно найти значение другой переменной.
- Решение: умножаем значение известной переменной на противоположное значение переменной, которую нужно найти, и делим на значение противоположной переменной: a = (b*c)/d
Пример 3:
- Дана пропорция: a/b = c/d и известны значения двух переменных.
- Нужно найти значение оставшейся переменной.
- Решение: умножаем значение известных переменных и делим на значение переменной, которую нужно найти: d = (b*c)/a
Пропорции широко применяются в математике и реальной жизни для решения различных задач, таких как расчеты, соотношения и пропорциональные зависимости.



