Пропорциональность чисел в геометрии является одним из основополагающих понятий, позволяющих понять взаимосвязь между геометрическими объектами. В геометрии пропорциональность может быть найдена в различных аспектах, начиная от простейших геометрических фигур и заканчивая сложными конструкциями.
Определение пропорциональности можно сформулировать следующим образом: два набора чисел являются пропорциональными, если они представляют отношения длин сторон или площадей геометрических объектов, и эти отношения остаются неизменными при изменении размеров объектов.
Примером пропорциональности чисел в геометрии может служить отношение длин сторон прямоугольника. Если длина и ширина прямоугольника увеличиваются в одно и то же количество раз, то отношение длин сторон остается неизменным и прямоугольник сохраняет свою пропорциональность.
Пропорциональность чисел в геометрии: определение и примеры
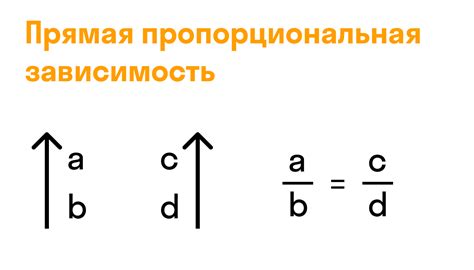
Например, рассмотрим треугольники ABC и XYZ. Если отношение длин сторон AB и XY равно отношению длин сторон AC и XZ, то эти треугольники пропорциональны. В этом случае можно утверждать, что треугольник ABC похож на треугольник XYZ по форме.
Другим примером пропорциональности чисел в геометрии является понятие "подобие". Два многоугольника называются подобными, если все их углы равны между собой и отношение длин соответствующих сторон постоянно. Например, если отношение длин сторон двух треугольников ABC и XYZ равно, то можно сказать, что эти треугольники подобны.
Пропорциональность чисел в геометрии играет важную роль при решении задач, построении и анализе фигур. Она позволяет сравнивать и классифицировать геометрические объекты, а также делает возможным применение подобия и пропорций для нахождения неизвестных длин, площадей и объемов в сложных геометрических конструкциях.
Что такое пропорциональность чисел?

В пропорциональности чисел сравниваются отношения между различными числами. Если две пары чисел имеют одинаковые отношения, они считаются пропорциональными. Например, если отношение между числами 2 и 4 равно отношению между числами 6 и 12, то эти числа пропорциональны.
Пропорциональность чисел может применяться в различных ситуациях геометрии, например:
- При расчетах масштабного соотношения в картографии и графике.
- При нахождении соответствующих длин сторон в подобных фигурах.
- При определении соотношения площадей и объемов фигур.
В геометрических задачах пропорциональность чисел может служить основой для решения сложных задач, так как позволяет установить связь между числами и их геометрическими характеристиками. Понимание пропорциональности и ее применение в геометрии является важным навыком для учеников и студентов, которые изучают эту область науки.
Примеры пропорциональности в геометрии
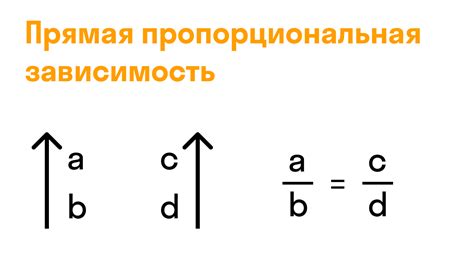
Пропорциональность чисел в геометрии играет важную роль при решении различных задач на плоскости и в пространстве. Пропорция означает равенство отношений между четырьмя числами или величинами.
Рассмотрим несколько примеров пропорциональности в геометрии:
| Пример | Описание |
|---|---|
| 1 | Длины сторон подобных треугольников |
| 2 | Площади подобных треугольников |
| 3 | Объемы подобных тел |
| 4 | Отношение площадей двух подобных фигур |
В каждом из этих примеров числа или величины имеют постоянное отношение друг к другу. Например, в случае подобных треугольников, длины их сторон пропорциональны, то есть соотношение длин сторон одного треугольника к длинам сторон другого треугольника будет всегда одинаковым.
Пропорциональность чисел в геометрии помогает установить связь между различными геометрическими объектами и использовать эти связи для решения задач и построения различных формул и теорем.
Как определить пропорциональность чисел в геометрии?
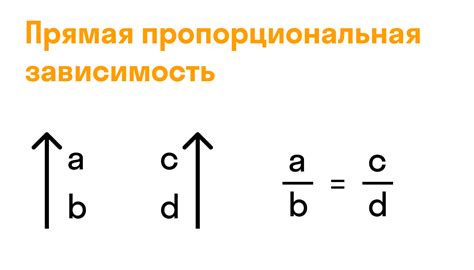
Чтобы определить пропорциональность чисел в геометрии, необходимо выполнить следующие шаги:
- Рассмотреть заданную геометрическую фигуру и определить, какие элементы и числа в ней связаны.
- Составить отношение между элементами, используя числа. Например, если речь идет о треугольнике, можно использовать отношение длины стороны к длине другой стороны или отношение площади к площади.
- Сравнить полученные отношения и проверить, являются ли они постоянными или изменяются в зависимости от выбранной пары чисел.
Если отношение между числами остается неизменным при изменении выбора пары чисел, то можно сказать, что числа пропорциональны. В противном случае, числа не являются пропорциональными.
Пропорциональность чисел в геометрии имеет широкий спектр применений. Она позволяет выявлять и анализировать закономерности в геометрических фигурах, а также использовать их для решения различных задач в математике и инженерии.
Свойства пропорциональных чисел в геометрии

Пропорциональные числа в геометрии играют ключевую роль при решении множества задач. Они определяются отношением между двумя или более числами, которые сохраняют одну и ту же пропорцию при изменении своих значений.
В геометрии, пропорциональные числа используются для описания отношения между длинами, площадями и объемами фигур. Знание свойств пропорциональных чисел помогает решать задачи, связанные с подобием фигур, расчетом пропорциональных сторон и нахождением недостающих параметров.
Основные свойства пропорциональных чисел в геометрии:
- Сохранение пропорциональности при умножении и делении: Если четыре числа a, b, c и d образуют пропорцию, то их произведения a*b и c*d тоже образуют пропорцию. Аналогично, если a*b и c*d образуют пропорцию, то a, b, c и d также образуют пропорцию.
- Сохранение пропорциональности при сложении и вычитании: Если четыре числа a, b, c и d образуют пропорцию, то их сумма a+b и разность c-d также образуют пропорцию. В обратном случае, если a+b и c-d образуют пропорцию, то a, b, c и d также образуют пропорцию.
- Поменять местами числа: Если a/b = c/d, то можно поменять местами числа и получить b/a = d/c. Это свойство можно использовать для удобства расчетов и облегчения работы с пропорциями.
Соблюдение данных свойств помогает упростить геометрические расчеты и искать закономерности в отношениях между числами. Понимание пропорциональных чисел позволяет строить логическую цепочку для решения сложных геометрических задач и упростить процесс нахождения решений.
Как использовать пропорциональность чисел в геометрии?
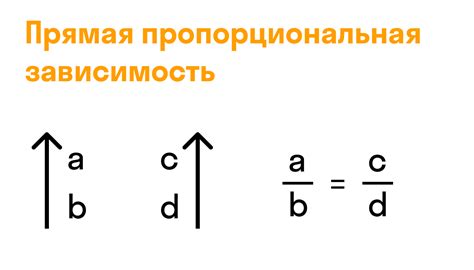
1. Решение подобия треугольников: Если две треугольника подобны, то соответствующие их стороны пропорциональны. Это значит, что отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника остается постоянным. Используя эту пропорциональность, можно находить пропущенные стороны или вычислять площади треугольников.
2. Разделение отрезка: Пропорциональность чисел позволяет разделять отрезки на определенные отношения. Например, если отрезок AB делится внутри на отрезки AC и CB так, что отношение длин AC к CB равно отношению длин AB к AC, то говорят, что точка C делит отрезок AB внутренним пополам. Это свойство применяется, например, при построении прямоугольников и делении отрезков в заданных соотношениях.
3. Расчет площадей: Площадь многоугольника или сложной фигуры можно вычислить, используя пропорциональность отрезков или сторон. Например, если у нас есть две прямоугольные треугольники с общим углом, то отношение их катетов будет равно отношению их площадей.
4. Решение задач на подобие и пропорции: В геометрии часто возникают задачи на подобие фигур и пропорциональность их сторон. Решая такие задачи, необходимо использовать пропорциональность чисел, чтобы найти неизвестное значение или пропущенную сторону.
Все эти примеры показывают, что пропорциональность чисел является важным инструментом для анализа и решения разнообразных геометрических задач. Понимание и умение использовать пропорциональность чисел поможет вам в решении задач, связанных с геометрией и соотношением размеров в различных фигурах.
Пропорциональность чисел и соотношение сторон в геометрии
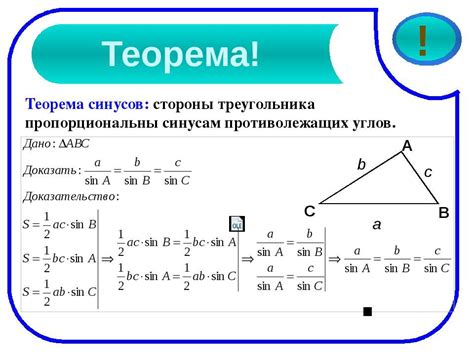
Пропорциональность чисел в геометрии применяется, например, при решении задач о пропорциональности сторон многоугольников. Если у двух многоугольников соответствующие стороны пропорциональны, то говорят, что у этих многоугольников имеется подобие. Другими словами, многоугольники похожи друг на друга, но могут иметь разный масштаб.
Для пропорциональных сторон в геометрии можно записать соотношение в виде:
a/b = c/d
где a и b – длины соответствующих сторон одного многоугольника, а c и d – длины соответствующих сторон другого многоугольника. Это соотношение позволяет определить, насколько один многоугольник подобен другому.
Примером пропорциональности чисел в геометрии может служить соотношение сторон равнобедренного треугольника. У равнобедренного треугольника две стороны равны, а третья сторона – основание – отличается от них. Между длинами сторон равнобедренного треугольника всегда существует пропорция, которая позволяет определить их отношение.
Таким образом, пропорциональность чисел в геометрии является базовым понятием при изучении соотношения сторон геометрических фигур. Она позволяет определять подобие фигур, а также решать задачи, связанные с изменением масштабов фигур.
Закономерности пропорциональности чисел в геометрии

Пропорциональность чисел в геометрии подразумевает, что если два отношения (доли или дроби) между четырьмя числами равны, то они называются пропорциональными. В контексте геометрии это означает, что длины сторон или отрезков могут быть выражены в виде пропорции, что позволяет определить связь между различными элементами фигур.
Пропорциональность чисел в геометрии характеризуется также существованием "золотого сечения", которое является особой математической константой. Золотое сечение имеет значение приблизительно равное 1,618 и выражает идеальное пропорциональное соотношение между двумя отрезками, при котором отношение меньшей части к большей равно отношению большей части ко всему отрезку.
Закономерности пропорциональности чисел в геометрии не только помогают визуально согласовывать элементы фигур с их окружением, но также имеют значительное эстетическое значение. Пропорциональные соотношения используются в дизайне, искусстве и архитектуре для создания гармоничных и привлекательных композиций.
Применение пропорциональности чисел в геометрии на практике

Пропорциональность чисел играет важную роль в геометрии и на практике используется для решения различных задач и построения геометрических фигур. Вот несколько примеров, которые иллюстрируют применение пропорциональности в геометрии:
1. Подобные фигуры. Если две фигуры подобны, то соответствующие стороны их подобными треугольниками будут пропорциональны. Например, если два треугольника подобны, то отношения длин их сторон будут равны.
2. Подобие треугольников. Если имеется треугольник, который описывает большую фигуру, и треугольник, который описывает меньшую фигуру, то отношение длин сторон этих треугольников будет равно отношению площадей большей и меньшей фигур.
3. Пропорциональные отрезки. Если имеется отрезок AB, который делится точкой C в определенном отношении, то отношение длин отрезков AC и CB будет равно отношению длин AB и CD. Это свойство используется при построении различных геометрических фигур и определении их размеров.
4. Углы. В некоторых геометрических фигурах, таких как параллелограммы и треугольники, пропорциональность используется для определения значений углов. Например, в треугольнике ABC, известное отношение сторон AB и BC может использоваться для определения соответствующего угла ACB.
Пропорциональность чисел играет фундаментальную роль в геометрии, позволяя нам анализировать и определять размеры и отношения в различных геометрических фигурах. Это является неотъемлемой частью математического аппарата, используемого геометрами в решении задач и построении фигур.



