Производная функции является одной из основных понятий математического анализа. Она позволяет вычислять скорость изменения функции в каждой точке её области определения. Изучение производных функций является важным этапом в обучении математике и имеет множество практических применений в физике, экономике и других областях науки.
Рассмотрим функцию y = cos(2x), где cos - это тригонометрическая функция косинуса, а 2x - аргумент функции. Мы хотим найти производную этой функции, то есть выразить её скорость изменения в каждой точке x.
Для вычисления производной функции y = cos(2x) применяется правило взятия производной сложной функции. Согласно этому правилу, производная сложной функции равна произведению производной внешней функции на производную внутренней функции, взятую в точке аргумента внутренней функции.
Значение производной функции y = cos(2x)
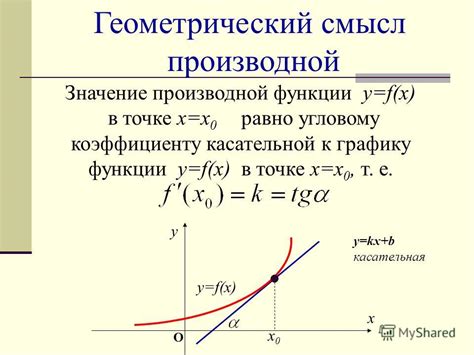
Производная функции позволяет нам определить изменение значения функции в зависимости от изменения ее аргумента. В данном случае, нам необходимо найти производную функции y = cos(2x).
Для взятия производной функции cos(2x) мы можем использовать формулу производной для композиции функций:
- Производная функции cos(x) равна -sin(x).
- Производная функции 2x равна 2.
Исходя из этой формулы, мы можем найти производную функции y = cos(2x):
- Производная функции cos(x) равна -sin(x), поэтому производная функции cos(2x) будет равна -sin(2x).
- Производная функции 2x равна 2, поэтому производная функции cos(2x) будет умножена на 2, то есть 2(-sin(2x)).
Итак, производная функции y = cos(2x) будет равна -2sin(2x).
Определение производной

Пусть у нас есть функция y = f(x), где x – независимая переменная, а y – зависимая переменная. По определению, производная функции f(x) в точке x = a определяется следующим образом:
limh→0 (f(a+h) - f(a))/h
В данном определении h – это бесконечно малое изменение аргумента x. Величина (f(a+h) - f(a))/h называется приращением функции.
Производная функции показывает степень изменения функции в данной точке. Если производная положительна, то это означает, что функция возрастает в данной точке. Если производная отрицательна, то функция убывает в этой точке. Если производная равна нулю, то это может указывать на экстремум функции – минимум или максимум.
Определение производной дает возможность более точно изучать функции и их поведение в разных точках. Она используется во многих областях, включая физику, экономику, статистику и другие науки.
Функция y = cos 2x
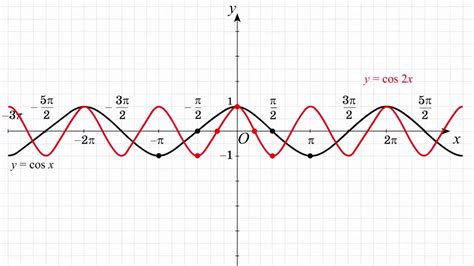
В данной функции, производная может быть найдена с помощью правила взятия производной для функции cos x.
Правило взятия производной cos x гласит: если y = cos x, то производная функции y по переменной x равна -sin x.
Применяя это правило к функции y = cos 2x, получаем, что производная функции y по переменной x равна -sin 2x.
Таким образом, производная функции y = cos 2x равна -sin 2x.
Значение производной
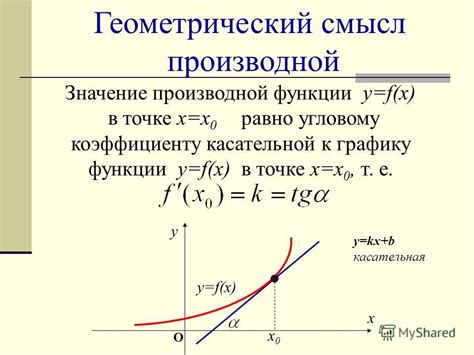
Производная функции y = cos(2x) показывает скорость изменения функции в каждой точке. Для нахождения производной данной функции используется правило дифференцирования, полученное на основе обратной функции синуса:
dy/dx = -2sin(2x)
Значение производной позволяет определить наклон касательной линии к графику функции в каждой точке. Если значение производной положительно в конкретной точке, то функция возрастает в данной точке. В случае, если значение производной отрицательно, функция убывает в данной точке. Если же значение производной равно нулю, то функция имеет экстремум (максимум или минимум) в данной точке.
Знание значения производной позволяет анализировать поведение функции и строить её график. Также оно является основой для решения различных задач оптимизации и определения экстремумов.
Правило взятия производной

Для нахождения производной функции существуют определенные правила. Одно из таких правил - правило взятия производной функции, состоящей из суммы двух или более функций.
Правило взятия производной гласит, что производная суммы функций равна сумме производных этих функций. Формально это можно записать следующим образом:
d/dx(f(x) + g(x)) = f'(x) + g'(x)
где f(x) и g(x) - две функции, f'(x) и g'(x) - их производные по переменной x.
Применение данного правила упрощает процесс нахождения производных сложных функций и позволяет свести задачу к нахождению производных более простых функций.
Производная функции y = cos 2x

Правило взятия производной функции cos(x) гласит:
| Функция | Производная |
|---|---|
| cos(x) | -sin(x) |
Применяя это правило для функции y = cos 2x, мы получаем:
| Функция | Производная |
|---|---|
| cos 2x | -2sin 2x |
Таким образом, производная функции y = cos 2x равна -2sin 2x. Это означает, что скорость изменения графика в каждой точке равна произведению -2 и sin 2x.
Применение производной
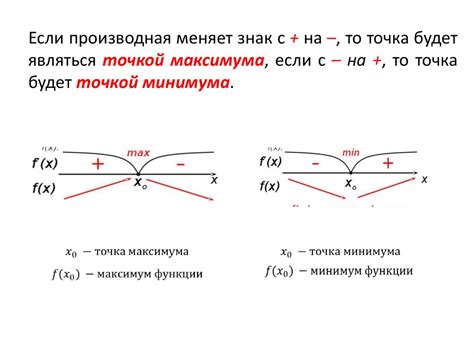
Одним из основных применений производной функции является нахождение экстремумов. Экстремумы представляют собой максимумы и минимумы функций, которые могут быть использованы в оптимизации задач для нахождения наилучшего решения. Производная функции позволяет определить значения x, при которых функция достигает экстремума.
Другим важным применением производной является анализ скорости изменения функции. Производная позволяет определить, насколько быстро функция меняется в заданной точке. Это может быть полезно, например, при анализе роста населения, скорости движения тела или изменения температуры.
Также производная функции может использоваться для определения выпуклости и вогнутости графика функции. Вогнутость и выпуклость функции могут быть важными при анализе теории оптимизации и определении точек перегиба функции.
Производная функции также может быть применена для решения задач из финансовой математики, таких как определение ставки доходности или оценка риска.
Важно отметить, что производная функции может использоваться для решения более сложных математических задач. Например, она может быть использована для нахождения векторов нормали или для анализа кривизны графика функции.
| Область | Пример |
|---|---|
| Оптимизация | Нахождение максимума и минимума функции |
| Физика | Анализ скорости изменения и движения тела |
| Финансы | Оценка ставки доходности и риска |
| Геометрия | Анализ выпуклости и вогнутости графика функции |
Примеры вычисления производной

Рассмотрим функцию y = cos(2x) и найдем ее производную.
Используя правило взятия производной функции cos(x), получаем:
y' = -sin(2x) * 2
Таким образом, производная функции y = cos(2x) равна y' = -2sin(2x).
Для наглядности, рассмотрим несколько примеров вычисления производной:
1. Пример:
Пусть x = 0.
Тогда: y = cos(2 * 0) = cos(0) = 1.
Вычислим производную: y' = -2sin(2 * 0) = 0.
Таким образом, при x = 0 производная функции y = cos(2x) равна нулю.
2. Пример:
Пусть x = π/4.
Тогда: y = cos(2 * π/4) = cos(π/2) = 0.
Вычислим производную: y' = -2sin(2 * π/4) = -2sin(π/2) = -2 * 1 = -2.
Таким образом, при x = π/4 производная функции y = cos(2x) равна -2.
Таким образом, вычислили производную функции y = cos(2x) и рассмотрели примеры ее вычисления.



