Проекция вектора силы на ось – важное понятие в физике, которое позволяет определить, какая часть вектора направлена вдоль выбранной оси. Такой расчет позволяет более точно определить влияние векторной силы на объект или систему.
Для численного расчета проекции вектора силы на ось необходимо знать значение вектора силы и угол между вектором и осью. Для этого можно использовать тригонометрические функции, такие как синус и косинус, которые помогут вычислить проекцию.
Проекция вектора силы на ось может быть положительной или отрицательной, в зависимости от направления и угла между вектором и осью. Важно учитывать знак проекции при дальнейших расчетах, чтобы правильно оценить воздействие силы на объект или систему.
Численный расчет проекции вектора силы на ось является важной задачей в физике и науке, позволяющей более точно предсказывать и анализировать различные физические процессы и явления.
Переопределение векторной проекции

Переопределение векторной проекции – это процесс изменения направления комбинирующего вектора, в результате которого изменяется проекция исходного вектора.
Для переопределения векторной проекции существует несколько методов:
- Метод вращения – основан на повороте комбинирующего вектора относительно исходного вектора;
- Метод растяжения – основан на изменении длины комбинирующего вектора;
- Метод отражения – основан на отразительном отображении комбинирующего вектора.
Каждый из этих методов может быть применен в различных ситуациях, в зависимости от требуемого результата и условий задачи.
Переопределение векторной проекции является важным инструментом в численных расчетах проекции вектора силы на ось. При его использовании можно получить точные значения проекций исходного вектора силы на оси в трехмерном пространстве.
Использование численного метода
Для расчета проекции вектора силы на ось с помощью метода Гаусса необходимо выполнить следующие шаги:
- Задать начальное значение вектора силы и его направление.
- Выбрать ось, на которую будет проецироваться вектор силы.
- Вычислить проекцию вектора силы на выбранную ось, используя формулу проекции.
- Повторить шаги 2-3 для каждой оси, на которую необходимо проецировать вектор силы.
Вычисленные проекции вектора силы на каждую ось могут быть использованы для анализа и управления системой, в которой действует вектор силы. Например, если проекция вектора силы на одну ось больше других, это может указывать на дисбаланс или несоответствие в системе.
Для наглядности результатов расчета можно использовать таблицу, в которой будут представлены значения вектора силы и его проекций на каждую ось:
| Ось | Значение вектора силы | Проекция на ось |
|---|---|---|
| X | ... | ... |
| Y | ... | ... |
| Z | ... | ... |
Таким образом, использование численного метода, такого как метод Гаусса, позволяет рассчитать проекцию вектора силы на ось с высокой точностью и использовать полученные результаты для анализа и управления системой.
Применение алгоритма расчета

Алгоритм расчета проекции вектора силы на ось находит широкое применение в различных областях науки и техники. Он позволяет определить, какая часть вектора силы направлена вдоль заданной оси. Это особенно полезно при решении задач, связанных с применением сил и движением тел.
В механике алгоритм расчета применяется, например, при определении работы силы по перемещению тела вдоль оси. Зная величину вектора силы и угол между вектором силы и осью, можно вычислить работу силы по формуле:
Работа = |F| * cos(угол)
Также алгоритм расчета применяется при определении компонент силы вдоль и поперек осей координат в задачах динамики. Это позволяет разложить вектор силы на две составляющие и установить, какая часть силы направлена вдоль осей X и Y.
В других областях науки также применяются аналогичные алгоритмы расчета проекции вектора силы на оси. Например, в физике алгоритм используется для определения электрического поля вдоль направления движения заряда. В инженерии алгоритм используется, например, при проектировании механизмов и конструкций, чтобы определить, какая часть силы действует на определенную деталь или элемент системы.
Применение алгоритма расчета проекции вектора силы на ось позволяет облегчить решение многих задач, связанных с динамическими процессами и механикой. Это позволяет более точно оценить взаимодействие сил и определить их влияние на объекты и системы.
Моделирование проекции на ось

Моделирование проекции на ось выполняется с помощью применения формулы проекции, которая позволяет определить длину проекции вектора на ось. Для этого необходимо знать длину вектора и угол между вектором и осью, на которую происходит проекция.
Ключевым этапом в моделировании проекции на ось является выбор соответствующей системы координат и оси отсчета. В зависимости от условий задачи можно выбирать как прямоугольную, так и полярную систему координат. При этом ось может быть как осью абсцисс, так и осью ординат или любой другой произвольной осью.
Процесс моделирования проекции на ось можно разделить на следующие шаги:
- Определение вектора силы и оси, на которую будет происходить проекция.
- Вычисление угла между вектором силы и выбранной осью.
- Использование формулы проекции для определения длины проекции вектора на ось.
- Анализ полученных результатов и их использование в дальнейших расчетах.
В процессе моделирования проекции на ось необходимо учитывать особенности задачи и выбирать наиболее подходящую систему координат и оси отсчета. Качественное моделирование проекции на ось позволяет получить точные и надежные результаты численных расчетов.
Выбор координатной системы
Перед тем как приступить к численному расчету проекции вектора силы на ось, необходимо выбрать подходящую координатную систему. Координатная система позволяет задать положение точки в пространстве по определенным координатам.
В задаче на расчет проекции вектора силы на ось, удобно использовать декартову координатную систему. Декартова система состоит из трех взаимно перпендикулярных осей: X, Y и Z.
Плоскости, образованные этими осями, называются плоскостями координат. Ось X показывает направление движения по горизонтали, ось Y - по вертикали, а ось Z - в направлении прямой, формируемой осью X и осью Y.
| Ось | Направление |
|---|---|
| X | Горизонтальное направление |
| Y | Вертикальное направление |
| Z | Прямое направление |
Выбор координатной системы может влиять на удобство расчетов и последующую интерпретацию результатов. Декартова система координат является одной из самых популярных и удобных систем для решения данной задачи.
Оценка результатов расчета

После выполнения численного расчета проекции вектора силы на ось, следует проанализировать полученные результаты и оценить их точность и достоверность.
Также полезным будет провести анализ чувствительности расчета к изменениям входных данных. Если небольшие изменения в величинах силы или угла поворота приводят к значительным изменениям в результате расчета, это может указывать на неправильность метода или ошибку в его реализации.
| Критерий оценки | Результаты расчета | Интерпретация |
|---|---|---|
| Погрешность | Малая разница между ожидаемыми и полученными значениями | Расчет выполнен с высокой точностью |
| Чувствительность | Незначительные изменения входных данных приводят к существенным изменениям в результатах | Метод или его реализация могут содержать ошибки |
| Численная стабильность | Вычисления проходят без существенных изменений значений | Отсутствуют проблемы численного метода |
Анализ точности численного метода
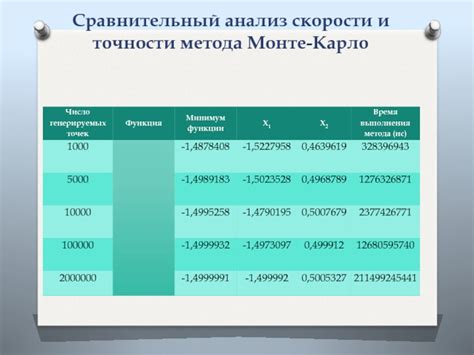
Основным показателем точности численного метода является абсолютная и относительная погрешность. Абсолютная погрешность - это разница между точным значением и вычисленным значением. Она позволяет оценить, насколько близко полученный результат к истинной величине. Относительная погрешность рассчитывается как отношение абсолютной погрешности к точному значению и позволяет оценить, насколько точно численный метод моделирует реальные явления.
Для определения точности численного метода можно также использовать для расчета проекции вектора силы на ось такие критерии как: анализ сходимости метода, проверка сходимости производных в вычисленных точках, сравнение результатов с аналитическими решениями.
Для проведения анализа точности численного метода важно также учесть влияние погрешности входных данных и округления чисел. Например, если входные данные содержат погрешность или вычисления выполняются с ограниченной точностью, то результаты будут содержать соответствующую погрешность.
Таким образом, проведение анализа точности численного метода является важным этапом в разработке численных моделей и позволяет оценить, насколько точно и надежно выполняются вычисления.
Верификация модели проекции

Проверка корректности математической модели проекции осуществляется путем сравнения результатов расчетов с известными значениями. В случае проекции вектора силы на ось, можно выполнить следующие шаги верификации:
- Выбрать известное значение вектора силы и его проекции на ось.
- Использовать математическую модель проекции для расчета проекции вектора силы на ось.
- Сравнить полученный результат с известным значением проекции.
При совпадении результатов можно говорить о корректности модели проекции. Если результаты не совпадают, необходимо провести анализ ошибки и возможные причины ее возникновения. В случае выявления ошибки в модели, необходимо внести соответствующие корректировки и повторить верификацию.
Верификация модели проекции является важным этапом при разработке программного обеспечения, использующего данную модель. Правильная работа проекции вектора силы на ось может быть критически важной во многих приложениях, например, в физических симуляторах или в инженерных расчетах.
Примеры применения численного расчета

Численный расчет применяется во многих областях науки и техники. Ниже приведены несколько примеров его применения.
- Механика. В механике численный расчет используется для моделирования движения различных объектов. Например, можно рассчитать траекторию движения автомобиля, учитывая различные факторы, такие как сила трения, сила сопротивления воздуха и сила гравитации.
- Физика. В физике численный расчет позволяет моделировать поведение частиц в различных физических системах. Например, можно рассчитать траекторию движения планеты вокруг Солнца, учитывая взаимодействие силы притяжения и силы центробежной.
- Инженерия. В инженерии численный расчет необходим для оптимизации конструкций и прогнозирования их поведения в различных условиях. Например, можно рассчитать напряжение в материале при заданной нагрузке и определить его прочность.
- Электротехника. В электротехнике численный расчет используется для моделирования электрических цепей и определения их характеристик. Например, можно рассчитать силу тока и напряжение в различных участках цепи при заданной нагрузке.
- Компьютерные науки. В компьютерных науках численный расчет применяется для решения сложных математических задач и моделирования различных процессов. Например, можно рассчитать оптимальный маршрут для доставки груза, учитывая различные ограничения и условия.
Все эти примеры демонстрируют, как численный расчет позволяет получать точные и надежные результаты, которые могут быть использованы для принятия важных решений и разработки новых технологий.



