Ускорение тела - это величина, характеризующая изменение скорости объекта за единицу времени. В физике, ускорение часто разбивают на составляющие, чтобы лучше понять его поведение в пространстве. Одним из способов представить ускорение является его проекция. Проекция ускорения тела - это составляющая ускорения вдоль выбранной оси или направления.
Проекция ускорения может быть положительной или отрицательной в зависимости от направления ускорения и выбранной системы координат. Если положительное направление оси выбрано в одном направлении, а отрицательное - в противоположном, то ускорение, направленное вдоль оси, будет иметь соответствующую проекцию.
Проекция ускорения тела может быть полезной в различных физических задачах. Например, при движении тела по наклонной плоскости, проекция ускорения вдоль плоскости помогает определить, как сила тяжести разбивается на составляющие, влияющие на движение тела вдоль плоскости и перпендикулярно ей.
Использование проекции ускорения позволяет упростить рассмотрение движения тела и выделить наиболее значимые его характеристики. Поэтому в физике проекция ускорения является важным инструментом для анализа и описания движения объектов в пространстве.
Проекция ускорения тела в физике
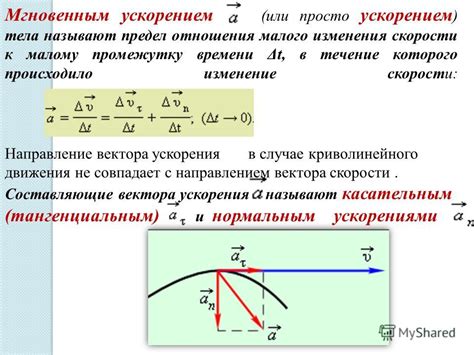
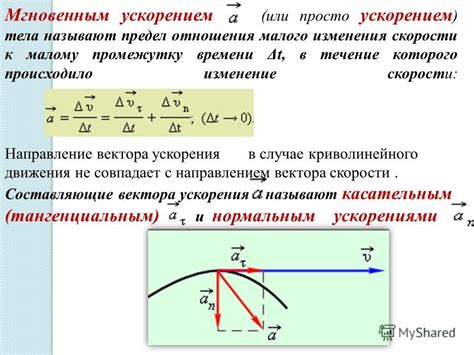
Ускорение – это скорость изменения скорости тела во времени. Однако, ось координат, по которой происходит изменение скорости, может быть любой. Чтобы проиллюстрировать движение тела в определенном направлении, физики используют понятие проекции ускорения.
Проекция ускорения вычисляется путем проектирования вектора ускорения на некоторую ось или плоскость. В результате получается ускорение вдоль этой оси или в плоскости. Ось или плоскость выбираются в соответствии с конкретными условиями задачи и исследуемым движением.
Проекция ускорения тела является важным физическим понятием, которое может применяться в различных областях, таких как механика, астрономия, гидродинамика и другие. Знание проекции ускорения позволяет уточнить представление о движении тела и описать его изменение в определенном направлении.
Определение и сущность проекции ускорения

Когда тело движется в трехмерном пространстве, его ускорение разлагается на три компоненты: проекции ускорений на оси координат. Проекция ускорения по каждой из осей показывает, какое изменение скорости происходит вдоль этой оси. Таким образом, мы можем рассмотреть движение тела в каждом измерении отдельно.
С использованием проекции ускорения можно определить, какие силы воздействуют на тело и как они влияют на его движение. Если проекция ускорения равна нулю по одной из осей, это означает, что тело не подвергается воздействию силы в этом направлении.
Важно понимать, что проекция ускорения зависит от выбранной системы координат. Если система координат вращается или изменяется, проекции ускорения могут изменяться и влиять на движение тела. Поэтому при анализе движения тела необходимо учитывать выбранную систему координат и ее изменение во времени.
Получение и анализ проекции ускорения важны для изучения и описания движения тела в физике. Они позволяют более детально рассмотреть и понять его динамику и физические законы, действующие на тело.
Формула для вычисления проекции ускорения
Формула для вычисления проекции ускорения имеет вид:
где:
aпр - проекция ускорения тела;
a - абсолютное значение ускорения тела;
θ - угол между вектором ускорения и направлением вдоль которого вычисляется проекция ускорения (обычно указывается в радианах).
Данная формула основана на теоретических принципах тригонометрии и векторной алгебры, и позволяет определить проекцию ускорения в любом заданном направлении.
Зависимость проекции ускорения от угла и скорости

При движении тела по закону равномерного прямолинейного движения, проекция ускорения равна нулю, так как скорость тела не изменяется. Однако, при изменении траектории движения или изменении скорости, проекция ускорения становится ненулевой векторной величиной.
Зависимость проекции ускорения от угла и скорости может быть рассмотрена с помощью геометрических методов. Если направление движения тела представляет собой ось Ox, а направление ускорения - ось Oy, то проекция ускорения будет представлять собой боковое смещение точки движения тела относительно оси Ox.
Известно, что проекция ускорения пропорциональна углу между векторами скорости и ускорения. Чем больше угол между этими векторами, тем больше проекция ускорения. При совпадении направления скорости и ускорения, угол между ними равен нулю и проекция ускорения также равна нулю.
Зависимость проекции ускорения от скорости может быть представлена через формулу: aпр = a * sin(α), где aпр - проекция ускорения, a - абсолютное значение ускорения, α - угол между векторами скорости и ускорения.
Таким образом, зависимость проекции ускорения от угла и скорости позволяет определить направление и величину проекции ускорения для конкретного случая движения тела. Это знание является важным для решения различных задач в физике, связанных с динамикой движения.
Примеры из реальной жизни, где проявляется проекция ускорения

- Автомобиль, двигающийся по дороге с поворотами. Когда автомобиль движется по криволинейному пути, его ускорение имеет направление, касательное к траектории движения в каждой точке. Проекция ускорения в этом случае позволяет определить изменение скорости автомобиля по направлению к вынужденному повороту.
- Мяч, брошенный под углом к земной поверхности. Если мяч брошен под углом к горизонту, его ускорение будет иметь горизонтальную и вертикальную компоненты. Горизонтальная компонента ускорения не изменяет горизонтальную составляющую скорости мяча, в то время как вертикальная компонента ускорения будет влиять на его вертикальное перемещение.
- Падение тела с высоты. Когда тело падает с высоты под действием силы тяжести, его ускорение будет направлено вниз. Проекция ускорения позволяет определить изменение скорости тела вдоль вертикальной оси и рассчитать время падения.
- Ракета, запущенная в космос. При запуске ракеты, ее ускорение осуществляется с помощью силы реактивного двигателя. Проекция ускорения в этом случае позволяет определить изменение скорости по направлению к заданной орбите и обеспечить достижение требуемой орбитальной скорости.
Проекция ускорения является важным инструментом для изучения движения объектов в физике и находит применение в различных областях науки и техники.
Связь проекции ускорения с другими физическими величинами

Проекция ускорения тела играет важную роль в физике, так как она позволяет описать изменение скорости тела в определенном направлении. Проекция ускорения определяется через проекцию силы, действующей на тело, и массу данного тела. Она показывает изменение скорости вдоль данного направления в единицу времени.
Одной из ключевых связей проекции ускорения является второй закон Ньютона, который устанавливает, что проекция ускорения прямо пропорциональна проекции силы, действующей на тело, и обратно пропорциональна его массе. Формула, описывающая связь этих величин, выглядит следующим образом: a = F/m, где а - проекция ускорения, F - проекция силы, действующей на тело, m - масса тела.
Также проекция ускорения имеет важное отношение к кинематике. С помощью проекции ускорения можно вычислить изменение скорости тела в определенное время или расстояние. Для этого необходимо умножить проекцию ускорения на время или расстояние.
Более того, проекция ускорения связана с проекцией скорости с помощью производной. Если проекция ускорения постоянна, то проекция скорости возрастает или уменьшается с постоянной скоростью. Если же проекция ускорения меняется со временем, то проекция скорости зависит от интеграла проекции ускорения по времени.
Таким образом, проекция ускорения является важной физической величиной, связанной с другими основными концепциями физики, такими как силы, скорость и время. Понимание связи проекции ускорения с этими величинами помогает строить более точные математические модели и предсказывать движение тел в пространстве.
Применение проекции ускорения в технике и спорте

В технике проекция ускорения широко используется при разработке и тестировании различных механизмов и устройств. Например, при проектировании автомобилей проекция ускорения позволяет оценить и предсказать поведение автомобиля в различных ситуациях на дороге, таких как разгон, торможение или повороты. Используя проекцию ускорения, инженеры могут оптимизировать дизайн автомобиля и улучшить его характеристики для повышения безопасности и комфорта водителя и пассажиров.
В спорте проекция ускорения играет также важную роль. Например, в лыжных гонках или беге на короткие дистанции спортсмены стремятся минимизировать проекцию ускорения, чтобы достичь наивысшей скорости и преодолеть дистанцию быстрее своих соперников. В таких видах спорта техника бега или лыжного хода играет ключевую роль, и спортсмены уделяют особое внимание минимизации своей проекции ускорения, что позволяет им достичь более высоких результатов.
Таким образом, проекция ускорения имеет широкое применение в технике и спорте. Она помогает предсказывать поведение различных механизмов и устройств, а также оптимизировать движение спортсменов для достижения лучших результатов. Понимание проекции ускорения является важным фактором в этих областях и активно используется для создания новых технологий и достижения спортивных побед.



