Проекция скорости - это важное понятие в физике, которое позволяет описать движение тела в пространстве. В терминах проекции скорости мы можем понять, как быстро тело движется в каждом измерении, а именно по осям x, y и z.
Определение проекции скорости состоит в том, что скорость тела может быть разложена на три компоненты: горизонтальную (по оси x), вертикальную (по оси y) и вдоль оси z. Используя этот подход, мы можем учесть все основные виды движения - прямолинейное, криволинейное и вращательное.
Проекция скорости не зависит от ориентации системы координат, поэтому она является удобным инструментом для анализа движения тела. Например, если тело движется по дуге окружности, его горизонтальная и вертикальная проекции скорости будут меняться, но их сумма всегда будет равна общей скорости тела.
Что такое проекция скорости тела в физике?
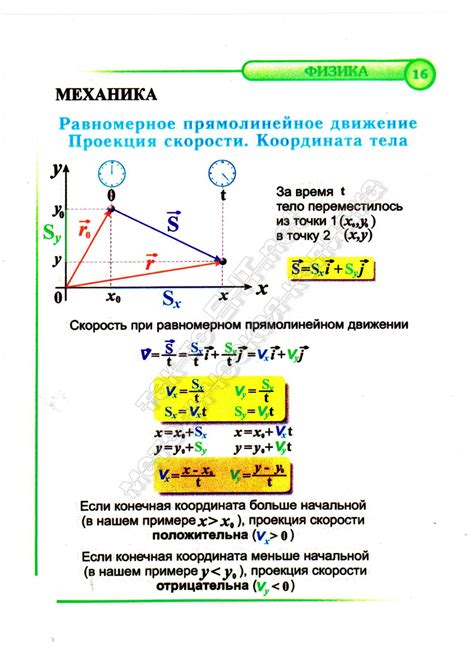
Проекция скорости тела в физике относится к изучению движения объектов в пространстве и времени. Она представляет собой составляющую скорости, направленную вдоль заданной оси. В зависимости от выбранной оси проекция может быть как положительной, так и отрицательной.
Скорость тела - векторная величина, которая описывает изменение позиции объекта в единицу времени. Проекция скорости тела позволяет рассматривать его движение только вдоль определенной оси, что упрощает анализ и вычисления.
Проекция скорости может быть вычислена с использованием простого математического соотношения. Она равна произведению модуля всей скорости на косинус угла между направлением всей скорости и направлением оси, куда проводится проекция.
Примером проекции скорости тела может служить бросок предмета под углом к горизонту. В этом случае горизонтальная проекция скорости будет описывать движение предмета вдоль горизонтальной оси, а вертикальная проекция скорости будет описывать движение предмета вдоль вертикальной оси.
Изучение проекции скорости тела важно для понимания и анализа сложных движений, таких как броски, падения, движение по криволинейным траекториям. Она позволяет выделить и изучить отдельные составляющие движения, что помогает получить более полное представление о его характеристиках и законах.
Важно отметить, что проекция скорости тела не является независимой от векторной скорости величиной, а является ее частью, указывающей направление и интенсивность движения по определенной оси.
Определение и основные понятия
Основные понятия, связанные с проекцией скорости, включают:
- Проекция скорости на ось движения. Это компонента скорости, измеряемая в направлении движения тела.
- Проекция скорости на перпендикулярную ось. Это компонента скорости, измеряемая в направлении, перпендикулярном оси движения.
- Результатантная проекция скорости. Это сумма проекций скорости на оси движения и перпендикулярную ось.
Проекция скорости тела может быть положительной или отрицательной, в зависимости от направления движения. Положительная проекция скорости указывает на движение вперед, а отрицательная - на движение назад.
Например, при вертикальном броске мяча вверх, проекция его скорости на вертикальную ось возрастает, пока мяч движется вверх, а затем уменьшается, пока мяч падает вниз. Проекция скорости на горизонтальную ось остается постоянной, так как горизонтальная скорость не изменяется.
Значение проекции скорости в механике

Зная проекцию скорости, можно значительно упростить анализ движения. Например, при рассмотрении двухмерного движения, можно разложить вектор скорости на две его проекции вдоль осей координат X и Y. Такое разложение позволяет рассматривать движение по отдельности вдоль каждого направления. Таким образом, проекции скорости позволяют сделать анализ движения более простым и понятным.
Проекции скорости часто используются в задачах, связанных с различными видами движения. Например, при рассмотрении движения по окружности можно определить проекцию скорости вдоль радиуса и проекцию скорости вдоль касательной. Это позволяет учесть влияние кривизны траектории на движение тела.
Также проекции скорости могут быть использованы для определения угла между скоростью и определенным направлением. Например, при рассмотрении броска объекта под углом к горизонту можно определить проекцию скорости вдоль горизонтальной оси и проекцию скорости вдоль вертикальной оси. Это позволяет легче анализировать движение тела в вертикальной и горизонтальной плоскостях.
В итоге, проекции скорости в механике играют важную роль, упрощая анализ движения и позволяя более точно определить характеристики движения тела в заданном направлении.
Как рассчитать проекцию скорости тела?
Для расчета проекции скорости тела необходимо знать величину скорости и угол, под которым направлена скорость относительно оси координат.
Проекция скорости тела может быть рассчитана с помощью следующей формулы:
vx = v * cos(θ)
где vx - проекция скорости тела на ось координат, v - величина скорости тела, θ - угол между направлением скорости и осью координат.
Например, если тело движется со скоростью 10 м/с под углом 30 градусов к оси х, то проекция скорости тела на ось х будет:
vx = 10 м/с * cos(30 градусов) ≈ 8.66 м/с
Таким образом, проекция скорости тела на ось х составляет около 8.66 м/с.
Пример проекции скорости при вертикальном движении
При вертикальном движении тела по прямой оси OY его скорость можно представить в виде двух компонент: горизонтальной и вертикальной. Для определения проекций скорости используется теорема Пифагора.
Рассмотрим пример. Пусть тело движется вниз с ускорением 5 м/с², начальная скорость равна 10 м/с и начальная координата равна 0 м. Необходимо определить проекции скорости на горизонтальную и вертикальную оси через 5 секунд после начала движения.
Для начала вычислим вертикальную компоненту скорости (Vу). Используем формулу:
| Vу = V0у + aу * t |
| Vу = 10 м/с + (-5 м/с²) * 5 с = -15 м/с |
Здесь V0у - начальная вертикальная скорость, ау - вертикальное ускорение, t - время. Отрицательное значение скорости говорит о том, что тело движется вниз.
Далее вычислим горизонтальную компоненту скорости (Vх), которая остается постоянной во время вертикального движения. Мы можем записать:
| Vх = V0х = 0 м/с |
Здесь V0х - начальная горизонтальная скорость, которая равна 0 м/с, так как тело движется только по вертикальной оси.
Таким образом, после 5 секунд проекция скорости на горизонтальную ось будет равна 0 м/с, а проекция скорости на вертикальную ось -15 м/с.
Пример проекции скорости при горизонтальном движении
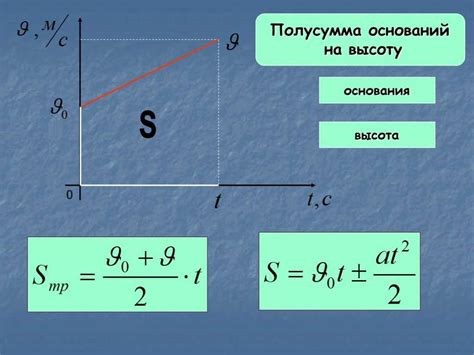
vx = v * cos(α)
где vx – проекция скорости по горизонтали, v – абсолютная величина скорости тела, α – угол между направлением скорости и горизонтом.
Давайте рассмотрим пример. Пусть тело движется со скоростью 10 м/с и угол между направлением этой скорости и горизонтом равен 30°. Чтобы найти проекцию скорости по горизонтали, мы подставим эти значения в формулу:
vx = 10 м/с * cos(30°)
Применяя тригонометрическую функцию к углу, мы найдем:
vx = 10 м/с * 0.866
vx ≈ 8.66 м/с
Таким образом, проекция скорости по горизонтали для этого примера составляет примерно 8.66 м/с.
Проекция скорости тела на наклонной плоскости
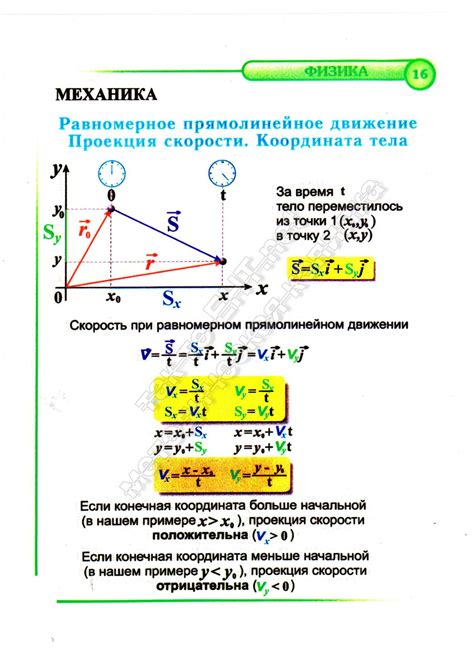
Горизонтальная проекция скорости тела на наклонной плоскости определяет изменение положения тела в горизонтальном направлении. Она определяется как произведение модуля полной скорости тела на наклонной плоскости на косинус угла между направлением движения и горизонтом.
Вертикальная проекция скорости тела на наклонной плоскости характеризует изменение положения тела в вертикальном направлении. Она определяется как произведение модуля полной скорости тела на наклонной плоскости на синус угла между направлением движения и горизонтом.
Для наглядности и удобства решения задач, проекцию скорости тела на наклонную плоскость можно представить в виде таблицы.
| Составляющая скорости | Формула |
|---|---|
| Горизонтальная проекция скорости | Vх = V * cos(α) |
| Вертикальная проекция скорости | Vу = V * sin(α) |
Где V – модуль полной скорости тела на наклонной плоскости, α – угол между направлением движения и горизонтом.
Примером применения проекции скорости тела на наклонной плоскости может быть решение задачи о движении тела по наклонной плоскости. Например, если тело совершает равномерное движение вдоль плоскости под углом к горизонту, то можно использовать проекции скорости для определения его горизонтальной и вертикальной скоростей.
Методы измерения проекции скорости
В физике существует несколько методов измерения проекции скорости тела. Они используются для определения величины и направления скорости движения объекта.
Один из самых распространенных методов измерения проекции скорости - это метод с использованием датчика дистанции. В этом случае используется особый датчик, который может измерять расстояние между объектом и другими пунктами на его пути. Зная изменение расстояния и время, прошедшее между двумя измерениями, можно вычислить проекцию скорости тела.
Еще один распространенный метод измерения проекции скорости - это метод с использованием фотофиниша. В этом случае используется камера, которая фиксирует время прохождения объектом определенного участка пути. Зная длину участка пути и время прохождения, можно вычислить проекцию скорости тела.
Также существует метод измерения проекции скорости с помощью лазерного измерителя дальности. В этом случае лазерный измеритель дальности излучает лазерный луч на объект и фиксирует время отражения лазерного луча. Зная время пути лазерного луча и скорость света, можно вычислить проекцию скорости тела.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода измерения проекции скорости зависит от конкретной задачи и условий эксперимента.



