Проценты – одна из важных математических концепций, которую мы используем в повседневной жизни. Понимание процентов не только помогает нам расширить наши финансовые навыки, но и дает возможность более точно оценивать информацию и принимать обоснованные решения.
Процент – это доля от всего, которая выражается сотыми долями. Когда говорят о процентах, обычно указывают два числа: процентное соотношение и базу. Процентное соотношение показывает, сколько процентов составляет доля от общего числа или количества, а база – это число или количество, относительно которого рассчитывается процент. Например, если на счете в банке лежит 1000 долларов и процентная ставка 5%, то база – 1000 долларов, а процентное соотношение – 5%.
Понимание процентов очень полезно при решении задач из разных областей нашей жизни, таких как финансы, экономика, торговля, математика и т.д. Знание основных формул и правил помогает решать разнообразные задачи, например, вычислять скидки и наценки, расчет процентов повышения или понижения, сравнивать различные ставки и многое другое.
Проценты: основные понятия и формулы

Основные понятия:
База процента – это величина, на которую берется процент. Например, если имеется сумма денег, то базой процента может быть эта сумма.
Процент – это величина, которую берут от базы процента. Например, если берут 10% от суммы денег, то процент равен 10.
Процентная ставка – это отношение процента к базе процента, выраженное в процентах на единицу базы. Например, если 10% берется от суммы денег, то процентная ставка равна 10%.
Процентное выражение – это численное значение процента в виде десятичной дроби или десятичной дроби. Например, 10% равно 0.1 или 10/100.
Основные формулы:
1. Формула процента от числа:
Процент от числа = (число * процент) / 100
2. Формула числа от процента:
Число = (процент от числа * 100) / процент
3. Формула процента от базы:
Процент от базы = (база * процентная ставка) / 100
4. Формула базы от процента:
База = (процент от базы * 100) / процентная ставка
Зная эти понятия и формулы, вы сможете решать различные задачи, связанные с процентами, в финансовых, торговых и повседневных ситуациях.
Что такое процент?

Проценты широко применяются в различных областях, таких как финансы, экономика, математика и торговля. Они помогают нам понять, какую долю составляет одна величина от другой и как изменяется эта доля в разных ситуациях.
Проценты можно рассматривать как десятичные дроби, где 100% равно 1. Например, 50% равно 0,5, а 200% - это 2.
Часто проценты используются для выражения прироста или убытка величины. Например, если товар подорожал на 10%, это означает, что его цена увеличилась на 10% от исходной цены.
Для решения задач с процентами важно знать основные формулы и правила: находить процент от числа, находить число, соответствующее заданному проценту от другого числа, находить процентное отношение и др.
Понимание процентов помогает нам лучше ориентироваться в финансовых вопросах, делать осознанные покупки и выявлять различия в данных и статистике.
Как рассчитывать процент от числа?

Для примера, представим, что необходимо найти 8% от числа 320. Чтобы рассчитать это, нужно перемножить число 320 на 0.08 (8% в десятичном представлении). Результатом будет число 25.6.
Если же вам известно количество процентов, но неизвестно число, от которого нужно найти процент, можно воспользоваться обратной операцией. Для этого необходимо разделить известное количество процентов на десятичное представление процента.
Например, мы знаем, что 20% от числа равно 160. Чтобы найти это число, нужно поделить 160 на 0.2 (20% в десятичном представлении). Получаем число 800.
Помните, что для правильного рассчета процента от числа необходимо всегда приводить проценты к десятичному представлению (делить на 100) и правильно использовать дробные числа в расчетах.
Процентное соотношение чисел: понятие и примеры

Проценты находят широкое применение в различных сферах жизни, таких как финансовые операции, торговля, статистика и даже в повседневных расчетах. Разберем несколько примеров, чтобы лучше понять, как работать с процентным соотношением чисел.
Пример 1: Если цена товара составляет 5000 рублей, а скидка составляет 20%, то какая будет конечная цена товара?
Для начала нужно найти сумму скидки, которая составляет 20% от 5000 рублей: 5000 рублей * 20% = 1000 рублей. Затем нужно вычесть сумму скидки из начальной цены: 5000 рублей - 1000 рублей = 4000 рублей. Итак, конечная цена товара с учетом скидки составляет 4000 рублей.
Пример 2: В компании работает 50 человек, и 30% из них имеют высшее образование. Сколько человек в компании имеют высшее образование?
Для этого нужно найти 30% от 50 человек. Для этого можно использовать формулу: число * процент / 100. Таким образом, 30 * 50 / 100 = 15. Итак, в компании имеется 15 человек с высшим образованием.
Пример 3: В общежитии проживает 120 студентов, и 60% из них являются девушками. Сколько девушек проживает в общежитии?
Для этого нужно найти 60% от 120 студентов. Таким же образом, используя формулу: 60 * 120 / 100 = 72. Итак, в общежитии проживает 72 девушки.
Это лишь несколько примеров, которые помогут вам лучше понять, как работать с процентным соотношением чисел. Зная базовые понятия и используя простые математические операции, вы сможете решать задачи, связанные с процентами, с легкостью.
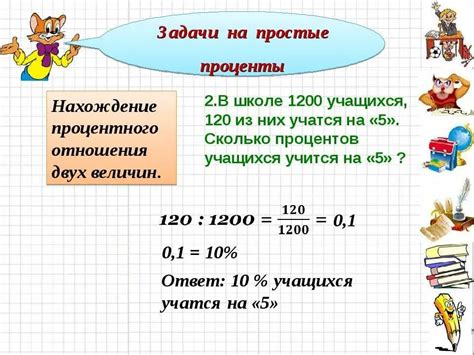
Как решать задачи на нахождение процента от числа?
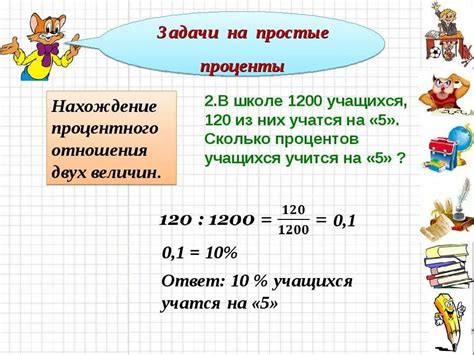
Для начала, необходимо знать формулу для нахождения процента от числа:
процент = число × процент / 100
Как правило, в задачах даны две из трех величин: число, процент и процентная ставка. Остается лишь подставить значения в формулу и выполнить несложные арифметические действия для нахождения ответа.
Например, если нам дано число 200 и процентная ставка 20%, необходимо найти процент от этого числа. Для этого подставим значения в формулу:
процент = 200 × 20 / 100 = 40
Таким образом, 20% от числа 200 равно 40.
Важно обратить внимание на правильное использование процентной ставки в формуле. Если процентная ставка задана в десятичной форме (например, 0,20), необходимо предварительно перевести ее в проценты, умножив на 100. Если процентная ставка задана в виде десятичной дроби (например, 0,2), то результат будет таким же, как и в предыдущем примере.
Иногда в задачах нужно найти исходное число, если известен процент и процентная ставка. Для этого необходимо воспользоваться обратной формулой:
число = процент × 100 / процентная ставка
Например, если нам дан процент 40 и процентная ставка 20%, нужно найти число. Подставим значения в формулу:
число = 40 × 100 / 20 = 200
Таким образом, число, которому соответствует 40% при процентной ставке 20%, равно 200.
Важно помнить, что для успешного решения задач на нахождение процента от числа необходимо правильно понять условие задачи и овладеть навыками работы с простыми арифметическими формулами.
Процентные ставки: виды и расчеты

Существует несколько видов процентных ставок:
- Простые проценты – это ставка, которая начисляется только на начальную сумму. Расчет процентов от начальной суммы производится по формуле:
- Сложные проценты – это ставка, которая начисляется не только на начальную сумму, но и на уже начисленные проценты. Расчет сложных процентов может быть сложнее, но общая формула выглядит следующим образом:
- Эффективная процентная ставка – это ставка, которая учитывает не только номинальную процентную ставку, но и любые дополнительные расходы или доходы, которые могут возникнуть от сделки или инвестиции.
Простые проценты = (Начальная сумма * Процентная ставка * Количество периодов) / 100
Сложные проценты = Начальная сумма * (1 + Процентная ставка / 100) ^ Количество периодов - Начальная сумма
Расчет процентных ставок может быть полезен при планировании личных финансов, выборе оптимальных вариантов кредитования или инвестирования. Понимание различных видов процентных ставок поможет принимать обоснованные решения и избегать финансовых потерь.
Как решать задачи с процентными ставками?

Чтобы решать задачи с процентами, необходимо понять основные понятия и формулы. Основные термины, используемые в задачах с процентами, включают процентную ставку, проценты, начальный капитал, конечный капитал и сумму процентов.
Процентная ставка – это доля (в процентах) от начальной суммы, которую необходимо уплатить или получить в качестве процентов за определенный период времени. Она обозначается символом "%".
Проценты – это денежная сумма, которая уплачивается или получается в результате использования определенной процентной ставки.
Начальный капитал – это сумма денег или других активов, на которую начисляются проценты.
Конечный капитал – это сумма денег или активов, которые получаются после начисления процентов и прибавления их к начальному капиталу.
Сумма процентов – это сумма процентов, которая уплачивается или получается после определенного периода времени.
Чтобы решать задачи с процентами, необходимо использовать различные формулы, такие как формула простых процентов и формула сложных процентов.
Формула простых процентов позволяет рассчитать сумму процентов за определенный период времени, используя процентную ставку и начальный капитал.
Формула сложных процентов позволяет рассчитать конечный капитал, учитывая процентную ставку, начальный капитал и период времени.
Для успешного решения задач с процентными ставками необходимо четко определить известные и неизвестные величины, выбрать подходящую формулу и подставить значения. Важно следить за единицами измерения и правильно интерпретировать результаты.
Следуя этим простым шагам, вы сможете успешно решать задачи с процентами и лучше понимать финансовые процессы, что поможет вам в принятии обоснованных решений, связанных с вашими финансами.
Сложные проценты: что это такое и как решать задачи?

Для решения задач с использованием сложных процентов необходимо знать несколько ключевых понятий:
1. Основная сумма (капитал) – это начальная сумма денег, на которую начисляются проценты.
2. Процентная ставка – это определенный процент от основной суммы, который начисляется на нее.
3. Срок вклада – это период времени, в течение которого осуществляется начисление процентов.
Для расчета суммы с использованием сложных процентов можно использовать формулу:
Сумма = Основная сумма × (1 + Процентная ставка)^Количество периодов
Пример:
У нас есть вклад в банке на 5000 рублей с процентной ставкой 10% в год. Через 3 года мы хотим узнать, сколько денег у нас будет на счету.
Сумма = 5000 × (1 + 0.1)^3 = 5000 × 1.1 × 1.1 × 1.1 = 6655 рублей
Таким образом, через 3 года на счету будет 6655 рублей.
Сложные проценты могут применяться не только для вкладов в банках, но и в других ситуациях, например, при расчете кредитных процентов, инвестициях и долгосрочных финансовых планах.
Важно помнить, что расчет сложных процентов требует точности и внимательности, поэтому рекомендуется использовать калькулятор или специальные программы для автоматического решения задач.
Используя знания о сложных процентах, вы сможете более точно и эффективно планировать свои финансовые операции и прогнозировать будущие доходы или расходы.
Процентные приращения: понятие и способы расчета

Существует несколько способов расчета процентного приращения. Один из них – через разность между новым и старым значением, деленную на исходное значение, умноженную на 100%. Формула выглядит следующим образом:
Процентное приращение = (новое значение – старое значение) / старое значение * 100%
Например, если старое значение равно 100, а новое значение равно 120, процентное приращение будет:
Процентное приращение = (120 – 100) / 100 * 100% = 20%.
Если новое значение меньше старого, например, старое значение равно 120, а новое значение равно 100, процентное приращение будет отрицательным и указывает на уменьшение значения:
Процентное приращение = (100 – 120) / 120 * 100% = -16.67%
Еще один способ расчета процентного приращения – через процент фактического изменения. Формула для этого метода выглядит так:
Процент фактического изменения = (новое значение – старое значение) / старое значение * 100%.
Разница между первым и вторым способом состоит в том, что процент фактического изменения не домножается на 100%. Он показывает величину изменения без учета масштаба.
Например, если старое значение равно 100, а новое значение равно 120, процент фактического изменения будет:
Процент фактического изменения = (120 – 100) / 100 = 0.2 = 20%
Важно учитывать, что проценты предоставляют информацию о доле или доли изменения, и их использование является неотъемлемой частью решения многих задач в финансах, экономике и других областях.
Как решать задачи на процентные приращения?
Решение задач на процентные приращения основывается на простой формуле:
Приращение = Исходное значение * (Процент / 100)
Чтобы применить эту формулу, нужно знать два значения: исходное значение и процент. Исходное значение - это то значение, от которого будем считать процентное приращение. Процент - это число, которое показывает, сколько процентов нужно прибавить или отнять от исходного значения.
В зависимости от задачи, мы можем знать разные значения: начальное значение, конечное значение или само процентное приращение. Но с помощью этой формулы мы всегда сможем определить любое из них.
Например, если нам известно исходное значение и процентное приращение, чтобы найти приращение, нужно умножить исходное значение на процент и разделить на 100. Таким образом, мы получим приращение в виде числа.
Также, зная исходное значение и процентное приращение, мы можем найти конечное значение. Для этого нужно прибавить к исходному значению найденное приращение.
Если у нас есть исходное значение и конечное значение, мы можем найти процентное приращение. Для этого нужно вычесть из конечного значения исходное значение, разделить результат на исходное значение, а затем умножить на 100.
Таким образом, решая задачи на процентные приращения, мы можем находить исходное значение, конечное значение или процентное приращение, в зависимости от того, какие значения у нас есть.
Важно помнить, что знак процента (+ или -) определяет, что нужно делать с исходным значением: прибавить или отнять процентное приращение. Поэтому всегда внимательно читайте условия задач и определяйте, какое действие нужно выполнить.



