Предел функции в точке - одно из основных понятий математического анализа, которое помогает определить поведение функции вблизи определенной точки. Предел позволяет понять, как значения функции приближаются к определенному числу в условиях, когда нельзя просто подставить это число в функцию.
Предел функции в точке можно определить следующим образом: пусть у нас есть функция f(x) и точка a на числовой прямой. Если для любого положительного числа ε мы можем найти такое положительное число δ, что для всех x из промежутка (a - δ, a + δ), отличных от числа a, значения функции f(x) будут находиться в промежутке (L - ε, L + ε), где L - число, то говорят, что предел функции f(x) в точке a равен числу L.
Важно отметить, что предел функции в точке может быть равен числу, плюс бесконечность или минус бесконечность. В таком случае говорят о сходимости или расходимости функции в данной точке.
Предел функции в точке: определение и основные понятия
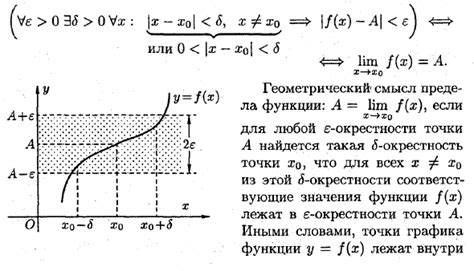
Предел функции в точке определяется так: пусть у нас есть функция f(x), определенная на некоторой окрестности точки a. Говорят, что предел функции f(x) при x стремится к a равен L, если для любого положительного числа ε существует такое положительное число δ, что если x находится в окрестности точки a и отличается от a меньше, чем на δ, то значение функции f(x) будет отличаться от L меньше, чем на ε.
Другими словами, предел функции в точке можно определить как значение, к которому стремится функция при приближении аргумента к данной точке. Если предел существует и равен L, то говорят, что функция f(x) имеет предел при x стремящемся к a и этот предел равен L.
Основные понятия, связанные с пределом функции в точке:
- Окрестность точки - это интервал вокруг данной точки, который содержит все значения, близкие к этой точке. Окрестность часто обозначается как V(a, ε), где a - точка, а ε - положительное число, определяющее ширину окрестности.
- Предел слева - это значение, к которому стремится функция при приближении аргумента к данной точке слева (т.е. значения аргумента меньше a).
- Предел справа - это значение, к которому стремится функция при приближении аргумента к данной точке справа (т.е. значения аргумента больше a).
- Расширенный предел - это значение, к которому стремится функция при приближении аргумента к данной точке, включая случаи, когда аргумент стремится к бесконечности.
- Асимптота - это линия, которая приближает значения функции при приближении аргумента к определенной точке или бесконечности. Асимптота может быть горизонтальной, вертикальной или наклонной, в зависимости от характеристик функции.
Предел функции в точке является важным инструментом для анализа свойств функции и ее поведения вблизи отдельных точек. Он широко используется в математике, физике, экономике и других науках для решения различных задач и моделирования процессов.
Определение предела функции в точке

Формально, говорят, что число L является пределом функции f(x) при x, стремящемся к a, если для любого положительного числа ε найдется такое положительное число δ, что для всех значений аргумента x, отличных от a и удовлетворяющих неравенству |x - a| f(x) - L|
Другими словами, предел функции в точке a равен L, если значения функции f(x) могут быть сколь угодно близкими к L при достаточно близких значениях x и a.
Границы и окрестности точки

При изучении пределов функций в точке важное значение имеют понятия границы и окрестности точки. Рассмотрим их подробнее.
Граница точки
Границей точки \(x_0\) на прямой называется число \(a\), такое что для любого положительного числа \(\epsilon\) найдется точка \(x\), принадлежащая интервалу \((x_0-\epsilon, x_0+\epsilon)\), и при этом \(x
eq x_0\), \(x
eq a\). То есть, в любой проколотой окрестности точки \(x_0\) найдется точка из интервала \((x_0-\epsilon, x_0+\epsilon)\), отличная от самой точки \(x_0\) и границы \(a\).
Окрестность точки
Окрестностью точки \(x_0\) на прямой называется любой интервал \((x_0-\epsilon, x_0+\epsilon)\), где \(\epsilon\) - положительное число. То есть, окрестностью точки является интервал открывающийся слева и справа от точки \(x_0\) и включающий точки, лежащие близко к \(x_0\).
Знание определений границы и окрестности точки необходимо для понимания понятия предела функции в точке, так как предел функции в точке определяется с использованием окрестностей и границ. Понимание границ и окрестностей позволяет более точно описывать поведение функции вблизи определенных точек и проводить дальнейшие исследования функции.
Бесконечно малые и бесконечно большие пределы

Предел функции в точке определение помогает определить поведение функции вблизи данной точки. В некоторых случаях, функция может стремиться к определенному значению, бесконечно малому или бесконечно большому. Эти особенности пределов функций играют важную роль в математическом анализе и при решении различных задач.
Предел функции $f(x)$ называется бесконечно малым в точке $x_0$ если для любого положительного числа $\varepsilon > 0$ существует такое число $\delta > 0$, что для всех $x$, удовлетворяющих неравенству $0
Если предел функции равен нулю при $x$ стремящемся к $x_0$, то $\lim_{x
ightarrow x_0} f(x) = 0$. Функция в этом случае будет иметь график, который всё ближе и ближе подходит к оси $y=0$ при приближении $x$ к $x_0$.
Бесконечно большой предел функции имеет место, когда значение функции становится бесконечно большим при приближении аргумента к указанной точке. Функцию можно назвать бесконечно большой в точке $x_0$, если для каждого положительного числа $M > 0$, существует такое число $\delta > 0$, что для каждого значения $x$, удовлетворяющего условию $0 M$.
Таким образом, бесконечно большой предел функции в точке $x_0$ можно записать как $\lim_{x
ightarrow x_0} f(x) = \infty$. График функции будет описывать асимптоту бесконечности, когда $x$ будет стремиться к $x_0$.
Бесконечно малые и бесконечно большие пределы функций позволяют установить особенности поведения функции вблизи определенных точек, что важно при анализе и решении задач в математике и других науках, где требуется изучение изменений величин и их взаимосвязей.
| Свойство пределов функций | Бесконечно малый предел | Бесконечно большой предел |
|---|---|---|
| Арифметические свойства | Если $f(x)$ и $g(x)$ имеют бесконечно малые пределы в точке $x_0$, то их сумма, разность, произведение и частное также будут иметь бесконечно малый предел. | Если $f(x)$ и $g(x)$ имеют бесконечно большие пределы в точке $x_0$, то их сумма, разность, произведение и частное также будут иметь бесконечно большие пределы. |
| Переход к пределу в неравенстве | Если $f(x)$ имеет бесконечно малый предел в точке $x_0$ и $f(x) \geq g(x)$ при всех значениях $x eq x_0$, то $g(x)$ также будет иметь бесконечно малый предел в этой точке. | Если $f(x)$ имеет бесконечно большой предел в точке $x_0$ и $f(x) \geq g(x)$ при всех значениях $x eq x_0$, то $g(x)$ также будет иметь бесконечно большой предел в этой точке. |
Односторонние пределы функции

Существуют два вида односторонних пределов: левосторонний предел и правосторонний предел. Левосторонний предел функции f(x) в точке c обозначается как f(x) при x стремящемся к c с левой стороны и записывается так: f(x) → L при x → c–. Правосторонний предел функции f(x) в точке c обозначается как f(x) при x стремящемся к c с правой стороны и записывается так: f(x) → L при x → c+.
Если левосторонний и правосторонний пределы существуют и совпадают, то значение этого предела называется двусторонним пределом функции f(x) в точке c и обозначается как f(x) → L при x → c. Двусторонний предел существует только в том случае, когда левосторонний и правосторонний пределы существуют и равны друг другу.
Односторонние пределы функции позволяют определить поведение функции в окрестности точки, когда x стремится к этой точке.
Например, пусть задана функция f(x) = x^2 при x ≤ 2 и f(x) = 2x при x > 2. Чтобы найти левосторонний предел функции в точке x = 2, нужно найти предел функции f(x) = x^2 при x стремящемся к 2 с левой стороны. В данном случае это будет предел функции f(x) = x^2 при x стремящемся к 2 с x ≤ 2. Если мы подставим значения x, близкие к 2 с левой стороны (например, 1.9, 1.99, 1.999 и т.д.), то получим значения функции, которые будут стремиться к 4, значит левосторонний предел функции в точке x = 2 равен 4.
Арифметические свойства пределов

Арифметические свойства пределов функций предоставляют возможность упрощать вычисление пределов при выполнении арифметических операций.
Свойства пределов функций:
- Сумма пределов: Если пределы функций f(x) и g(x) существуют при x → a, то предел их суммы равен сумме пределов: .
- Разность пределов: Если пределы функций f(x) и g(x) существуют при x → a, то предел их разности равен разности пределов: .
- Произведение пределов: Если пределы функций f(x) и g(x) существуют при x → a, то предел их произведения равен произведению пределов: .
- Частное пределов: Если пределы функций f(x) и g(x), причем g(x) ≠ 0, существуют при x → a, то предел их частного равен частному пределов: .
Эти свойства позволяют упростить вычисление пределов функций, а также обобщить их на случай последовательностей, рядов и т.д.
Теоремы о пределах функций

В теории пределов функций существуют различные теоремы, которые позволяют упростить или вычислить пределы функций в различных случаях. Наиболее известные из них:
Теорема о пределе суммы: Если существуют пределы функций f(x) и g(x) при x стремящемся к a, то предел их суммы равен сумме их пределов.
Теорема о пределе произведения: Если существуют пределы функций f(x) и g(x) при x стремящемся к a, то предел их произведения равен произведению их пределов.
Теорема о пределе частного: Если существуют пределы функций f(x) и g(x) при x стремящемся к a, и предел g(x) не равен нулю, то предел их частного равен частному их пределов.
Теорема о пределе составной функции: Если существует предел функции g(x) при x стремящемся к a и существует предел функции f(u) при u стремящемся к b (где b - предел g(x) при x стремящемся к a), то предел составной функции f(g(x)) при x стремящемся к a равен пределу функции f(u) при u стремящемся к b.
Теорема о пределе монотонной функции: Если существует предел монотонной функции f(x) при x стремящемся к a, и значение f(x) ограничено на промежутке (a, b), то предел f(x) при x стремящемся к a равен наибольшему (наименьшему) значению этой функции на промежутке (a, b).
Эти и множество других теорем обеспечивают удобное и эффективное вычисление пределов функций в различных условиях.
Примеры вычисления пределов функций

Вычисление пределов функций позволяет определить поведение функции вблизи заданной точки. Рассмотрим несколько примеров:
- Найдем предел функции f(x) = 2x + 3 при x стремящемся к 5. Для этого подставим x = 5 в функцию и получим значение предела равным 13.
- Рассмотрим функцию g(x) = 1/x. Найдем ее предел при x стремящемся к 0. Подставим x = 0 и получим, что предел функции равен бесконечности.
- Пусть дана функция h(x) = sin(x)/x. Найдем ее предел при x стремящемся к 0. Подставим x = 0 и получим значение предела, равное 1.
Таким образом, вычисление пределов функций позволяет определить их поведение и свойства вблизи конкретных точек. Это является важным инструментом в математике и науке в целом.



