Средняя является одним из наиболее распространенных и важных показателей в статистике. Она используется для измерения и оценки центральной тенденции в наборе данных. Среднее значение представляет собой сумму всех значений, разделенную на их количество.
Средняя обладает свойством репрезентативности: она дает общую характеристику данных, учитывая все имеющиеся значения. Благодаря этому показателю, мы можем легко сравнивать различные наборы данных и выявлять общие тенденции.
Однако, следует помнить, что среднее значение может быть искажено выбросами. Если в наборе данных есть необычно большие или маленькие значения, они могут сильно повлиять на среднее. Поэтому, помимо среднего, часто используют и другие меры центральной тенденции, такие как медиана и мода, чтобы получить более полное представление о данных.
Роль среднего значения
Среднее значение помогает:
- Определить типичное или среднестатистическое значение в выборке или совокупности данных;
- Сравнить результаты между собой;
- Выявить тренды или изменения в данных;
- Прогнозировать будущие значения на основе имеющихся данных.
Среднее значение также может быть использовано для дальнейшего статистического анализа, такого как вычисление дисперсии, стандартного отклонения и других показателей разброса данных.
Однако следует помнить, что среднее значение может быть искажено выбросами или нестандартными значениями в выборке. Поэтому при анализе данных всегда рекомендуется учитывать и другие показатели, такие как медиана или мода.
В целом, среднее значение является мощным инструментом измерения и анализа данных, который может помочь в понимании и описании наблюдений или измерений в статистике.
Виды средних в статистике

В статистике существует несколько типов средних, которые используются для описания и анализа данных. Каждый вид среднего имеет свои особенности и применяется в зависимости от задачи и характеристик исследуемых данных.
1. Арифметическое среднее
Арифметическое среднее является наиболее распространенным и простым видом среднего. Оно рассчитывается путем суммирования всех значений в выборке и деления полученной суммы на количество значений. Арифметическое среднее часто используется для получения общего представления о центральной тенденции данных.
2. Медиана
Медиана представляет собой значение, которое разделяет упорядоченную выборку на две равные части. Для нахождения медианы необходимо упорядочить все значения в выборке по возрастанию и найти значение, стоящее в середине. Если количество значений нечетное, медиана будет равна значению по середине. Если количество значений четное, медиана будет равна среднему арифметическому двух значений, стоящих посередине.
3. Геометрическое среднее
Геометрическое среднее рассчитывается путем умножения всех значений в выборке и извлечения из полученного произведения корня, равному количеству значений. Геометрическое среднее часто используется для нахождения среднего значения величин с логарифмическим распределением.
4. Взвешенное среднее
Взвешенное среднее представляет собой среднее значение, в котором значения в выборке взвешиваются их относительной важностью или весом. Каждому значению присваивается определенный коэффициент веса, и среднее значение рассчитывается путем умножения каждого значения на его вес и деления полученной суммы на сумму всех весов.
5. Среднее гармоническое
Среднее гармоническое рассчитывается путем деления количества значений на сумму обратных величин каждого значения. Среднее гармоническое часто используется для нахождения среднего значения величин с обратно пропорциональным распределением, например, скорости и времени.
Выбор конкретного вида среднего зависит от цели исследования и особенностей данных, поэтому важно выбирать подходящий вид среднего в каждой конкретной ситуации.
Вычисление среднего значения

Для наглядности можно представить вычисление среднего значения в виде таблицы:
| Выборка | Значение |
| 1 | 10 |
| 2 | 15 |
| 3 | 20 |
| 4 | 25 |
Чтобы вычислить среднее значение для выборки, необходимо сложить все значения (10 + 15 + 20 + 25) и разделить их на количество элементов (4).
Среднее значение для данной выборки будет равно 17,5.
Среднее гармоническое

Для вычисления среднего гармонического необходимо первоначально найти единицы, обратные значениям, над которыми будет производиться расчет. Затем, найдя обратные значения каждого из показателей, найдите среднее арифметическое для них. В конечном итоге, вычислите обратное значение среднего арифметического, получив искомое среднее гармоническое.
Среднее гармоническое имеет некоторые особенности, которые следует учитывать при его использовании. Одна из основных особенностей - чувствительность к выбросам. Наличие значений, которые сильно отличаются от остальных, может существенно повлиять на результат расчета среднего гармонического. Поэтому, перед использованием этого метода, важно провести анализ данных и проверить выбросы, чтобы избежать искажения результатов.
Среднее гармоническое является эффективным и надежным инструментом для расчета среднего значения в статистике. Оно широко применяется в различных областях, таких как финансы, экономика, физика и т.д. Важно понимать принципы его расчета и учитывать особенности при его использовании, чтобы получить достоверные и точные результаты.
Среднее арифметическое

Для вычисления среднего арифметического необходимо сложить все значения и разделить полученную сумму на количество значений. Формула для вычисления среднего арифметического выглядит следующим образом:
Среднее арифметическое = (Значение1 + Значение2 + ... + ЗначениеN) / N
Среднее арифметическое является одним из самых простых и распространенных показателей, используемых в статистике. Оно широко применяется в различных областях, включая науку, экономику, социологию и другие.
Среднее геометрическое

Среднее геометрическое вычисляется путем умножения всех значений выборки, а затем извлечения из полученного произведения корня степени, равной количеству этих значений.
Этот вид среднего часто используется для описания средних величин, которые имеют геометрическую природу или распределение.
Среднее геометрическое подчеркивает важность учета всех значений выборки, поскольку оно учитывает их взаимосвязь и взвешенно учитывает их значение при вычислении.
Кроме того, среднее геометрическое часто используется в финансовых расчетах и в других областях, где имеет значение произведение приведенных величин.
Пример:
Допустим, у нас есть выборка с числами 2, 4 и 8. Чтобы вычислить среднее геометрическое, мы умножаем все числа: 2 * 4 * 8 = 64, а затем извлекаем корень кубической степени из этого произведения: ∛64 = 4. Таким образом, среднее геометрическое для данной выборки равно 4.
Среднее геометрическое часто используется совместно с другими мерами статистической центральности, такими как среднее арифметическое и среднее гармоническое, для получения более полного описания распределения значений.
Отличия среднего арифметического от среднего гармонического
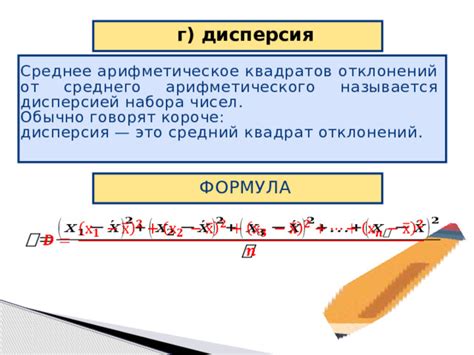
Среднее арифметическое - это наиболее распространенный и простой способ определения среднего значения. Оно рассчитывается путем сложения всех значений и деления полученной суммы на количество значений. Формула для вычисления среднего арифметического выглядит следующим образом:
среднее арифметическое = сумма всех значений / количество значений
Среднее арифметическое является аддитивным показателем, что означает, что оно отражает среднюю "среднюю" величину, позволяя учесть все значения. Это делает его особенно полезным, когда важно учитывать каждое значение, например, при анализе средних ежедневных температур или доходов населения.
Среднее гармоническое, с другой стороны, используется для расчета среднего значения величин, которые обратно пропорциональны. Оно рассчитывается путем деления количества значений на сумму инверсий значений (1/значение), а затем полученный результат инвертируется (1/среднее гармоническое). Формула для вычисления среднего гармонического выглядит следующим образом:
среднее гармоническое = количество значений / (1/значение1 + 1/значение2 + ... + 1/значениеn)
Среднее гармоническое представляет собой гармоническое среднее (среднее обратных величин) и часто используется при измерении величин, таких как скорость, коэффициенты и производительность. Оно особенно полезно, когда необходимо учесть обратную пропорциональность величин и помимо средних значений также важно учитывать экстремально низкие значения.
Таким образом, отличия между средним арифметическим и средним гармоническим заключаются в способе рассчета и применения. Среднее арифметическое является более общим показателем, подходящим для большинства случаев, в то время как среднее гармоническое используется для специфических задач, где обратная пропорциональность играет важную роль.
Применение среднего значения в статистике

Среднее значение играет важную роль в различных областях статистики. Например, в экономике оно позволяет определить средний уровень доходов населения или средние расходы предприятий. В медицине среднее значение используется для определения среднего уровня заболеваемости или эффективности лечения. В образовании оно помогает сравнивать успеваемость студентов или эффективность преподавательского состава.
Кроме того, среднее значение может быть использовано для проверки статистических гипотез. Например, если среднее значение двух выборок существенно различается, это может указывать на наличие статистически значимых различий между этими выборками.
Однако, при использовании среднего значения необходимо учитывать его ограничения. В некоторых случаях оно может быть искажено выбросами или несимметричным распределением данных. Поэтому, наряду со средним значением, обычно используются другие меры центральной тенденции, такие как медиана или мода.
Проблемы использования среднего значения

Проблема выбросов: Среднее значение подвержено влиянию выбросов в данных. Даже одно некорректное наблюдение может значительно искажать результат. Например, если в выборке представлены доходы большинства людей, а также доход миллиардера, среднее значение будет кажется искаженным и не отображать общую картину.
Нерепрезентативность выборки: Если выборка не репрезентативна и не представляет всю генеральную совокупность, среднее значение в выборке может быть неверным. Например, если провести опрос среди студентов и спросить их о доходах, среднее значение будет низким, но это не отражает реальную ситуацию в обществе.
Асимметричность распределения: В распределении данных может присутствовать асимметрия, то есть, среднее значение будет сильно смещено к одному из концов распределения. В этом случае, среднее значение может давать искаженную картину о данных, особенно если интересующая нас величина имеет нормальное распределение.
Проблема отсутствующих данных: Если в выборке есть отсутствующие данные, то использование среднего значения может быть проблематично. Замена отсутствующих значений на среднее может привести к искажению результатов. В такой ситуации, более подходящими могут быть медиана или мода.
Итак, несмотря на все проблемы, среднее значение все же является полезной и информативной мерой центральной тенденции. Однако, при его использовании необходимо помнить о его ограничениях и учитывать другие меры статистики, чтобы получить более полное представление о данных.



