Геометрия – это раздел математики, изучающий фигуры, их свойства и пространственные отношения. В 8 классе обучение этому предмету становится более глубоким и интересным, расширяя представление о геометрии и её применении в реальной жизни.
На уроках геометрии 8 класса ученики познакомятся с новыми фигурами, такими как производные от прямоугольника – параллелограммы, их свойствами и классификацией. Они узнают о площадях различных фигур и научатся решать задачи на нахождение площадей треугольников, параллелограммов и трапеций.
Также в программе 8 класса по геометрии важное место занимают уравнения и неравенства на основе геометрических фигур. Ученики будут изучать геометрические задачи на нахождение неизвестной величины, используя свойства площадей, периметров и отношений сторон фигур. Это развивает их логическое мышление, абстрактное мышление и умение решать сложные задачи.
Основные понятия геометрии

1. Точка - это элемент геометрической фигуры без размеров. В математике обозначается заглавной буквой.
2. Прямая - это множество точек, расположенных по одну сторону от другой. Прямая не имеет начала и конца.
3. Отрезок - это участок прямой, ограниченный двумя точками. Отрезок имеет начало и конец.
4. Луч - это участок прямой, который имеет начало и простирается бесконечно в одном направлении.
5. Угол - это область плоскости, образованная двумя лучами с общим началом, называемым вершиной угла.
6. Параллельные линии - это линии, которые никогда не пересекаются и находятся на одной плоскости.
7. Перпендикулярные линии - это линии, которые пересекаются под прямым углом.
8. Полный угол - это угол, равный 360 градусов или 2π радианов.
Освоение этих основных понятий геометрии поможет в дальнейшем изучении сложных тем и задач в этом разделе математики.
Фигуры и их свойства
В геометрии 8 класса изучаются различные геометрические фигуры и их свойства. Фигуры можно классифицировать по различным признакам, таким как количество сторон, углов или особенности формы.
Прямоугольник - это фигура, у которой все углы прямые (равны 90 градусам) и противоположные стороны параллельны и равны друг другу. Прямоугольник имеет 4 стороны и 4 угла.
Квадрат - это особый вид прямоугольника, у которого все стороны равны друг другу. Квадрат также имеет 4 угла прямые.
Треугольник - это фигура, у которой три стороны и три угла. Углы в треугольнике могут быть различной величины, в зависимости от длин сторон.
Равнобедренный треугольник - это треугольник, у которого две стороны равны друг другу. В таком треугольнике углы при основании равны между собой.
Равносторонний треугольник - это треугольник, у которого все стороны равны друг другу. В таком треугольнике все углы равны 60 градусам.
Круг - это фигура, у которой все точки находятся на одинаковом расстоянии от центра. Круг не имеет сторон и углов, но имеет радиус и диаметр.
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны друг другу.
Трапеция - это четырехугольник, у которого две противоположные стороны параллельны. У трапеции есть одна пара параллельных сторон, называемая основанием, и две другие стороны, называемые боковыми сторонами.
| Фигура | Свойства |
|---|---|
| Прямоугольник | 4 стороны 4 угла прямые |
| Квадрат | 4 стороны равны 4 угла прямые |
| Треугольник | 3 стороны 3 угла |
| Равнобедренный треугольник | 2 стороны равны углы при основании равны |
| Равносторонний треугольник | 3 стороны равны все углы равны 60 градусам |
| Круг | не имеет сторон и углов имеет радиус и диаметр |
| Параллелограмм | противоположные стороны параллельны и равны |
| Трапеция | две противоположные стороны параллельны |
Построение геометрических фигур
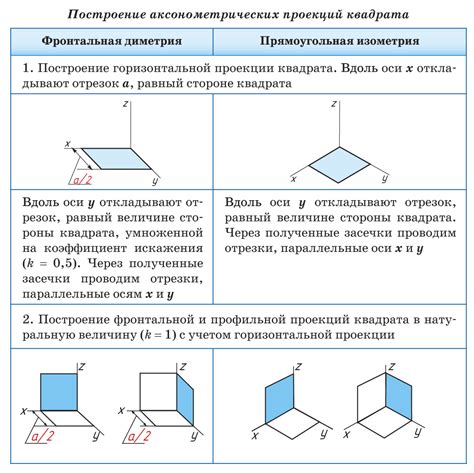
Одним из самых простых способов построения фигур является использование линейки и циркуля. С их помощью можно легко построить отрезки, углы, треугольники, прямоугольники и другие фигуры.
Для построения отрезка необходимо провести два точечных маркера на линейке и соединить их прямой линией. Для построения угла необходимо провести три точечных маркера на линейке и с помощью циркуля провести дугу из одной точки в другую. Затем, соединив концы дуги прямой линией, можно получить нужный угол.
Построение треугольника может быть основано на различных условиях, например, заданной длине сторон или равенстве углов. Для построения треугольников с заданными длинами сторон можно использовать линейку и циркуль. Необходимо отметить на линейке точки, соответствующие длинам сторон, и с помощью циркуля провести дуги, соединив концы дуг прямыми линиями можно построить треугольник.
Построение прямоугольников также может быть выполнено с использованием линейки и циркуля. Для этого необходимо построить две перпендикулярные прямые, а затем провести на них отрезки, имеющие одинаковую длину. Соединив концы отрезков прямыми линиями можно получить прямоугольник.
Кроме того, в геометрии 8 класса изучаются и построения, основанные на специальных построениях, например, построение ортоцентра, центра вписанной окружности и других. Для выполнения таких построений необходимо знать определенные правила и алгоритмы, которые будет изучать в классе.
Важно уметь точно и аккуратно проводить отрезки и линии, использовать инструменты - линейку и циркуль правильно. Это позволит достичь точности и качества в построении геометрических фигур.
Связь между фигурами

Геометрия предлагает нам широкий спектр фигур, и между ними существуют различные связи и взаимосвязи.
Одной из важных концепций в геометрии 8 класса являются подобные фигуры. Две фигуры называются подобными, если у них соответственные углы равны, а соответствующие стороны пропорциональны. Подобные фигуры описывают различные пропорции и отношения между сторонами и углами.
Существуют также фигуры, которые являются частными случаями друг друга. Например, прямоугольник является частным случаем параллелограмма, треугольник является частным случаем четырехугольника. Эти связи между фигурами помогают нам лучше понять и классифицировать геометрические объекты.
Еще одним важным понятием в геометрии 8 класса является геометрическое место точек. Геометрическое место точек - это множество точек, которые удовлетворяют определенному условию. Например, окружность - это геометрическое место точек, которые находятся на одинаковом расстоянии от центра окружности. Геометрические места точек помогают нам строить и анализировать различные геометрические фигуры и применять их в практических задачах.
Чтобы успешно изучать геометрию восьмого класса, важно понимать связь между различными фигурами и уметь анализировать их особенности и свойства. Знание этих связей поможет вам лучше понять геометрические теоремы и использовать их в решении задач.
Поэтому, изучение связей между фигурами является фундаментальным элементом изучения геометрии восьмого класса.
Способы измерения фигур

Измерение фигур в геометрии играет важную роль, так как позволяет определить их характеристики и свойства. Существует несколько способов измерения различных фигур, которые мы широко используем в 8 классе.
Одним из способов измерения фигур является их периметр. Периметр фигуры - это сумма длин всех ее сторон. Например, чтобы измерить периметр прямоугольника, нужно просуммировать длины всех его сторон: P = 2a + 2b, где a и b - длины сторон прямоугольника.
Другим способом измерения фигур является их площадь. Площадь фигуры - это количество площадных единиц, которые помещаются внутри нее. Например, чтобы измерить площадь прямоугольника, нужно умножить длину одной из его сторон на длину другой стороны: S = a * b, где a и b - длины сторон прямоугольника.
Радиус круга - это другая характеристика фигуры, которую необходимо измерить. Радиус (r) - это расстояние от центра круга до любой его точки. Измерение радиуса позволяет определять площадь и длину окружности круга: S = πr^2 и C = 2πr, где π - математическая константа, примерное значение которой равно 3.14.
Таким образом, измерение фигур в геометрии позволяет определить их характеристики и свойства, а также применять эти знания на практике при решении задач и построении графиков.
Теоремы о прямых и углах
1. Угол в полуокружности: если вершина угла и начало и конец дуги, по которой они ограничены, лежат на одной окружности, то угол между этими дугами равен половине прямого угла.
2. Внешний угол треугольника: внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
3. Теорема сторон угла: если известны две прямые, образующие угол, и стороны этого угла пересекаются с третьей прямой, то сумма отрезков задаёт длину этой третьей прямой.
Примечание: эти теоремы могут использоваться для доказательства других утверждений и решения задач на построение и измерение углов. Важно уметь применять их в различных геометрических ситуациях.
Разделяющие теоремы и формулы
Перпендикулярные прямые:
Между двумя перпендикулярными прямыми существует особое взаимоотношение - они создают углы, равные 90 градусам. Это свойство можно использовать для решения различных геометрических задач.
Угол-биссектриса:
Угол-биссектрисой называется прямая, которая делит угол на два равных угла. Знание угла-биссектрисы позволяет определить равные углы и решить такие задачи как построение углов, нахождение отношения между сторонами треугольника и многое другое.
Формулы для площади и периметра:
Площадь и периметр являются основными характеристиками геометрических фигур. Для различных фигур существуют специальные формулы, позволяющие вычислять их площадь и периметр. Некоторые из них:
- Для прямоугольника: S = a * b, P = 2a + 2b, где a и b - длины сторон прямоугольника.
- Для квадрата: S = a^2, P = 4a, где a - длина стороны квадрата.
- Для треугольника: S = (1/2) * a * h, P = a + b + c, где a, b и c - длины сторон треугольника, h - высота, опущенная на основание.
Теорема Пифагора:
Одна из наиболее известных теорем в геометрии - теорема Пифагора. Она устанавливает связь между длинами сторон прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов. Эта теорема широко применяется при решении задач на вычисление длины сторон треугольника.
Теоремы о треугольниках
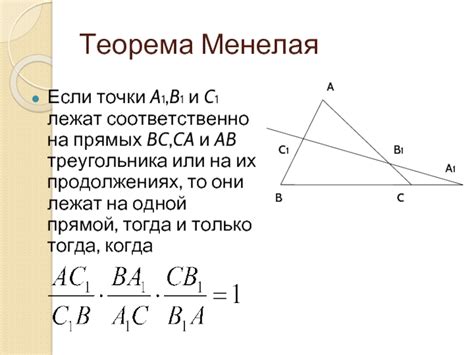
Геометрия треугольников основывается на множестве теорем и правил, которые позволяют нам анализировать и изучать свойства треугольников. В данном разделе мы рассмотрим несколько основных теорем о треугольниках.
Теорема о сумме углов треугольника: В остроугольном треугольнике сумма его углов равна 180 градусам. В прямоугольном треугольнике сумма его прямых углов также равна 180 градусам.
Теорема о равенстве треугольников: Если у двух треугольников все стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника, то эти треугольники равны.
Теорема о прямоугольном треугольнике: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это называется теоремой Пифагора.
Теорема о пропорциональности сторон треугольников: Если два треугольника подобны, то отношение любой стороны одного треугольника к соответствующей стороне другого треугольника равно отношению любой другой стороны первого треугольника к соответствующей стороне второго треугольника.
Теорема о биссектрисе: Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные смежным сторонам треугольника.
Эти теоремы играют важную роль в анализе и построении треугольников. Они помогают нам понять свойства треугольников и решать различные задачи в геометрии.
Площадь и периметр фигур
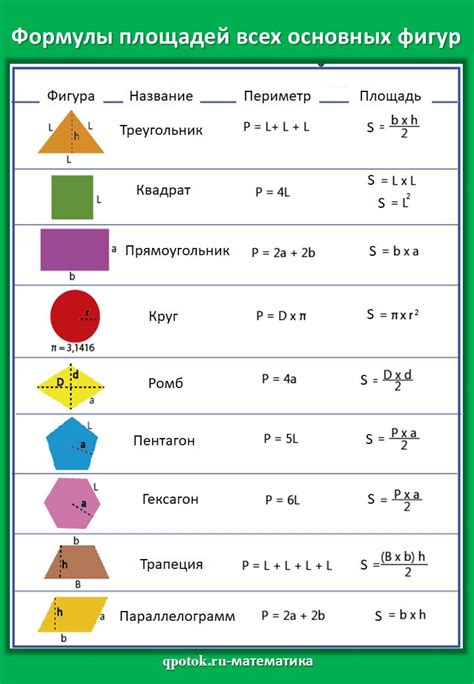
Периметр – это сумма длин всех сторон фигуры. Он измеряется в единицах длины: метрах, сантиметрах и т.д. Периметр позволяет определить длину контура фигуры.
Для разных фигур есть разные формулы для вычисления площади и периметра:
1. Прямоугольник: Периметр – это удвоенная сумма длины и ширины фигуры, а площадь – это произведение длины и ширины.
2. Квадрат: Периметр – это четыре умноженное на длину стороны фигуры, а площадь – это квадрат длины стороны.
3. Круг: Периметр круга называется окружностью, а площадь – это произведение числа пи на квадрат радиуса.
4. Треугольник: Периметр – это сумма длин трех сторон фигуры, а площадь – это половина произведения длины основания на высоту.
Зная формулы для вычисления площади и периметра, можно легко определить эти величины для любой заданной фигуры. Это инструменты, которые помогают в решении задач и в анализе геометрических фигур.
Решение задач по геометрии

Решение задач по геометрии требует от нас умения анализировать геометрические фигуры, применять свойства и формулы, а также логически мыслить. В этом разделе мы рассмотрим основные шаги решения задач и приведем примеры вычислений.
Шаг 1: Понимание условия
Перед началом решения задачи необходимо внимательно прочитать условие и понять, что от нас требуется. Важно выделить ключевые данные и факты, которые помогут нам в решении задачи.
Шаг 2: Обозначение неизвестных
Для удобства мы обозначаем неизвестные значения, используя переменные или буквы. Это позволяет нам работать с абстрактными значениями и формулами.
Шаг 3: Анализ фигур и применение свойств
На данном этапе мы анализируем геометрические фигуры, выделяем данную информацию и применяем соответствующие свойства и формулы. Знание основных свойств треугольников, прямоугольников, кругов и др. позволяет нам решать задачи более эффективно.
Шаг 4: Построение уравнений
Здесь мы формулируем и записываем необходимые уравнения, используя полученные данные и свойства фигур. Уравнения помогают нам связать разные величины и найти решение задачи.
Шаг 5: Вычисления и ответ
Внимательно решаем уравнения и осуществляем необходимые вычисления. Полученный результат является ответом на поставленную задачу.
Продуктивность в решении задач по геометрии приходит с практикой. Чем больше задач вы решите, тем более легко вам будет применять свойства и формулы, а также видеть скрытые паттерны решения. Не бойтесь экспериментировать и учиться на ошибках, а геометрия станет вашим надежным помощником в решении задач различной сложности.
Практическое применение геометрии

Одним из самых явных применений геометрии является строительство. Без геометрии невозможно построить прочные и устойчивые здания и сооружения. Геометрические принципы применяются при определении формы и размеров строительных элементов, расчете углов и расстояний, а также для создания планов и чертежей.
Геометрия также имеет применение в архитектуре. Архитекторы используют геометрические формы и пропорции для создания красивых и гармоничных зданий. Они также учитывают геометрические принципы при планировании помещений, распределении мебели и организации пространства.
В инженерии геометрия играет важную роль при проектировании и конструировании машин и механизмов. Инженеры используют геометрические принципы для определения формы и размеров деталей, расчета углов и сил, а также для проверки прочности и устойчивости конструкций.
Геометрия также применяется в картографии и навигации. Картографы используют геометрические методы для создания и измерения карт, определения масштаба и расстояний. Навигаторы и пилоты также используют геометрию для определения своего положения, расчета направлений и углов.
Кроме того, геометрия находит применение в различных естественных и научных науках. Она используется для изучения формы и свойств фигур, решения задач оптимизации, моделирования и представления данных. Геометрия также применяется в компьютерной графике, архитектуре процессоров и программировании.
Практическое применение геометрии распространено во многих сферах нашей жизни. Понимание и усвоение геометрических принципов поможет нам лучше понимать окружающий мир, развивать креативное мышление и находить решения для различных задач.



