Понятие касательной линии к графику функции является одним из основных понятий математического анализа. Касательная линия определяет направление и скорость изменения функции в данной точке. Очень часто в учебниках можно найти упражнения, в которых нужно найти уравнения касательных к графикам функций в заданных точках. Однако не всегда на первый взгляд очевидно, что любая хорда графика функции может быть интерпретирована как некая апроксимация касательной к этому графику.
Для доказательства этого факта рассмотрим любую хорду графика функции. Определим точки, через которые проходит эта хорда. Далее проведем касательные к графику функции в этих точках. Внимательно рассмотрев и проведя несложные геометрические рассуждения, мы можем определить, что эти касательные исключительно тесно связаны с исходной хордой. Касательные к графику функции образуют ее некие приближения, которые также являются хордами, но с бесконечно малым отклонением от настоящих касательных.
Итак, любая хорда графика функции может быть рассмотрена как секущая касательная, если рассматривать такую хорду как особый случай касательной, чья длина стремится к нулю. Это свойство позволяет упростить задачу нахождения касательной к графику функции в заданной точке, заменяя ее по сути на решение задачи нахождения уравнения хорды, проходящей через эту точку.
Определение секущей касательной
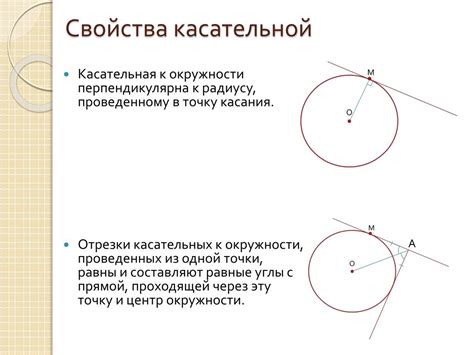
Секущая касательная может быть использована для приближенного определения точек пересечения графика функции с осью абсцисс или другими осевыми линиями.
Для определения секущей касательной необходимо выбрать две точки на графике функции и провести прямую через них. Чем ближе эти точки к точке касания с графиком функции, тем точнее будет приближение касательной линии.
Общий вид графика функции
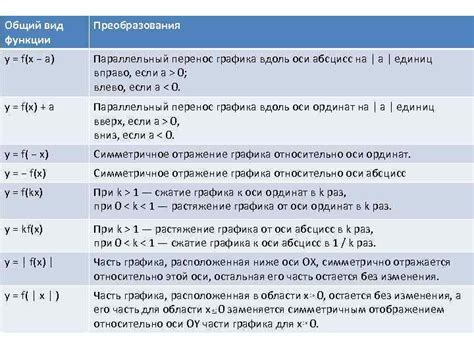
График функции представляет собой визуальное представление зависимости между аргументом и значением функции. Каждая точка на графике соответствует определенному значению функции при данном аргументе.
Для построения графика функции необходимо определить область определения функции, выбрать несколько значений аргумента и вычислить соответствующие значения функции. Затем строится система координат, где горизонтальная ось представляет значения аргумента, а вертикальная ось - значения функции.
На графике функции можно выделить несколько характерных особенностей:
| Особенность | Описание |
|---|---|
| Увеличение/уменьшение функции | Если значения функции с увеличением аргумента также увеличиваются, то график функции будет возрастать. Если значения функции уменьшаются при увеличении аргумента, то график функции будет убывать. |
| Экстремумы | Экстремумы функции - это точки, где функция достигает наибольшего или наименьшего значения. Они обычно выделяются из основного графика функции. |
| Асимптоты | Асимптоты - это прямые или кривые, которым график функции стремится при удалении от начала координат. Они могут быть горизонтальными, вертикальными или наклонными. |
| Периодические функции | Периодическая функция повторяется с некоторым заданным интервалом времени. График периодической функции имеет характерные повторяющиеся фигуры. |
Знание общего вида графика функции позволяет удобно исследовать ее свойства и использовать в различных математических задачах и приложениях.
Хорда графика функции
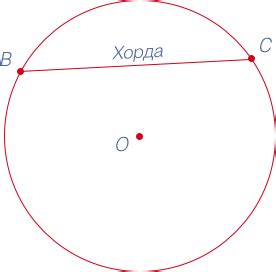
Когда хорда графика функции соединяет две точки, она становится секущей. Секущая - это прямая линия, которая касается графика функции только в двух точках и проходит через другую точку.
Изучение хорды графика функции позволяет нам лучше понять поведение функции. Анализ хорды помогает определить наклон функции между двумя точками, а также может быть использован для вычисления скорости изменения функции в определенном интервале.
Для определения уравнения хорды графика функции необходимо знать координаты двух точек, через которые она проходит. Используя эти координаты, можно найти угловой коэффициент хорды и уравнение прямой, соответствующей данной хорде.
Связь хорды и секущей касательной
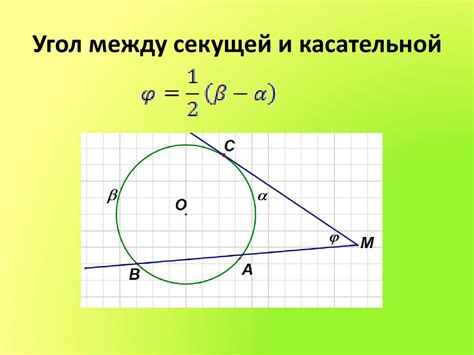
Чтобы понять эту связь, рассмотрим геометрическую интерпретацию производной. Пусть у нас есть функция f(x), и мы хотим построить секущую касательную в точке x=a. Для этого выберем вторую точку на графике функции с координатами x=a+h, где h – малое приращение.
Теперь построим хорду, соединяющую эти две точки. Если h стремится к нулю, то эта хорда будет все ближе и ближе к касателной, а ее наклон будет все больше приближаться к наклону касательной в точке x=a. Таким образом, мы получаем, что хорда, соединяющая две близкие точки на графике функции, является приближением секущей касательной.
Таким образом, можно сказать, что любая хорда графика функции – это приближение секущей касательной. Однако, чтобы получить точную касательную, необходимо производную функции в точке x=a.



