Математика – это неотъемлемая часть нашей жизни. Одним из ее главных инструментов является возведение в степень. Это арифметическая операция, которая позволяет нам умножать число на себя несколько раз и получать результат.
Возведение в степень имеет множество применений в различных областях науки, техники, экономики и даже повседневной жизни. Например, оно используется для расчетов капитализации, прогнозирования роста населения, моделирования физических явлений и многих других задач.
Операция возведения в степень осуществляется путем умножения числа (основания) на себя несколько раз в соответствии со значением показателя (степени). В математической нотации это записывается как a^b, где a – основание, b – показатель степени.
Показатель степени может быть как положительным, так и отрицательным, а также нулевым. В случае положительной степени, число a умножается на себя b раз. В случае отрицательной степени, число a возводится в обратную величину степени |b|. В случае нулевой степени, результатом всегда будет единица, независимо от значения основания.
Что такое степень и почему важно знать о ней?

Знание степень является важным для понимания и решения различных задач в научных и инженерных областях. Оно позволяет обрабатывать большие и сложные числовые данные, применять математические модели и формулы, а также делать точные расчеты и предсказания.
В физике, химии, экономике и других науках степени используются для описания закономерностей и взаимосвязей между различными величинами. Например, в физике для описания движения тела применяются степенные функции, а в экономике для моделирования роста и развития рынка используется экспоненциальная функция.
Кроме того, степени находят широкое применение в информатике и программировании. Они используются, например, для шифрования данных и создания сложных алгоритмов. Знание степени помогает оптимизировать код, ускоряет выполнение программ и повышает эффективность вычислений.
Определение степени и ее математическое значение

Степень состоит из двух составляющих:
- основание - это число, которое возводится в степень;
- показатель - это число, на которое возводится основание.
Математическое обозначение степени выглядит следующим образом:
основаниепоказатель
Например, степень числа 2 возводится в степень 3 выглядит как 23 и равно 2 * 2 * 2 = 8.
Степень имеет много практических применений, например:
- В физике степень используется для вычисления значений величин, подверженных экспоненциальному росту или убыванию.
- В экономике степень используется для расчета процента изменения цен, налоговых ставок и т.д.
- В компьютерных науках степень используется для выполнения сложных вычислений и шифрования данных.
Простая и сложная степень: в чем разница?

Существует два вида степеней: простая и сложная.
Простая степень - это когда число возводится в степень, равную натуральному числу (1, 2, 3 и так далее). Например, 2 возводится в степень 3: 23 = 2 * 2 * 2 = 8.
Сложная степень - это когда число возводится в степень, равную дробному или отрицательному числу. Например, 2 возводится в степень 0.5: 20.5 = √2 ≈ 1.41. Здесь результатом не является целое число, так как мы берем квадратный корень из числа 2.
Таким образом, основная разница между простой и сложной степенью заключается в том, что простая степень дает целочисленный результат, а сложная степень может давать нецелочисленный или даже комплексный результат. Сложные степени широко используются в математических расчетах и в различных областях науки.
Возведение числа в отрицательную степень
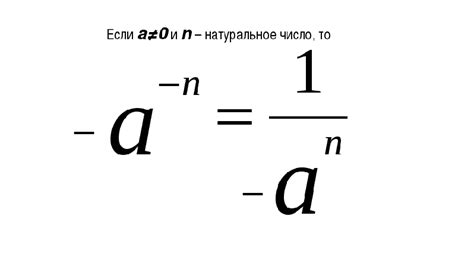
При возведении числа в отрицательную степень, результат будет равен обратному значению числа, возведенного в абсолютную величину данной степени. Например, если числу 2 возвести в степень -3, то результат будет равен 1 / (2^3) = 1 / 8 = 0.125.
Возведение числа в отрицательную степень может быть полезным при решении математических задач, таких как вычисление корней с помощью степени. Например, чтобы найти квадратный корень числа, можно возвести это число в степень 0.5.
Операция возведения числа в отрицательную степень также имеет свои математические свойства. Например, при умножении чисел, возведенных в отрицательные степени, их степени складываются. То есть, если a и b - числа, а их отрицательные степени равны x и y соответственно, то a^-x * b^-y = (a * b)^-(x + y).
Важно помнить, что при возведении числа в отрицательную степень результат может быть дробным или десятичным числом. Также в рамках операции возведения числа в отрицательную степень нужно быть внимательным к возможным ошибкам округления и погрешностям при вычислениях.
Применение степеней в различных областях

- Математика: степени обладают огромной значимостью в математике. Они используются для решения задач, связанных с арифметикой, алгеброй, геометрией и теорией вероятностей.
- Физика: в физике степени применяются для описания законов природы. Например, в законе всемирного тяготения степень используется для определения взаимодействия между двумя телами.
- Инженерия: в инженерии степени используются для моделирования и анализа систем. Они позволяют рассчитать различные параметры и оптимизировать процессы.
- Экономика: в экономике степени применяются для построения экономических моделей, прогнозирования и анализа данных. Они позволяют принимать рациональные решения и оптимизировать деятельность предприятий.
- Компьютерные науки: степени играют важную роль в программировании и алгоритмах. Они используются для выполнения сложных математических вычислений, шифрования данных и создания компьютерных моделей.
- Естественные науки: степени применяются для описания физических и химических явлений. Они помогают объяснить различные природные процессы и явления.
- Медицина: в медицине степени используются для проведения различных исследований и анализа данных. Они помогают определить вероятность возникновения определенных заболеваний или рассчитать необходимую дозу лекарственных препаратов.
Таким образом, применение степеней широко распространено в различных областях и играет важную роль в науке, технике, экономике и других сферах человеческой деятельности.



