Неравенства представляют собой математические выражения, которые говорят о неравенстве значений двух выражений или функций. Они являются основополагающими элементами в алгебре и анализе. Как и в уравнениях, в неравенствах могут происходить изменения знака, что делает их решение более сложным и интересным.
Основными причинами изменения знака в неравенствах являются:
- Умножение или деление на отрицательное число. Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства меняется на противоположный. Например, из неравенства -3x > 6 получаем x < -2.
- Умножение или деление на положительное число. Если обе части неравенства умножить или разделить на положительное число, то знак неравенства остается неизменным. Например, из неравенства 2y < 8 получаем y < 4.
- Прибавление или вычитание положительного числа. Если к обеим частям неравенства прибавить или вычесть положительное число, то знак неравенства остается неизменным. Например, из неравенства x - 5 > 2 получаем x > 7.
- Прибавление или вычитание отрицательного числа. Если к обеим частям неравенства прибавить или вычесть отрицательное число, то знак неравенства меняется на противоположный. Например, из неравенства y + 3 > -4 получаем y > -7.
Понимание причин изменения знака в неравенствах позволяет более точно и эффективно решать задачи, связанные с нахождением интервалов и числовых решений. Также это является важным инструментом при изучении систем неравенств и построении графиков.
Значимость понимания причин изменения знака в неравенствах

Изменение знака в неравенствах возникает при выполнении определенных условий. Эти условия могут быть связаны с операциями, значениями переменных или ограничениями задачи. Когда мы понимаем эти причины, мы можем более точно решать уравнения и неравенства, а также анализировать результаты их решения.
Например, в экономике и финансах понимание причин изменения знака в неравенствах помогает нам анализировать и предсказывать динамику рынка и принимать обоснованные инвестиционные решения. В инженерии и науке это знание позволяет нам решать сложные технические проблемы, оптимизировать процессы и прогнозировать результаты экспериментов.
В образовательной сфере понимание причин изменения знака в неравенствах помогает учащимся развивать критическое мышление, логическое рассуждение и аналитические навыки. Это знание также полезно при подготовке к экзаменам и тестам, где задачи с неравенствами часто встречаются.
Таким образом, понимание причин изменения знака в неравенствах имеет глубокое значение для различных областей знания и позволяет нам применять математические концепции в реальном мире. Оно помогает нам принимать обоснованные решения, решать сложные задачи и развивать критическое мышление. Изучение этой темы является важным этапом в математическом образовании и способствует развитию навыков, необходимых для успешной карьеры в различных сферах.
Фундаментальные принципы математики

1. Принцип эквивалентности
Этот принцип заключается в том, что если две величины или выражения равны одному и тому же числу, то их можно заменить друг на друга в любом математическом соотношении без изменения его верности.
2. Принцип замены
Этот принцип утверждает, что если два выражения равны, то любое из них может быть заменено на другое без изменения истинности равенства.
3. Принцип сохранения порядка
Этот принцип говорит о том, что если два числа сравнимы по величине с третьим числом, то эти два числа сравнимы и между собой.
4. Принцип ассоциативности
Этот принцип утверждает, что порядок, в котором выполняются операции, не влияет на результат. Например, при сложении или умножении нескольких чисел, их порядок может быть изменен, и результат останется неизменным.
5. Принцип дистрибутивности
Этот принцип говорит о том, что произведение или разность двух чисел может быть распределено на несколько сумм или разностей.
Эти фундаментальные принципы математики являются основой для понимания и применения различных математических концепций и методов, включая изменение знака в неравенствах.
Влияние коэффициентов на направление неравенства
Коэффициенты, присутствующие в неравенствах, играют важную роль в определении их направления. Они определяют, будет ли неравенство строгим (строгое неравенство) или независимым (нестрогое неравенство).
Если коэффициент при переменной положительный, то направление неравенства сохраняется. Например, если у нас есть неравенство 2x > 6, то умножение обеих частей на положительное число, такое как 2, сохранит его строгое направление: 4x > 12.
Однако, если коэффициент при переменной отрицательный, направление неравенства меняется. Например, при умножении обеих частей неравенства -3x > 9 на -1, получаем 3x < -9, где строгое неравенство становится обратным.
Таким образом, важно учитывать коэффициенты при переменных при решении неравенств, чтобы правильно определить их направление и получить корректное решение.
Роль отрицательных чисел в изменении знака

Отрицательные числа играют важную роль при изменении знака в неравенствах. Они вносят свою специфику в применение правил сравнения и позволяют учитывать различные ситуации.
Одним из ключевых свойств отрицательных чисел является то, что при умножении на отрицательное число знак неравенства меняется:
- Если положительное число умножить на отрицательное, то знак неравенства изменится на противоположный.
- Если отрицательное число умножить на положительное, то знак неравенства также изменится на противоположный.
Например, пусть дано неравенство 3x > -6. Если умножить обе части неравенства на -1 (отрицательное число), получим: -3x на
Кроме того, отрицательные числа влияют на суммирование чисел с разными знаками:
- При сложении положительного и отрицательного числа, знак результата будет совпадать со знаком числа с большим модулем.
- При сложении двух отрицательных чисел, знак результата также будет отрицательным.
Например, если сложить 5 и -8, получим -3. Здесь отрицательное число -8 имеет больший модуль, поэтому знак суммы будет отрицательным.
Таким образом, использование отрицательных чисел позволяет уточнить правила изменения знака в неравенствах и учесть различные ситуации, что является необходимым в алгебре и математических расчетах.
Взаимосвязь неравенств и промежутков на числовой прямой
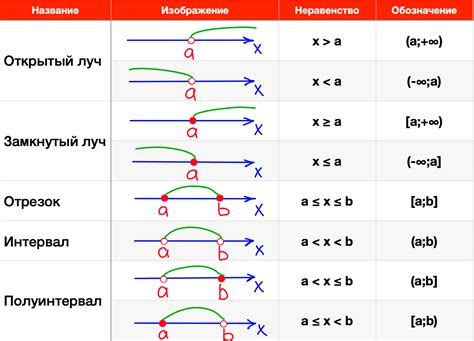
Неравенства играют важную роль в теории чисел и анализе, и их представление на числовой прямой позволяет наглядно исследовать их свойства. У каждого неравенства есть соответствующий промежуток на числовой прямой, и наоборот, каждый промежуток можно представить как неравенство.
Промежутки на числовой прямой можно классифицировать на основе знака неравенства. Если в неравенстве используется знак "=", то промежуток будет закрытым слева. Если же неравенство имеет знак ">", то промежуток будет открытым справа. Аналогично, если знак неравенства ">=" или "
Промежутки на числовой прямой могут быть конечными или бесконечными. Конечные промежутки имеют определенные конечные значения на числовой прямой, в то время как бесконечные промежутки распространяются до бесконечности в одном или обоих направлениях.
Изучение взаимосвязи неравенств и промежутков на числовой прямой помогает понять, как изменятся значения переменной в рамках неравенства. Это незаменимый инструмент для решения уравнений, систем уравнений и задач, связанных с неравенствами.
Вариации алгебраических действий и их воздействие на знаки

При решении неравенств и выполнении алгебраических действий часто возникают ситуации, когда знак в неравенстве меняется в зависимости от выполняемой операции. Основные вариации алгебраических действий, которые влияют на знаки, включают:
1. Сложение и вычитание чисел: при сложении положительного числа к неравенству, знак не меняется, а при вычитании - меняется на обратный.
2. Умножение и деление чисел: при умножении или делении неравенство на положительное число, знак не меняется, однако при умножении или делении на отрицательное число, знак меняется на противоположный.
3. Изменение стороны: перенос одной или нескольких переменных на другую сторону неравенства может привести к изменению знака. Например, если переменная была на левой стороне и перешла на правую, знак неравенства меняется на противоположный.
4. Возведение в степень: при возведении неравенства в нечетную степень, знак остается неизменным. Однако, при возведении в четную степень, необходимо учитывать знак числа, так как отрицательные числа при возведении в четную степень становятся положительными.
При работе с неравенствами и применении алгебраических действий необходимо быть внимательным и тщательно проверять изменения знаков, чтобы избежать ошибок в решении.
Влияние корней и степеней на изменение знака

При решении неравенств с использованием корней и степеней, важно учитывать их влияние на изменение знака.
Корни и степени могут быть представлены как положительными, так и отрицательными числами. В зависимости от знака корня или степени, результат неравенства может изменяться.
1. Корни. Если корень четного порядка (квадратный корень, кубический корень и т. д.) извлекается из положительного числа, то результат всегда будет положительным. Если же корень четного порядка извлекается из отрицательного числа, то результатом будет мнимое число, что не может быть удовлетворено в области действительных чисел.
2. Степени. Если число возводится в нечетную степень, знак числа сохраняется. Так, положительное число, возведенное в нечетную степень, остается положительным, а отрицательное число в нечетной степени остается отрицательным. Однако, если число возводится в четную степень, знак числа меняется на положительный независимо от исходного знака.
Эти особенности корней и степеней могут повлиять на решение неравенств при использовании этих операций. При изменении знака в неравенстве, необходимо учитывать корни и степени и применять соответствующие правила для получения правильного результата.
Интерпретация графического представления неравенств

При интерпретации графического представления неравенства необходимо учитывать следующие аспекты:
- Ось координат: Неравенство может быть представлено на плоскости с помощью графика функции, где ось абсцисс (горизонтальная ось) отражает одну переменную, а ось ординат (вертикальная ось) - другую переменную. Расположение неравенства на графике будет зависеть от числового значения параметров и операторов неравенства.
- Направление стрелки: Знак неравенства определяет направление стрелки на графике. Например, неравенство "x < 5" будет представлено стрелкой, указывающей влево, т.к. оно означает, что значение переменной x находится слева от числа 5.
- Тип стрелки: Если неравенство содержит строгий знак ("<" или ">"), то стрелка будет пустой, что означает, что значение переменной не может равняться числу, указанному в неравенстве. Если неравенство содержит нестрогий знак ("≤" или "≥"), то стрелка будет закрашена, что означает, что значение переменной может равняться числу, указанному в неравенстве.
- Разбиение плоскости: Графическое представление неравенства может включать разбиение плоскости на две или более области в зависимости от числовых значений переменных. Если true значения неравенства находятся внутри области, то false значения - вне области.
Имея графическое представление неравенств, можно производить различные операции с ними, включая объединение и пересечение нескольких неравенств, нахождение области их пересечения и другие. Это позволяет более точно анализировать свойства неравенств и применять их в различных задачах и моделях.
Значимость понимания причин изменения знака для решения прикладных задач

Одной из основных причин изменения знака в неравенствах является введение дополнительных ограничений или условий. В прикладных задачах часто возникают ситуации, когда требуется учесть дополнительные условия, которые могут привести к изменению знака в неравенстве. Например, при решении задачи о площади трапеции, введение условия, что боковые стороны должны быть положительными числами, может привести к изменению знака в неравенстве, если одна из сторон становится отрицательной.
Кроме того, изменение знака в неравенстве может быть обусловлено изменением значений переменных или параметров задачи. В прикладных задачах значения переменных и параметров могут меняться в зависимости от ряда факторов, и изменение этих значений может привести к изменению знака в неравенстве. Например, при решении задачи о доходности инвестиций, изменение процентной ставки может привести к изменению знака в неравенстве, так как является фактором, влияющим на решение задачи.
Также, понимание причин изменения знака в неравенствах позволяет определить допустимые значения переменных или параметров задачи. В прикладных задачах часто требуется определить диапазон значений переменных или параметров, при которых неравенство остается корректным. Знание причин изменения знака в неравенствах позволяет определить эти диапазоны и правильно ограничить значения переменных или параметров задачи.
Таким образом, понимание причин изменения знака в неравенствах является важным элементом при решении прикладных задач. Это позволяет правильно интерпретировать результаты, учитывать дополнительные условия и определить допустимые значения переменных или параметров задачи. При решении прикладных задач необходимо уделять особое внимание этому аспекту и применять соответствующие стратегии для получения точных и корректных результатов.



