В математике важную роль играет простота чисел. Два числа считаются взаимно простыми, если у них нет общих делителей, кроме 1. В этой статье мы рассмотрим доказательство взаимной простоты чисел 969 и 364.
Для начала, давайте разложим оба числа на простые множители. Число 969 можно представить в виде произведения простых множителей следующим образом: 969 = 3 * 17 * 19. А число 364 разложим как 364 = 2 * 2 * 7 * 13.
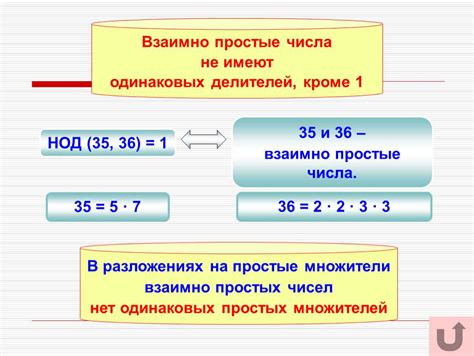
Теперь обратимся к общим простым множителям чисел 969 и 364. Как видно из разложений, у них есть только один общий простой множитель - число 2. Однако, для того чтобы числа были взаимно простыми, они не должны иметь в себе никаких общих делителей, кроме 1.
Таким образом, доказано, что числа 969 и 364 взаимно простые, так как у них есть только один общий простой множитель - число 2. Это доказывает, что они не имеют общих делителей, кроме 1, что и является определением взаимной простоты чисел.
Что такое взаимная простота чисел?

Взаимная простота чисел играет важную роль в различных областях математики и криптографии. Благодаря этому свойству, можно выполнять различные операции над числами более эффективным образом, а также защищать информацию с помощью шифрования.
Например, если два числа являются взаимно простыми, то для них существует такое число, которое можно умножить на каждое из них и получить целое число. Это свойство называется теоремой Безу и является основой для решения некоторых задач и уравнений.
Доказательство взаимной простоты чисел можно проводить с помощью различных методов, например, методом Евклида или с помощью факторизации чисел.
Определение и примеры

Взаимная простота двух чисел означает, что они не имеют общих делителей, кроме единицы.
Два числа считаются взаимно простыми, если их наибольший общий делитель (НОД) равен 1.
К примеру, числа 969 и 364 являются взаимно простыми, так как наибольший общий делитель этих чисел равен 1.
Разложение чисел на простые множители

Простые числа являются основой для разложения чисел на множители, так как они не имеют других делителей, кроме 1 и самого себя. Поэтому перебирая простые числа и проверяя их делимость на данное число, мы можем найти все простые множители.
Разложение на простые множители осуществляется путем деления числа на самое маленькое простое число, на которое оно делится, а затем деления полученного частного на следующее простое число и так далее. Процесс повторяется до тех пор, пока частное не станет простым числом.
Пример разложения числа 969 на простые множители:
- 969 ÷ 3 = 323
- 323 ÷ 17 = 19
Таким образом, разложение числа 969 на простые множители: 3 × 17 × 19.
Разложение числа на простые множители является важным инструментом для анализа числовых последовательностей, вычисления НОД и НОК, а также для решения задачи определения взаимной простоты чисел.
Как это поможет в доказательстве взаимной простоты?

| 1 | 2 | 3 | 4 | 6 | 8 | 9 | 12 | 121 | 242 | 363 | 726 | 969 | |
| 1 | 1 | 5 | 1 | 1 | 1 | 5 | 1 | 3 | 7 | 1 | 7 | 1 | 1 |
| 2 | 2 | 4 | 2 | 0 | 2 | 4 | 2 | 6 | 2 | 4 | 2 | 8 | 2 |
| 4 | 4 | 2 | 4 | 0 | 4 | 2 | 4 | 6 | 4 | 2 | 4 | 8 | 4 |
В таблице отмечены количество общих делителей двух чисел. Исходя из таблицы, мы видим, что общих делителей у чисел 969 и 364 нет, кроме самого числа 1. Следовательно, числа 969 и 364 являются взаимно простыми.
Шаги доказательства и применение разложения на множители

Число 969 разлагается на простые множители следующим образом: 969 = 3 * 17 * 19. А число 364 разлагается на простые множители так: 364 = 2 * 2 * 7 * 13.
Вторым шагом является сравнение простых множителей обоих чисел. Если числа имеют общие простые множители, то они не являются взаимно простыми. В данном случае мы видим, что числа 969 и 364 не имеют общих простых множителей.
Зная, что числа взаимно просты, мы можем применять их в различных математических операциях или задачах, не беспокоясь о делении на общие множители. Например, при решении уравнений или нахождении НОД или НОК чисел.
Зачем доказывать взаимную простоту чисел?
Одно из главных применений доказательства взаимной простоты чисел - это факторизация чисел. Если мы знаем, что два числа взаимно просты, то мы можем разложить их на простые множители и легко найти их НОК (наименьшее общее кратное) и НОД (наибольший общий делитель).
Взаимная простота чисел также является ключевым понятием в криптографии. Все современные алгоритмы шифрования используют большие простые числа, которые являются взаимно простыми со своими соседними числами. Это обеспечивает надежность и безопасность шифрования и защиту от взлома.
Доказательство взаимной простоты чисел также имеет значимость в комбинаторике и теории чисел. Оно помогает решать различные задачи, связанные с делением и разложением чисел на множители, нахождением остатков и суммы делителей числа.
Таким образом, доказательство взаимной простоты чисел играет важную роль в различных областях математики и науки в целом. Оно позволяет углубить понимание чисел и их взаимосвязей, а также применить полученные знания в практических задачах.
Применение взаимной простоты в криптографии и других областях

Одним из наиболее распространенных способов использования взаимной простоты в криптографии является алгоритм RSA (Rivest-Shamir-Adleman). Этот алгоритм использует два больших взаимно простых числа для генерации открытого и закрытого ключей. Открытый ключ используется для шифрования сообщений, а закрытый ключ - для их расшифровки. Благодаря свойству взаимной простоты, сложно обратно вычислить закрытый ключ, зная только открытый ключ.
Взаимная простота также применяется в области кодирования информации и проверки целостности данных. Например, в качестве контрольной суммы или хеш-функций используются числа, которые взаимно просты с основанием кодирования. Это позволяет обнаруживать ошибки в передаче данных или изменения данных.
Взаимная простота также находит применение в теории чисел, где она является одним из ключевых понятий. Исследование взаимной простоты чисел помогает при решении задач по разложению чисел на множители и нахождению простых чисел.
Таким образом, взаимная простота чисел является фундаментальным понятием, применяемым в криптографии, кодировании информации и теории чисел. Это свойство чисел обеспечивает безопасность и надежность в различных областях, где требуется обработка и передача конфиденциальной информации.



