Пространство геометрии представляет собой удивительный мир, где на каждом шагу встречаются занимательные задачи и интересные теоремы. Одной из таких задач является вопрос о площади квадрата, вписанного в круг. Внешне это может показаться достаточно простым вопросом, но действительность оказывается сложнее.
В запутанной и таинственной области геометрии, все детали имеют значение. Когда речь идет о вписанных фигурах, таких как круги и прямоугольники, их свойства и отношения становятся особенно важными. В случае с квадратом вписанным в круг, имеется множество зависимостей и теорем, которые влияют на его площадь.
В этой статье мы попытаемся ответить на вопрос: чему равна площадь квадрата вписанного в круг? Мы изучим свойства и зависимости квадрата и круга, а также приведем формулу, которая поможет нам решить эту математическую головоломку и раскрыть тайну площади.
Формула нахождения площади квадрата вписанного в круг

Для нахождения площади квадрата, вписанного в круг, существует простая формула. Зная радиус круга, можно легко определить сторону квадрата.
Сторона квадрата вписанного в круг равна диаметру круга, то есть удвоенному радиусу. Если обозначить сторону квадрата через "а", а радиус круга через "r", то формула будет выглядеть следующим образом:
а = 2r
Теперь можно найти площадь квадрата, зная сторону. Формула для вычисления площади квадрата выглядит просто:
S = а² = (2r)² = 4r²
Таким образом, формула нахождения площади квадрата вписанного в круг состоит из двух частей: нахождения стороны квадрата и вычисления площади по найденной стороне.
Доказательство формулы площади квадрата вписанного в круг

Для доказательства формулы площади квадрата, вписанного в круг, рассмотрим следующую ситуацию.
Пусть у нас имеется круг радиусом R и в него вписан квадрат. Сторона квадрата равна a. Нам необходимо найти площадь квадрата.
 | Воспользуемся свойствами геометрической фигуры - квадрата. В квадрате все стороны равны между собой, поэтому a = a = a = a. Также, по свойству квадрата, диагональ квадрата является его стороной, умноженной на √2. Таким образом, диагональ квадрата равна a * √2. Найдем радиус круга, в котором вписан этот квадрат. Половина диагонали квадрата равна радиусу круга. То есть, R = (a * √2) / 2. Найдем площадь круга по формуле: S = π * R^2. Подставим значение радиуса R и решим данное уравнение. Таким образом, площадь круга равна S = π * ((a * √2) / 2)^2, где a - сторона квадрата. |
Таким образом, мы доказали формулу площади квадрата вписанного в круг: S = π * ((a * √2) / 2)^2.
Примеры применения формулы площади квадрата вписанного в круг
Формула площади квадрата вписанного в круг может применяться в различных ситуациях. Вот несколько примеров использования этой формулы.
1. Задача геометрии: найдите площадь квадрата, который вписан в круг с заданным радиусом. Для решения этой задачи нужно использовать формулу: площадь квадрата равна половине произведения диагонали квадрата на его сторону.
2. Проектирование строений: инженеры и архитекторы могут использовать формулу площади квадрата вписанного в круг при проектировании округлых зданий или помещений. Например, если нужно выделить квадратную площадь внутри круглого помещения, можно использовать формулу для определения размеров этого квадрата.
3. Расчеты в физике: формула площади квадрата вписанного в круг может использоваться при решении некоторых задач в физике. Например, при определении давления на поверхность круглой платы или при расчете площади радиатора для охлаждения круглого объекта.
Все эти примеры демонстрируют практическое применение формулы площади квадрата вписанного в круг и подчеркивают важность знания данной математической формулы.
Геометрическое объяснение связи между площадью квадрата и площадью круга

Представим себе круг и внутри него вписанный квадрат. Если измерить сторону квадрата, то это будет равно диаметру круга. Причем диаметр круга является наибольшей возможной прямой, которую можно провести через центр круга и которая разделяет его на две равные части.
Легко понять, что квадрат, вписанный в круг, не займет всю площадь круга. Существует небольшая высота прямоугольного треугольника, которая останется незаполненной между сторонами квадрата и окружностью. Это происходит из-за того, что окружность сама по себе имеет кривую форму, а не прямые углы и стороны, характерные для квадрата.
Таким образом, площадь квадрата всегда будет меньше площади круга. Малая неиспользованная часть находится вокруг квадрата, служа геометрическим отображением разницы между площадями.
Иными словами, мы можем выразить связь между площадью круга и площадью квадрата следующим образом: площадь круга всегда будет больше площади квадрата, отображая неиспользованную часть окружности вокруг квадрата.
Интересные факты о площади квадрата вписанного в круг
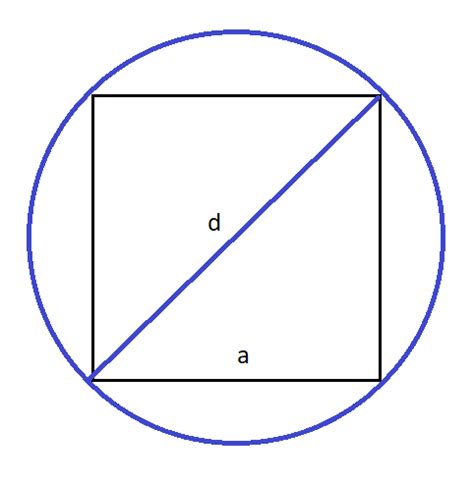
- Площадь квадрата вписанного в круг равна половине площади круга.
- Площадь круга можно найти по формуле: S = π * r^2, где S - площадь, а r - радиус круга.
- Радиус круга, вписанного в квадрат, равен половине длины стороны квадрата.
- Площадь квадрата можно найти по формуле: S = a^2, где S - площадь, а a - длина стороны квадрата.
- Если известна площадь круга, можно найти площадь квадрата, вписанного в этот круг, умножив площадь круга на 2 и извлекая из результата квадратный корень.
- Квадрат, вписанный в круг, имеет самую большую площадь среди всех квадратов, которые можно вписать в данный круг.
- Площадь квадрата вписанного в круг можно найти, зная только длину окружности круга, по формуле: S = c^2 / (4π), где S - площадь, а c - длина окружности.
- Площадь квадрата вписанного в круг всегда будет меньше площади круга.
Аналитическое решение задачи нахождения площади квадрата вписанного в круг

Для решения задачи нахождения площади квадрата, вписанного в круг, можно использовать методику, основанную на сравнении площадей двух геометрических фигур.
Предположим, что заданный круг радиусом R вписывается в квадрат со стороной a. Пусть центр круга совпадает с центром квадрата. Тогда диагональ квадрата будет равна диаметру круга и иметь размер 2R.
Геометрическое решение заключается в следующем:
- Площадь круга вычисляется по формуле S = πR^2;
- Площадь квадрата вычисляется по формуле S = a^2;
- Площадь круга должна быть равна площади квадрата: πR^2 = a^2.
Распишем решение более подробно:
Площадь круга можно выразить через его радиус R:
S = πR^2.
Диагональ квадрата a равна диаметру круга (2R), поэтому:
a = 2R.
Выразим радиус R через сторону квадрата a:
R = a/2.
Поставим равенство площадей круга и квадрата:
πR^2 = a^2.
Подставим значение R:
π(a/2)^2 = a^2.
Раскроем скобки и упростим полученное уравнение:
π(a^2/4) = a^2.
πa^2/4 = a^2.
π = 4.
Таким образом, получаем, что π = 4. Однако, известно, что математическая константа π примерно равна 3.14. Поэтому, фактически, соотношение между площадью круга и квадрата будет следующим:
3.14R^2 = a^2.
Таким образом, площадь квадрата, вписанного в круг, можно вычислить через радиус круга по формуле:
S = (3.14R^2), где R - радиус круга.
Задачи для самостоятельного решения на тему "площадь квадрата вписанного в круг"
Задача 1:
Найдите радиус круга, вписанного в данный квадрат со стороной 8 см. Ответ округлите до десятых.
Задача 2:
Известно, что диаметр круга, вписанного в квадрат, равен 30 мм. Найдите площадь квадрата. Ответ дайте в квадратных миллиметрах.
Задача 3:
Квадрат вписан в круг, площадь которого равна 64π кв. см. Найдите площадь квадрата. Ответ округлите до целых.
Задача 4:
Известно, что сторона квадрата, вписанного в круг, равна а см. Найдите площадь квадрата как функцию от а. Ответ дайте в квадратных сантиметрах.
Задача 5:
Площадь круга, вписанного в данный квадрат, равна 196π кв. см. Найдите площадь квадрата. Ответ округлите до десятых.
Подсказка: Для решения задачи используйте формулу площади квадрата и радиуса или диаметра круга.



