Алгебра – это раздел математики, который изучает алгебраические объекты и операции над ними. Восьмой класс – время, когда школьники начинают изучать более сложные концепции в алгебре, включая понятие периода. Период – это основное понятие, которое позволяет понять упорядоченность и повторяемость алгебраических выражений.
Период в алгебре может быть определен как минимальное положительное целое число n, такое, что для любого целого числа k, значение алгебраического выражения остается неизменным при замене аргумента x на x + n∙k. Другими словами, алгебраическое выражение имеет период n, если его значение повторяется через каждые n единиц аргумента.
Например, если у нас есть выражение f(x) = sin(x), то оно имеет период 2π, так как sin(x + 2π) = sin(x), где x – аргумент.
Что такое период в алгебре 8 класс?
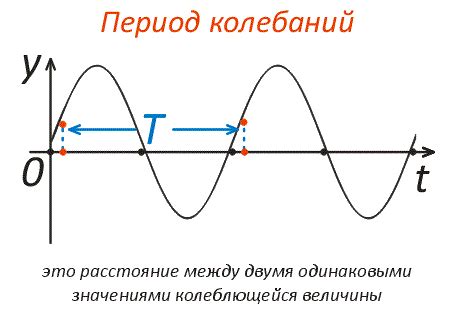
В алгебре 8 класса период обычно относится к теме функций и их особенностей. Период функции – это расстояние между двумя последовательными точками повторения паттерна в графике функции или в значении функции. Он применяется как для тригонометрических функций, так и для других типов функций, таких как логарифмические или показательные функции.
Период может быть представлен числом, которое указывает, через какие значения аргумента функции происходит повторение паттерна. Например, для синусоидальной функции, такой как y = sin(x), период равен 2π, что означает, что паттерн повторяется каждые 2π радиан.
Знание периода функции позволяет анализировать ее поведение и прогнозировать ее значения на определенных интервалах. Оно также позволяет решать уравнения и системы уравнений, связанные с повторяющимися паттернами функций.
В алгебре 8 класса изучаются как простые, так и более сложные функции с различными периодами. Понимание периода помогает учащимся лучше понять и использо
Определение понятия "период"
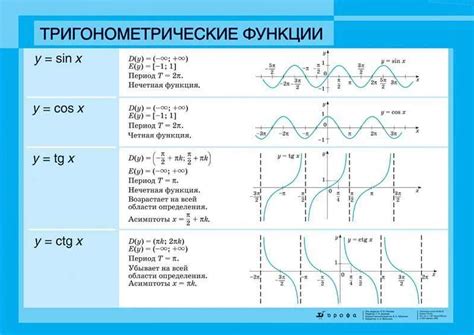
Для примера, пусть a = 2. При возведении числа 2 в натуральные степени получим: 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, 27 = 128, 28 = 256, 29 = 512, 210 = 1024, 211 = 2048, 212 = 4096, 213 = 8192, 214 = 16384, 215 = 32768, 216 = 65536, 217 = 131072, 218 = 262144, 219 = 524288, 220 = 1048576, 221 = 2097152, 222 = 4194304, 223 = 8388608, 224 = 16777216, 225 = 33554432, 226 = 67108864, 227 = 134217728, 228 = 268435456, 229 = 536870912, 230 = 1073741824, 231 = 2147483648, 232 = 4294967296, 233 = 8589934592, 234 = 17179869184, 235 = 34359738368, 236 = 68719476736, 237 = 137438953472, 238 = 274877906944, 239 = 549755813888, 240 = 1099511627776, 241 = 2199023255552, 242 = 4398046511104, 243 = 8796093022208, 244 = 17592186044416, 245 = 35184372088832, 246 = 70368744177664, 247 = 140737488355328, 248 = 281474976710656, 249 = 562949953421312, 250 = 1125899906842624, 251 = 2251799813685248, 252 = 4503599627370496, 253 = 9007199254740992, 254 = 18014398509481984, 255 = 36028797018963968, 256 = 72057594037927936, 257 = 144115188075855872, 258 = 288230376151711744, 259 = 576460752303423488, 260 = 1152921504606846976, 261 = 2305843009213693952, 262 = 4611686018427387904, 263 = 9223372036854775808, 264 = 18446744073709551616, 265 = 36893488147419103232, 266 = 73786976294838206464, 267 = 147573952589676412928, 268 = 295147905179352825856, 269 = 590295810358705651712, 270 = 1180591620717411303424, 271 = 2361183241434822606848, 272 = 4722366482869645213696, 273 = 9444732965739290427392, 274 = 18889465931478580854784, 275 = 37778931862957161709568, 276 = 75557863725914323419136, 277 = 151115727451828646838272, 278 = 302231454903657293676544, 279 = 604462909807314587353088, 280 = 1208925819614629174706176, 281 = 2417851639229258349412352, 282 = 4835703278458516698824704, 283 = 9671406556917033397649408, 284 = 19342813113834066795298816, 285 = 38685626227668133590597632, 286 = 77371252455336267181195264, 287 = 154742504910672534362390528, 288 = 309485009821345068724781056, 289 = 618970019642690137449562112, 290 = 1237940039285380274899124224, 291 = 2475880078570760549798248448, 292 = 4951760157141521099596496896, 293 = 9903520314283042199192993792, 294 = 19807040628566084398385987584, 295 = 39614081257132168796771975168, 296 = 79228162514264337593543950336, 297 = 158456325028528675187087900672, 298 = 316912650057057350374175801344, 299 = 633825300114114700748351602688, 2100 = 1267650600228229401496703205376, 2101 = 2535301200456458802993406410752, 2102 = 5070602400912917605986812821504, 2103 = 10141204801825835211973625643008, 2104 = 20282409603651670423947251286016, 2105 = 40564819207303340847894502572032, 2106 = 81129638414606681695789005144064, 2107 = 162259276829213363391578010288128, 2108 = 324518553658426726783156020576256, 2109 = 649037107316853453566312041152512, 2110 = 1298074214633706907132624082305024, 2111 = 2596148429267413814265248164610048, 2112 = 5192296858534827628530496329220096, 2113 = 10384593717069655257060992658440192, 2114 = 20769187434139310514121985316880384, 2115 = 41538374868278621028243970633760768, 2116 = 83076749736557242056487941267521536, 2117 = 166153499473114484112975882535043072, 2118 = 332306998946228968225951765070086144, 2119 = 664613997892457936451903530140172288, 2120 = 1329227995784915872903807060280344576, 2121 = 2658455991569831745807614120560689152, 2122 = 5316911983139663491615228241121378304, 2123 = 10633823966279326983230456482242756608, 2124 = 21267647932558653966460912964485513216, 2125 = 42535295865117307932921825928971026432, 2126 = 85070591730234615865843651857942052864, 2127 = 170141183460469231731687303715884105728, 2128 = 340282366920938463463374607431768211456, 2129 = 680564733841876926926749214863536422912, 2130 = 1361129467683753853853498429727072845824, 2131 = 2722258935367507707706996859454145691648, 2132 = 5444517870735015415413993718908291383296, 2133 = 10889035741470030830827987437816582766592, 2134 = 21778071482940061661655974875633165533184, 2135 = 43556142965880123323311949751266331066368, 2136 = 87112285931760246646623899502532662132736, 2137 = 174224571863520493293247799005065324265472, 2138 = 348449143727040986586495598010130648530944, 2139 = 696898287454081973172991196020261297061888, 2140 = 1393796574908163946345982392040522594123776, 2141 = 2787593149816327892691964784081045188247552, 2142 = 5575186299632655785383929568162090376495104, 2143 = 11150372599265311570767859136324180752990208, 2144 = 22300745198530623141535718272648361505980416, 2145 = 44601490397061246283071436545296723011960832, 2146 = 89202980794122492566142873090593446023921664, 2147 = 178405961588244985132285746181186892047843328, 2148 = 356811923176489970264571492362373784095686656, 2149 = 713623846352979940529142984724747568191373312, 2150 = 1427247692705959881058285969449495136382746624, 2151 = 2854495385411919762116571938898990272765493248, 2152 = 5708990770823839524233143877797980545530986496, 2153 = 11417981541647679048466287755595961091061972992, 2154 = 22835963083295358096932575511191922182123945984, 2155 = 45671926166590716193865151022383844364247891968, 2156 = 91343852333181432387730302044767688728495783936, 2157 = 182687704666362864775460604089535377456991567872, 2158 = 365375409332725729550921208179070754913983135744, 2159 = 730750818665451459101842416358141509827966271488, 2160 = 146150163733090291820368483271628301
Период в алгебре: основные понятия

В алгебре, периодом называется наименьшее положительное число, для которого выполняется равенство:
an ≡ 1 (mod m),
где a и m - целые числа, n - натуральное число.
Период обозначается как ordm(a) или просто ord(a).
Период в алгебре имеет несколько важных свойств:
1. Период простого числа p для a, такого что НОД(a, p) = 1, равен p-1.
2. Если период для a равен t (ord(a) = t), то ak ≡ ak mod t (mod m)
3. Если ord(a) = t, то at ≡ 1 (mod m) и ad ≡ 1 (mod m), где d - делитель t.
4. Сумма периодов для двух чисел a и b равна наименьшему общему кратному их периодов.
Знание основных понятий и свойств периода в алгебре позволяет решать различные задачи, связанные с модульной арифметикой и теорией чисел.
Как вычислить период?

Период в алгебре используется для определения повторяющихся шаблонов в числовых последовательностях. Для вычисления периода необходимо следовать следующим шагам:
1. Найти первое число последовательности, которое повторяется. Обозначим его как а.
2. Найти следующее число, которое совпадает с а. Обозначим его как b.
3. Продолжать находить следующие числа последовательности, пока не найдется число, совпадающее с а.
4. Повторять шаги 2 и 3, пока не будут найдены все повторяющиеся числа и образован полный период последовательности.
Например, рассмотрим последовательность: 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, ...
Период данной последовательности составляет 5, так как повторяющийся шаблон состоит из 5 чисел: 0, 1, 2, 3, 4.
Вычисление периода позволяет увидеть закономерности в повторяющихся числовых последовательностях и использовать их для последующих вычислений и задач в алгебре.
Примеры вычисления периода
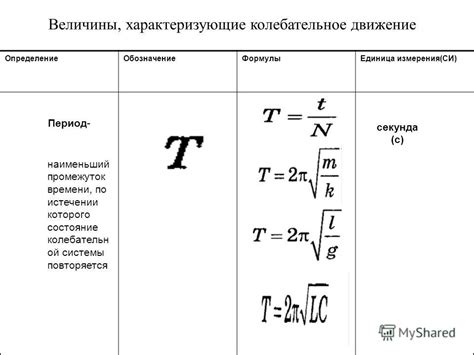
Для наглядности рассмотрим несколько примеров вычисления периода функции:
| Пример | Функция | Период |
|---|---|---|
| 1 | f(x) = sin(x) | π |
| 2 | f(x) = cos(2x) | π |
| 3 | f(x) = 2sin(3x) | π/3 |
| 4 | f(x) = tan(x) | π |
В первом примере функция sin(x) имеет период π, что означает, что она повторяется каждые π радиан. Во втором примере функция cos(2x) также имеет период π. При увеличении аргумента функции в два раза, период не меняется. В третьем примере функция 2sin(3x) имеет период π/3. Здесь аргумент функции увеличен в три раза и период сократился в три раза. В четвёртом примере функция tan(x) также имеет период π.
Периодический остаток и периодическая десятичная дробь
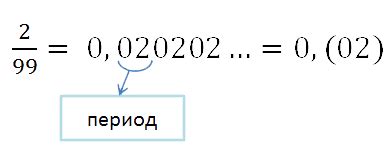
Периодическая десятичная дробь – это десятичная дробь, в которой есть периодический остаток. Период может быть составлен из одной или нескольких цифр, которые повторяются бесконечно.
Например, число 1/3, в десятичной форме, будет выглядеть как 0,3333333... Здесь тройка будет повторяться бесконечно, что и даёт нам понять, что число 1/3 – периодическая десятичная дробь.
Периодическая десятичная дробь также может быть представлена в виде обыкновенной дроби. В случае с 1/3, это будет выглядеть как 1/3 = 0,3333333... = 0.(3).
Изучение периодических остатков и периодических десятичных дробей позволяет нам понять, как работает система десятичной записи чисел и решать различные задачи связанные с этой темой.
Свойства периодической десятичной дроби

Основные свойства периодической десятичной дроби:
- Периодическая десятичная дробь может быть представлена в виде обыкновенной дроби. Для этого ненулевую часть следует записать без разделительной точки, а период после разделительной точки записать в виде дроби с числителем, равным периоду, и знаменателем, состоящим из единицы, соответствующей количеству цифр в периоде.
- Периодическая десятичная дробь равна сумме её ненулевой части и бесконечной десятичной дроби, в которой все цифры равны периоду. Например, дробь 0,333... равна 0,3 + 0,03 + 0,003 + ... и может быть записана как 1/3.
- Периодическая десятичная дробь может быть преобразована в окончательную десятичную дробь путем составления уравнения и решения. Например, для дроби 0,484848... можно записать уравнение 100x = 48,4848..., где x - искомая дробь. После решения уравнения получим, что x = 48/99, что равно 16/33.
Изучение свойств периодических десятичных дробей позволяет решать задачи связанные с операциями над такими дробями, а также исследовать их свойства и взаимосвязи с обыкновенными дробями.
Периоды в рациональных числах и иррациональных числах

Период в рациональном числе - это последовательность одинаковых цифр, которая повторяется бесконечно после запятой. Например, число 1/3 представлено в десятичном виде как 0.3333..., где 3 - это период. Это означает, что после запятой последовательность цифр 3 будет повторяться бесконечно.
Иррациональные числа - это числа, которые не могут быть представлены в виде дроби. Иррациональные числа не имеют периодов в своих десятичных представлениях. Например, число π (пи) является иррациональным числом и его десятичное представление бесконечное и не имеет периода.
Периоды в рациональных числах могут быть использованы для расчетов и анализа постоянных десятичных последовательностей. Они также могут быть использованы для определения периодичности чисел и создания математических моделей.
Периоды в рациональных числах и иррациональных числах являются важными понятиями в алгебре и математике, которые помогают нам понять и анализировать различные типы чисел.



