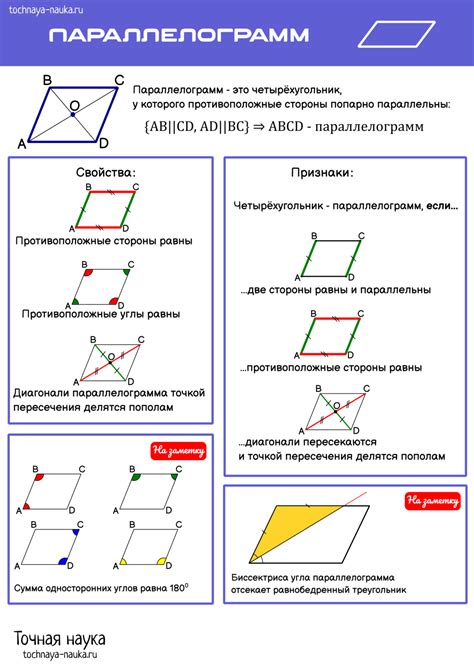
Параллелограмм - это особый тип четырехугольника, который имеет ряд уникальных свойств и признаков. Этот геометрический объект привлекает внимание и изучается в школе и вузе, а также в множестве научных и практических областей.
Основным свойством параллелограмма является то, что противоположные стороны этой фигуры параллельны друг другу. Также очевидно, что соседние стороны параллелограмма равны и противоположные углы равны между собой. Эти свойства являются основой для доказательства других утверждений и теорем, связанных с параллелограммами.
Параллелограммы имеют несколько важных признаков. Во-первых, если стороны параллелограмма равны между собой, то такая фигура называется ромбом. Если же стороны параллелограмма перпендикулярны, то это квадрат. Кроме того, в параллелограмме сумма двух соседних углов всегда равна 180 градусов, а диагонали этой фигуры делятся пополам.
Параллелограммы находят широкое применение в различных областях: архитектуре, инженерии, физике, геодезии и т.д. Изучение свойств и признаков этой фигуры помогает решать различные математические задачи, а также позволяет лучше понять структуру и взаимосвязь геометрических объектов.
Параллелограмм: определение и признаки
Определение:
У параллелограмма есть следующие свойства:
- Противоположные стороны параллельны и равны.
- Противоположные углы параллельны и равны.
- Сумма углов в параллелограмме равна 360 градусов.
- Диагонали параллелограмма делятся пополам.
- Противоположные диагонали параллелограмма равны.
Признаки:
На плоскости можно определить, является ли данный четырехугольник параллелограммом, используя следующие признаки:
- Если противоположные стороны четырехугольника равны, то это параллелограмм.
- Если противоположные углы четырехугольника равны, то это параллелограмм.
- Если параллельные стороны четырехугольника равны, то это параллелограмм.
Если выполняется хотя бы один из этих признаков, то четырехугольник можно считать параллелограммом.
Описание и определение параллелограмма

Свойства параллелограмма:
| 1. Противоположные стороны параллельны |
| 2. Противоположные стороны равны по длине |
| 3. Противоположные углы равны |
| 4. Диагонали параллелограмма делятся пополам |
| 5. Сумма углов параллелограмма равна 360 градусов |
Чтобы определить, что данный четырехугольник является параллелограммом, необходимо проверить соответствие вышеперечисленных свойств. Если все они выполняются, то четырехугольник можно назвать параллелограммом.
Свойства параллелограмма
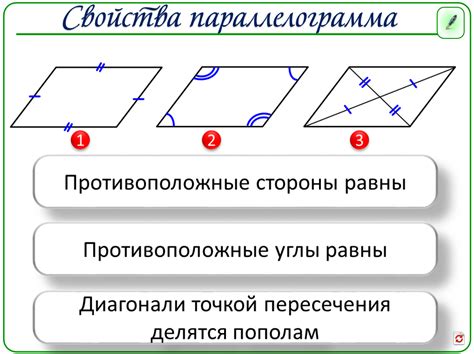
- Противоположные стороны параллелограмма равны и параллельны. Это означает, что если стороны AB и CD параллельны, то они имеют одинаковую длину.
- Противоположные углы параллелограмма равны. Например, если угол ABC равен углу CDA, то угол ABD будет равен углу BCD.
- Диагонали параллелограмма делятся пополам. Если AC и BD – диагонали параллелограмма, то точка их пересечения M будет серединой каждой из них.
- Сумма углов параллелограмма равна 360 градусов. То есть, угол ABC + угол BCD + угол CDA + угол DAB равна 360°.
- Если вершина параллелограмма A или C принадлежат окружности с диаметром BD, то угол ABC и угол CDA являются прямыми углами.
Из этих свойств вытекает множество других признаков и формул, которые помогают решать задачи, связанные с параллелограммами, в геометрии.
Признаки параллелограмма
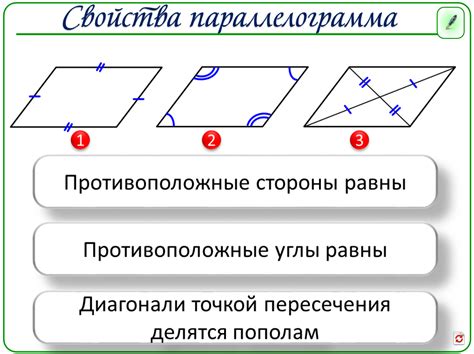
1. Противоположные стороны параллельны: В параллелограмме каждая сторона параллельна противоположной стороне. Это значит, что прямые, содержащие эти стороны, никогда не пересекаются.
2. Противоположные стороны равны по длине: В параллелограмме каждая сторона равна по длине своей противоположной стороне. Это означает, что соответствующие стороны имеют одинаковую меру.
3. Диагонали делятся пополам: В параллелограмме диагонали делятся пополам. Это значит, что точка их пересечения делит каждую диагональ на две равные части.
4. Противоположные углы равны: В параллелограмме каждый противоположный угол равен своему противоположному углу. Это означает, что углы, расположенные напротив друг друга, имеют одинаковую величину.
Равнобедренность и равноугольность параллелограмма
Равнобедренность параллелограмма означает, что две противоположные стороны параллелограмма имеют одинаковую длину. Это значит, что у параллелограмма можно найти две пары равных сторон.
Равноугольность параллелограмма означает, что все углы внутри фигуры равны между собой. Все углы параллелограмма являются прямыми, то есть равны 90 градусам.
Для наглядного представления свойств параллелограмма можно использовать таблицу:
| Свойство | Описание |
|---|---|
| Противоположные стороны параллельны | Две противоположные стороны параллелограмма расположены параллельно друг другу. |
| Равнобедренность | У параллелограмма две пары равных сторон. |
| Равноугольность | Все углы параллелограмма равны между собой и составляют 90 градусов. |
Теорема о сумме углов параллелограмма

Теорема о сумме углов параллелограмма утверждает, что сумма всех углов в параллелограмме равна 360 градусов.
Доказательство этой теоремы достаточно простое. Рассмотрим параллелограмм ABCD. Продлим сторону AB и BC до их пересечения в точке E. Таким образом, получим треугольник ECD.
Поскольку сторона AB параллельна стороне CD, угол ABD будет равен углу CDE, поскольку они являются соответственными углами, образованными параллельными прямыми AB и CD. Аналогично, угол ABC будет равен углу CED.
Так как в треугольнике ECD сумма углов всегда равна 180 градусов, то получаем, что углы ABD, ABC, CED и CDE в параллелограмме ABCD образуют сумму 180 градусов.
Также, учитывая, что в параллелограмме сумма противоположных углов равна 180 градусов, можно заключить, что сумма углов ABD, ABC, BCD и CDA также равна 180 градусов.
Таким образом, сумма всех углов в параллелограмме ABCD равна сумме углов треугольника ECD, то есть 180 + 180 = 360 градусов.
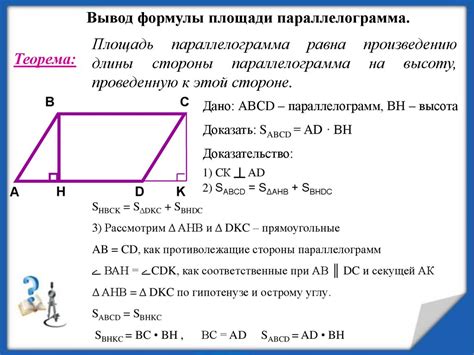
Площадь параллелограмма и методы ее вычисления

Первый метод для вычисления площади параллелограмма основан на использовании длины сторон и высоты. Для этого необходимо знать длину двух сторон параллелограмма и высоту, опущенную на одну из этих сторон. Площадь параллелограмма рассчитывается по формуле:
| S = a * h |
где S - площадь параллелограмма, a - длина одной из сторон, h - высота, опущенная на эту сторону.
Второй метод для вычисления площади параллелограмма основан на использовании векторов. Для этого нужно знать координаты вершин параллелограмма и использовать формулу:
| S = |(x1*y2 + x2*y3 + x3*y4 + x4*y1) - (y1*x2 + y2*x3 + y3*x4 + y4*x1)| / 2 |
где S - площадь параллелограмма, x1, y1, x2, y2, x3, y3, x4, y4 - координаты вершин параллелограмма.
Третий метод для вычисления площади параллелограмма основан на использовании базового векторного произведения. Для этого необходимо знать координаты вершин параллелограмма и использовать формулу:
| S = |(x1*y2 + x2*y3 + x3*y4 + x4*y1) - (x2*y1 + x3*y2 + x4*y3 + x1*y4)| / 2 |
где S - площадь параллелограмма, x1, y1, x2, y2, x3, y3, x4, y4 - координаты вершин параллелограмма.
Используя эти методы, можно вычислить площадь параллелограмма и получить точные результаты. Знание площади параллелограмма позволяет проводить дальнейшие геометрические вычисления и решать задачи, связанные с этой фигурой.



