Параллелограмм - одна из самых основных фигур в геометрии. Он представляет собой четырехугольник, у которого противоположные стороны параллельны и равны друг другу. В данной статье мы рассмотрим доказательство параллельности сторон параллелограмма kpht и авсд.
Для начала, давайте вспомним основные свойства параллелограмма. В параллелограмме противоположные стороны равны и параллельны. Исходя из этого, мы можем сделать предположение, что сторона kpht параллельна стороне авсд.
Чтобы доказать данное предположение, воспользуемся двумя методами: 1) доказательство параллельности с помощью соответствующих углов, 2) доказательство параллельности с помощью прямых и перпендикуляров.
Для доказательства первого метода, обратим внимание на соответствующие углы при параллельных сторонах. Если углы параллельных сторон kpht и авсд равны, то это будет одно из основных свойств параллелограмма, подтверждающее параллельность данных сторон. Следовательно, сторона kpht параллельна стороне авсд.
Определение параллелограмма
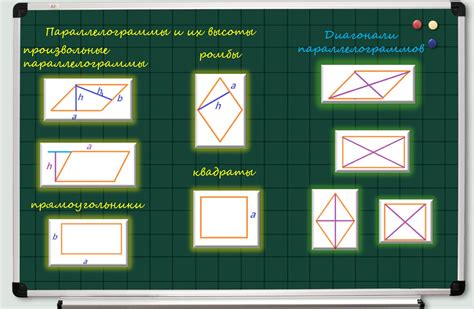
Другими словами, параллелограмм – это многоугольник с двумя парами параллельных сторон. Эти стороны называются основаниями параллелограмма, а остальные две его стороны – боковыми сторонами.
| Свойства параллелограмма: | Противоположные стороны параллельны. |
| Противоположные стороны равны. | |
| Свойства параллелограмма: | Сумма углов параллелограмма равна 360°. |
| Противоположные углы параллелограмма равны. |
Свойства сторон параллелограмма

- Стороны параллелограмма являются парами сторон, которые расположены противоположно друг другу. Их длины равны.
- Противоположные стороны параллелограмма параллельны и имеют одинаковые направления.
- Сумма двух сторон параллелограмма всегда больше третьей стороны.
- Стороны параллелограмма не могут пересекаться и образовывать угол, не равный 180 градусов.
- Каждая сторона параллелограмма является диагональю для одного из углов параллелограмма.
- Диагонали параллелограмма делятся пополам и пересекаются в центре параллелограмма.
Знание основных свойств сторон параллелограмма очень полезно при решении задач и доказательств, связанных с этой фигурой.
Углы в параллелограмме
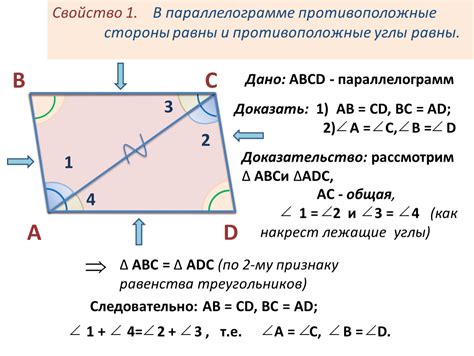
1. Противоположные углы параллелограмма равны. То есть, если угол А равен углу С, то угол В равен углу D.
2. Сумма углов параллелограмма всегда равна 360 градусов. Это следует из того, что противоположные углы параллельных сторон образуют пары смежных углов, которые в сумме дают 180 градусов. А так как параллелограмм имеет две пары параллельных сторон и каждая пара образует по два смежных угла, то сумма углов будет равна 180 + 180 = 360 градусов.
3. Диагонали параллелограмма делят его на два равных треугольника. Если провести диагонали параллелограмма, то они разделят фигуру на два равных треугольника. Каждый треугольник получится по половине от параллелограмма, а значит углы в них также будут равны.
4. Угол между диагоналями параллелограмма прямой. Диагонали параллелограмма пересекаются в точке О. Угол между диагоналями, то есть угол ВОА или угол ВОС, является прямым.
Данные особенности углов помогают нам лучше понять свойства и характеристики параллелограмма. На их основе можно строить доказательства или решать задачи, связанные с этой фигурой.
Свойства диагоналей параллелограмма
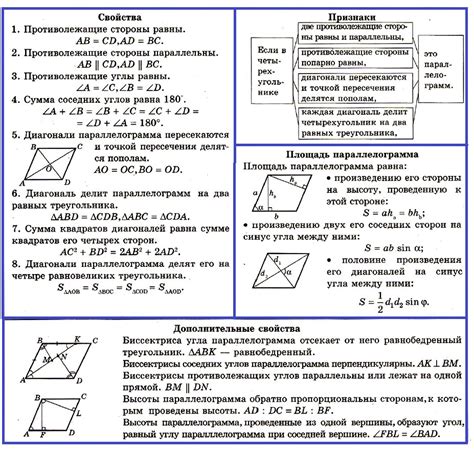
Диагонали параллелограмма - это отрезки, соединяющие противолежащие вершины. Они имеют ряд важных свойств:
- Диагонали параллелограмма делят его на два равных треугольника. То есть, каждая диагональ делит параллелограмм на две половины, которые по площади равны.
- Диагонали параллелограмма пересекаются в точке, которая является серединой каждой из диагоналей. То есть, точка пересечения диагоналей делит каждую диагональ пополам.
- Длина каждой диагонали параллелограмма равна сумме длин двух его сторон, и они делятся ее делением пополам. То есть, если a и b - длины сторон, а d - длина диагонали, то d = √(a² + b²).
Доказательство параллельности сторон kpht

Для доказательства параллельности сторон kpht в параллелограмме требуется использование свойств данной фигуры.
Основным свойством параллелограмма является то, что противоположные стороны данной фигуры параллельны. Таким образом, чтобы доказать параллельность сторон kpht, достаточно доказать параллельность одной из соседних сторон параллелограмма.
Рассмотрим сторону kp. Для доказательства параллельности этой стороны можно использовать следующие свойства:
- Параллельные прямые имеют равные углы с пересекающей их прямой. В параллелограмме kpht, сторона kp параллельна стороне ht и пересекается сторонами kh и pt. Следовательно, углы k и h равны, и углы p и t также равны.
- Параллельные прямые имеют равные углы с прямыми, пересекающими их. В параллелограмме kpht, сторона kp параллельна стороне ht и пересекается прямыми, проходящими через точки k и p (соответственно) и пересекающими стороны kh и pt (соответственно). Следовательно, углы k и h равны, и углы p и t также равны.
Доказательство параллельности сторон авсд
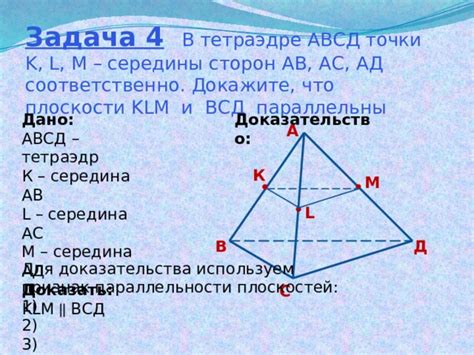
Для доказательства параллельности сторон авсд в параллелограмме kpht, мы можем использовать свойства параллелограмма и геометрические теоремы.
Для начала, вспомним основное свойство параллелограмма - противоположные стороны параллельны и равны. Из этого свойства следует, что сторона ав параллельна стороне сд в параллелограмме kpht.
Далее, вспомним теорему о параллельных прямых, которая гласит: если две прямые пересекаются третьей прямой так, что внутренние соответственные углы равны, то эти две прямые параллельны.
Используя эту теорему, мы можем доказать параллельность стороны ав стороне sd в параллелограмме kpht. Для этого нам нужно доказать, что угол авс равен углу сдт или, другими словами, что соответственные углы авс и сдт равны.
Мы можем это сделать, заметив, что авс и сдт - параллельные прямые, которые пересекаются прямой ст. Следовательно, угол авс и угол сдт являются внутренними соответственными углами при пересечении прямых авс и сдт прямой ст.
Таким образом, мы доказали, что угол авс равен углу сдт, что означает, что соответственные углы авс и сдт равны. Следовательно, по теореме о параллельных прямых, сторона ав параллельна стороне сд в параллелограмме kpht.
Таким образом, мы доказали, что сторона ав параллельна стороне сд в параллелограмме kpht, что подтверждает параллельность сторон авсд в этом параллелограмме.
Использование свойств сторон и углов для доказательства

Доказательство параллельности сторон параллелограмма kpht и авсд можно осуществить с использованием свойств сторон и углов данной фигуры. Для этого необходимо учесть несколько важных фактов.
Во-первых, параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. Итак, мы знаем, что сторона kp



