Медиана, биссектриса и высота - это понятия, которые широко используются в геометрии и имеют важное значение при изучении треугольников.
Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Получается, что в треугольнике всегда три медианы - каждая проходит через одну из вершин и середину противоположной стороны.
Биссектриса - это отрезок, который делит угол треугольника на два равных угла. То есть биссектриса делит угол таким образом, что в каждом из получившихся углов содержится равное количество градусов.
Высота - это отрезок, который проходит через вершину треугольника и перпендикулярен к противоположной стороне. То есть высота образует прямой угол с этой стороной.
Таким образом, медиана, биссектриса и высота имеют разные определения. Они не только выполняют разные функции и имеют разные свойства, но и применяются в разных задачах и уравнениях. Понимание различий между ними позволяет более глубоко изучить геометрию треугольников.
Медиана: понятие и свойства
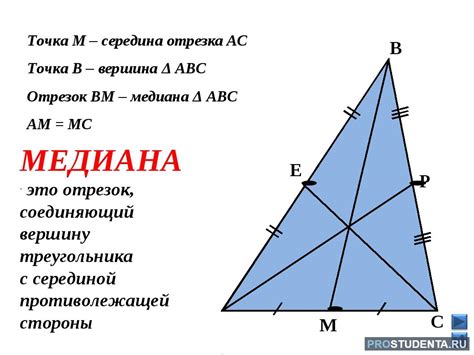
Медиана является отрезком, соединяющим вершину треугольника с серединой противоположной стороны. В треугольнике всегда существуют три медианы, каждая из которых имеет свои свойства.
Свойства медианы:
- Медиана делит стороны треугольника пополам. То есть, отрезок медианы, соединяющий вершину треугольника с серединой противоположной стороны, делит эту сторону на две равные части.
- Три медианы треугольника пересекаются в одной точке, называемой центром масс или точкой пересечения медиан. Эта точка делит каждую медиану в отношении 2:1. То есть, отрезок, соединяющий центр масс и вершину треугольника, в два раза длиннее отрезка, соединяющего центр масс и середину противоположной стороны.
- Центр масс треугольника совпадает с центром окружности, описанной вокруг этого треугольника. Это свойство медианы позволяет использовать ее для нахождения окружности, описанной вокруг треугольника.
Медиана является важным инструментом в решении многих геометрических задач. На основе свойств медианы можно вычислить площадь треугольника, найти его центр масс, а также определить окружность, описанную вокруг треугольника. Знание и понимание свойств медианы позволяет строить точные и эффективные геометрические модели и решать сложные задачи на плоскости.
Определение медианы
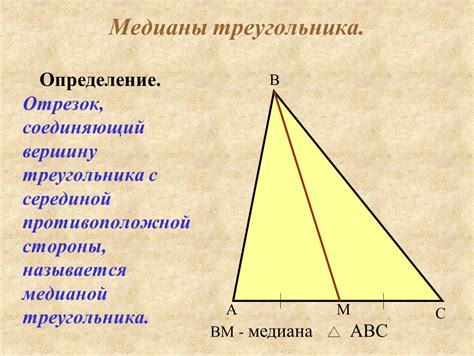
Медиана имеет ряд важных свойств:
- Медиана равна половине соответствующей стороны треугольника. Другими словами, длина медианы равна половине длины стороны, к которой она проведена.
- Медиана делит треугольник на два треугольника одинаковой площади. То есть, площадь треугольника, образованного медианой и соответствующей стороной, равна площади треугольника, образованного двумя другими сторонами треугольника.
- Медиана проходит через центр масс треугольника. Центр масс – точка пересечения медиан – является точкой баланса треугольника, где располагается центроид.
Медианы играют важную роль в геометрии треугольников и широко используются в решении различных задач, включая построение треугольников и нахождение центра масс.
Свойства медианы
- Медиана делит стороны треугольника пополам. То есть, отрезки, соединяющие вершину треугольника и середины противоположных сторон, равны по длине.
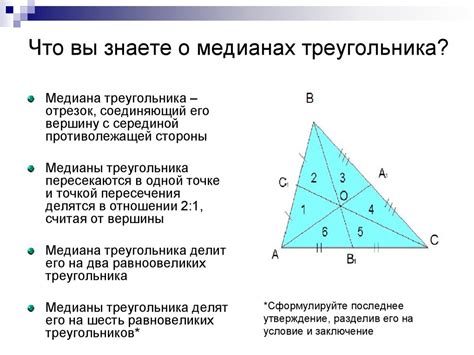
- Точка пересечения медиан называется центром тяжести треугольника. Она делит каждую медиану в отношении 2:1, то есть от вершины до центра тяжести две части отрезка равны, а одна – в два раза меньше.
- Медианы треугольника пересекаются в одной точке, которая называется центром тяжести. Это важное свойство, которое используется при решении многих геометрических задач.
- Медианы делят площадь треугольника на шесть равных частей.
- Если продолжить медиану за вершину треугольника на расстояние, равное половине стороны, она пересечет описанную окружность треугольника в диаметрально противоположной точке.
Медиана – важный элемент треугольника, который имеет множество свойств и применений в геометрии. Учитывая их, можно утверждать, что медиана является одним из основных структурных элементов треугольника и позволяет установить ряд зависимостей между его сторонами и углами.
Биссектриса: основные характеристики
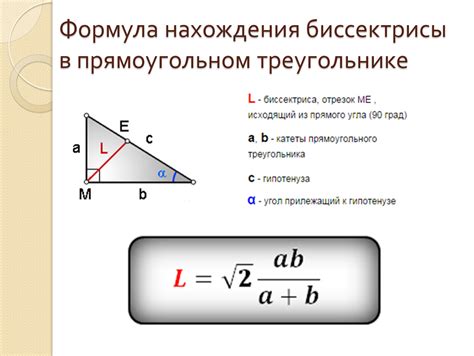
Основные характеристики биссектрисы:
- Биссектриса делит угол на два равных угла. Каждый из этих углов равен половине значения величины исходного угла.
- Биссектриса образует равные отрезки с противолежащими сторонами треугольника.
- Биссектриса пересекает прямую, соединяющую вершину угла с центром вписанной окружности в треугольнике.
- Точка пересечения биссектрисы с окружностью вписанного треугольника является центром окружности, вписанной в данный угол.
Биссектриса имеет важные приложения в геометрии, особенно в решении задач, связанных с треугольниками. Ее свойства и характеристики применяются для нахождения медианы, высоты, а также для определения других параметров треугольника.
Что такое биссектриса?
Биссектриса имеет особое значение в геометрии, так как она является одной из важных характеристик треугольника. Она проходит через вершину угла и делит противоположную сторону на две отрезка, с которыми отношение длин должно быть равно отношению длин других двух сторон треугольника.
Например: если биссектриса треугольника делит противоположную сторону на отрезки длиной 3 см и 5 см, а другие две стороны треугольника соответственно имеют длины 4 см и 6 см, то отношение 3:5 должно быть равно отношению 4:6.
Биссектриса также имеет отношение к другим элементам треугольника. Она перпендикулярна медиане, проходящей через середину противоположной стороны, а также к высоте, опущенной из вершины треугольника на противоположную сторону. Биссектриса делит все три эти линии в одной точке, называемой центром биссектрис треугольника.
Важные свойства биссектрисы
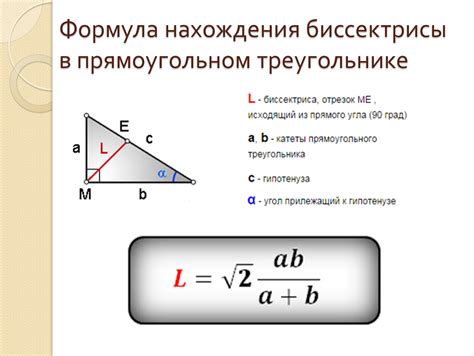
1. Равенство расстояний. Биссектриса угла равноудалена от его сторон. Это означает, что если провести перпендикулярные линии от точек пересечения биссектрисы с каждой стороной угла до самого угла (то есть до вершины), то получатся равные отрезки.
2. Равенство углов. Биссектриса угла разделяет его на два равных угла. Это значит, что каждый из этих двух новых углов будет иметь равные меры.
3. Взаимное пересечение. Биссектрисы двух смежных углов пересекаются в одной точке. Если у нас есть два смежных угла, то их биссектрисы пересекаются в одной точке, называемой центром биссектрисного пересечения.
Эти свойства делают биссектрису угла особо полезной в геометрических рассуждениях и задачах. Биссектриса помогает нам находить равные углы и определять расстояния до угла. Она играет важную роль в изучении треугольников и других фигур. Знание и понимание свойств биссектрисы позволяет решать задачи, связанные с углами и треугольниками более эффективно.



