Физический маятник и математический маятник – два понятия, которые широко используются в физике и математике для описания колебаний систем. Несмотря на схожие названия, эти два понятия имеют свои существенные различия и применяются в разных контекстах.
Физический маятник – это простая механическая система, состоящая из твердого тела, подвешенного на нити или стержне. При подвешивании маятника и его отклонении от положения равновесия, маятник начинает совершать колебания вокруг равновесного положения. Физический маятник можно встретить в повседневной жизни: например, часы с маятником или гиря в зале физкультуры.
Математический маятник – это абстрактная модель, которая используется в математике для анализа колебаний и расчетов. Математический маятник не имеет массы или конкретной формы, поэтому его можно рассматривать в виде абстрактного точечного объекта. Он используется, например, для изучения гармонических колебаний, а также в математических моделях, где конкретные значения не важны, но важно установление закономерностей и уровней энергии.
Таким образом, физический и математический маятники имеют свои отличия в том, что физический маятник – это реальный объект, имеющий массу и форму, а математический маятник – это абстрактная модель, используемая для анализа колебаний. Оба этих понятия важны для понимания принципов колебательных систем и нахождения математических закономерностей, поэтому они активно применяются в физике и математике.
Основные принципы движения маятников

Физический маятник - это тело, подвешенное на нити или стержне, которое свободно может колебаться вокруг точки подвеса. Движение физического маятника описывается гармоническими функциями, такими как синус и косинус.
Математический маятник - это абстрактная модель, используемая для моделирования движения маятников. Он не имеет массы и размеров, и его движение описывается математическими формулами.
Основные принципы движения маятников можно выразить следующими пунктами:
| Физический маятник | Математический маятник |
|---|---|
| Зависит от массы и длины нити или стержня. | Не имеет массы и размеров. |
| Движется с ускорением, зависящим от гравитационного поля. | Движется с ускорением, определяемым математической моделью. |
| Период колебаний зависит от длины нити или стержня и гравитационного поля. | Период колебаний определяется математической моделью. |
| Движение может быть амплитудным или затухающим. | Движение является амплитудным и идеализированным. |
Различия в уравнениях движения маятников
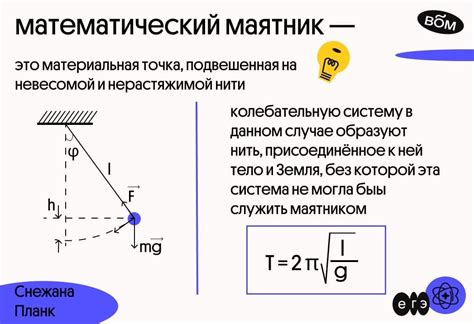
Уравнение движения физического маятника основано на законе Ньютона для вращательного движения. Оно выглядит следующим образом:
где:
θ - угол отклонения маятника от положения равновесия,
m - масса маятника,
L - длина маятника,
g - ускорение свободного падения.
Уравнение движения математического маятника, также известного как математический осциллятор или гармонический осциллятор, основывается на законе Гука для гармонического движения. Оно имеет вид:
где:
θ - угол отклонения маятника от положения равновесия,
k - коэффициент жесткости маятника,
m - масса маятника,
t - время.
Из уравнения движения физического маятника можно получить дифференциальное уравнение второго порядка, которое описывает его колебания. В то же время, уравнение движения математического маятника уже является дифференциальным уравнением второго порядка.
Эти уравнения имеют различные решения и могут использоваться для различных целей. Уравнение движения физического маятника позволяет описать его колебания с учетом силы трения и других физических факторов. В то время как уравнение движения математического маятника является идеализацией без учета таких факторов, что делает его более простым для решения и анализа.





