Треугольник abc - это одна из основных геометрических фигур, имеющая три стороны и три угла. У треугольника есть множество свойств и особенностей, которые делают его интересным объектом изучения для математиков и физиков.
Во-первых, треугольник abc может быть различных типов, в зависимости от длин сторон и величины углов. Например, если все стороны треугольника равны, то он называется равносторонним треугольником. Если две стороны равны, то треугольник называется равнобедренным. Если все стороны различны, то треугольник является разносторонним.
Во-вторых, треугольник abc имеет три угла - угол a, угол b и угол c. Сумма величин углов треугольника всегда равна 180 градусам. Это называется суммой углов треугольника и является одним из его важных свойств. Также, существует теорема, которая утверждает, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Треугольник abc также может быть использован в различных математических задачах и задачах эвристики. Его свойства и особенности могут быть применены в геометрии, алгебре, геодезии и других областях науки. Изучение треугольника abc позволяет лучше понять пространственную геометрию и взаимосвязь между его сторонами и углами.
Свойства треугольника abc
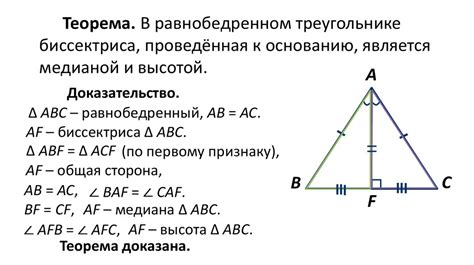
Стороны треугольника:
Сторона a - это отрезок, соединяющий вершины b и c.
Сторона b - это отрезок, соединяющий вершины a и c.
Сторона c - это отрезок, соединяющий вершины a и b.
Углы треугольника:
В треугольнике abc есть три угла: угол a, угол b и угол c. Сумма всех углов треугольника всегда равна 180 градусов.
Высоты треугольника:
Высота треугольника - это отрезок, перпендикулярный стороне треугольника и проведенный от вершины до основания. В треугольнике abc можно провести три высоты: высоту, опущенную из вершины a на сторону bc, высоту, опущенную из вершины b на сторону ac, и высоту, опущенную из вершины c на сторону ab.
Площадь треугольника:
Площадь треугольника можно найти, используя формулу Герона: S = √(p(p-a)(p-b)(p-c)), где p - полупериметр треугольника, a, b, c - длины сторон треугольника.
Также площадь можно вычислить как половину произведения длин двух сторон на синус угла между ними: S = (1/2)*(a*b)*sin(угол c).
Теорема Пифагора:
Если треугольник abc является прямоугольным, то выполняется теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы. Для прямоугольного треугольника это будет выглядеть следующим образом: a² + b² = c².
Таким образом, зная свойства треугольника abc, мы можем проводить различные вычисления и рассчитывать его характеристики.
Определение и структура

Структура треугольника определяется его сторонами и углами. Каждая сторона треугольника обозначается буквами, например, AB, BC, CA, где A, B и C - вершины треугольника. Углы треугольника также обозначаются буквами, например, ∠ABC, ∠BCA, ∠CAB, где A, B и C - вершины треугольника.
| Структура треугольника | Описание |
|---|---|
| Стороны | Отрезки, образующие границу треугольника |
| Вершины | Точки, образующие углы треугольника |
| Углы | Интервалы между сторонами треугольника |
Знание определения и структуры треугольника является основой для изучения его свойств и особенностей.
Основные характеристики

Основные характеристики треугольника включают:
| Стороны треугольника | Треугольник имеет три стороны, обозначаемые символами a, b и c. Длины сторон могут быть одинаковыми или разными. |
| Углы треугольника | Треугольник имеет три угла, обозначаемые символами A, B и C. Сумма углов треугольника всегда равна 180 градусам. |
| Периметр треугольника | Периметр треугольника - это сумма длин всех его сторон. Обозначается символом P. |
| Площадь треугольника | Площадь треугольника может быть вычислена различными способами, в зависимости от имеющихся данных. Обозначается символом S. |
| Высоты треугольника | Высоты треугольника - это отрезки, проведенные из вершин треугольника к противоположным сторонам. Определение высоты треугольника зависит от типа треугольника. |
| Медианы треугольника | Медианы треугольника - это отрезки, соединяющие вершины треугольника с серединами противоположных сторон. |
| Биссектрисы треугольника | Биссектрисы треугольника - это отрезки, делящие углы треугольника пополам. |
| Окружность, вписанная в треугольник | Окружность, вписанная в треугольник, касается всех трех сторон треугольника. Ее центр называется центром вписанной окружности. |
| Окружность, описанная около треугольника | Окружность, описанная около треугольника, проходит через все три вершины треугольника. Ее центр называется центром описанной окружности. |
Типы треугольников по длинам сторон
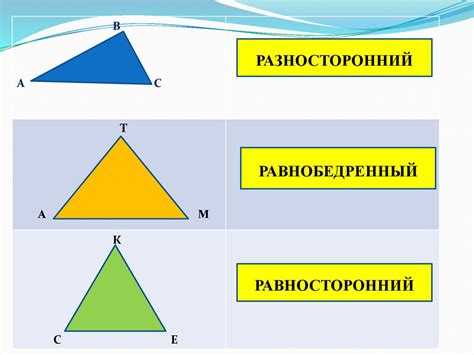
Существует несколько типов треугольников, которые можно классифицировать по длинам сторон:
1. Равносторонний треугольник:
В равностороннем треугольнике все стороны и углы равны между собой. Он имеет три равных стороны и три равных угла, каждый из которых равен 60 градусам.
2. Равнобедренный треугольник:
Равнобедренный треугольник имеет две равные стороны и два равных угла. Он может быть как с двумя равными сторонами и углами при основании, так и с двумя равными сторонами и углами при вершине.
3. Разносторонний треугольник:
Разносторонний треугольник имеет все три стороны разной длины. Он не имеет равных углов.
Знание типов треугольников по длинам сторон позволяет нам определить некоторые свойства и особенности каждого из них, а также применять соответствующие формулы для вычисления площади, периметра и других параметров треугольника.
Типы треугольников по углам
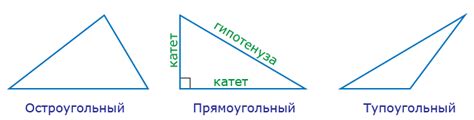
В зависимости от значений углов треугольников, их можно разделить на несколько типов:
- Остроугольный треугольник - треугольник, у которого все углы острые (имеют значение меньше 90 градусов).
- Тупоугольный треугольник - треугольник, у которого один угол тупой (имеет значение больше 90 градусов).
- Прямоугольный треугольник - треугольник, у которого один угол прямой (равен 90 градусов).
Знание типов треугольников по углам помогает определить их геометрические свойства и решать задачи в геометрии.



