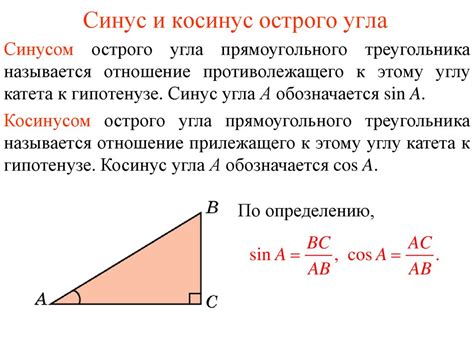
Прямоугольный треугольник – одна из самых известных и интересных фигур в геометрии. Его особенностью является наличие одного прямого угла, то есть угла, равного 90 градусам. Однако, помимо прямого угла, в прямоугольном треугольнике всегда присутствуют также два острых угла.
Острый угол в прямоугольном треугольнике всегда будет находиться напротив прямого угла. Это свойство обусловлено основной теоремой геометрии – теоремой Пифагора. По этой теореме, квадрат гипотенузы (стороны, лежащей напротив прямого угла) равен сумме квадратов катетов (сторон, прилегающих к прямому углу). А так как катеты не могут быть отрицательными, али дробями или равными нулю значениями, то они всегда будут меньше гипотенузы, и углы при их основаниях будут острыми.
То есть в прямоугольном треугольнике острые углы всегда будут острыми, несмотря на то, что их величина может быть различной. Важно отметить, что сумма углов любого треугольника всегда равна 180 градусам, поэтому сумма прямого угла и двух острых углов в прямоугольном треугольнике тоже будет равна 180 градусам.
Острый угол в прямоугольном треугольнике

Острый угол, также известный как аккут, определяется как угол, который меньше 90 градусов. Угол в прямоугольном треугольнике, который находится напротив прямого угла, называется противоположным острому углу.
Острый угол в прямоугольном треугольнике может быть вычислен с использованием тригонометрических функций, таких как синус, косинус и тангенс. Например, если известны длины противоположного и прилежащего к прямому углу катетов, острый угол может быть найден с использованием функции арктангенс.
Понимание острого угла в прямоугольном треугольнике важно в геометрии и тригонометрии, так как они помогают в решении задач, связанных с треугольниками и другими геометрическими фигурами. Острый угол является основой для вычислений, связанных с прямоугольными треугольниками, и может быть использован для нахождения длины сторон и других значений треугольника.
Определение острого угла
В прямоугольном треугольнике всегда есть один прямой угол, равный 90 градусов. Оставшиеся два угла всегда являются острыми.
Острый угол в прямоугольном треугольнике может быть измерен с помощью геометрических инструментов или вычислен с использованием математических формул, в зависимости от известных данных о длинах сторон треугольника.
Острый угол играет важную роль в прямоугольном треугольнике, так как определяет его форму и свойства. Например, величина острого угла влияет на длину гипотенузы и длины других сторон треугольника.
Свойства острого угла
Острый угол в прямоугольном треугольнике обладает рядом свойств:
- Значение острого угла всегда лежит в интервале от 0° до 90°. Он всегда меньше прямого угла.
- Острый угол можно обозначить любой буквой, но в математике часто используют греческую букву "α" (альфа), чтобы обозначить острый угол.
- Острый угол всегда противолежит наибольшей из сторон треугольника. Например, если стороны треугольника обозначены как a, b и c, где c - наибольшая сторона, то острый угол противолежит стороне c.
- Значение острого угла зависит от длин сторон треугольника, и между этими величинами существует соотношение, называемое теоремой синусов.
Знание свойств острого угла в прямоугольном треугольнике очень полезно для решения задач и вычислений, связанных с данным геометрическим объектом.
Тригонометрические функции острого угла

Одной из основных задач тригонометрии является нахождение значений тригонометрических функций острого угла. В частности, рассматриваются следующие тригонометрические функции:
- Синус (sin α) - отношение противолежащего катета к гипотенузе треугольника.
- Косинус (cos α) - отношение прилежащего катета к гипотенузе треугольника.
- Тангенс (tg α или tan α) - отношение противолежащего катета к прилежащему катету треугольника.
- Котангенс (ctg α или cot α) - отношение прилежащего катета к противолежащему катету треугольника.
- Секанс (sec α) - отношение гипотенузы к прилежащему катету треугольника.
- Косеканс (cosec α или csc α) - отношение гипотенузы к противолежащему катету треугольника.
Зная размеры двух сторон прямоугольного треугольника, можно вычислить значения этих тригонометрических функций острого угла.
Тригонометрические функции острого угла широко применяются в различных областях, включая физику, геометрию, инженерию и другие науки. Они позволяют решать множество задач, связанных с измерением и пропорциями треугольников.
Острый угол и противоположная сторона
В прямоугольном треугольнике острый угол считается одним из трех углов, и он всегда находится напротив наибольшей стороны треугольника.
Противоположная сторона к острому углу является наибольшей стороной треугольника. Именно ей соответствует острый угол.
Из свойства прямоугольного треугольника следует, что сумма всех углов равна 180 градусам. При этом острый угол может иметь любую величину от 0 до 90 градусов включительно.
Зная значение одного из углов прямоугольного треугольника, можно найти значения остальных углов, используя свойство их суммы.
Острый угол в прямоугольном треугольнике имеет важное значение для решения различных геометрических задач и формул.
Соотношения между острыми углами в прямоугольном треугольнике
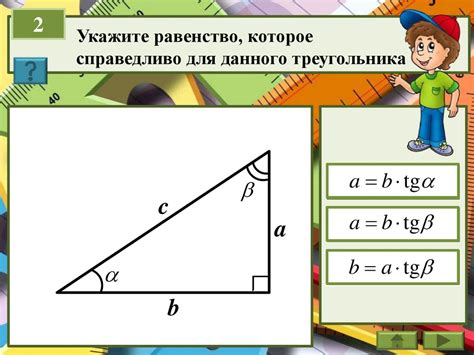
Сумма всех углов в треугольнике равна 180 градусам. Поэтому, если один из углов равен 90 градусам, то сумма двух острых углов также должна быть равна 90 градусам, чтобы общая сумма углов в треугольнике была равна 180 градусам.
Таким образом, в прямоугольном треугольнике сумма острых углов всегда равна 90 градусам, а каждый из острых углов меньше 90 градусов.
Проиллюстрируем это соотношение с помощью таблицы:
| Угол | Размер угла |
|---|---|
| Прямой угол | 90° |
| Острый угол 1 | меньше 90° |
| Острый угол 2 | меньше 90° |
Нахождение острого угла при известных сторонах

Прямоугольный треугольник, как следует из его названия, имеет один прямой угол, равный 90 градусам. Острый угол в таком треугольнике обозначается как α и остается неизвестным. Острый угол можно найти, зная длины противолежащей и прилежащей ему сторон.
Для решения этой задачи можно воспользоваться теоремой синусов или теоремой косинусов. Воспользуемся теоремой косинусов, так как она позволяет найти острый угол, зная длины всех сторон треугольника.
Теорема косинусов гласит:
c^2 = a^2 + b^2 - 2ab*cos(α)
Где c - длина гипотенузы, a и b - длины катетов треугольника.
Для нахождения угла α нам необходимо аккуратно переписать формулу, выражая острый угол:
cos(α) = (a^2 + b^2 - c^2) / (2ab)
Теперь, зная значения длин сторон треугольника, мы можем вычислить cos(α) и затем найти острый угол α при помощи тригонометрической функции арккосинус (acos):
α = acos(cos(α))
Таким образом, при известных сторонах прямоугольного треугольника можно найти острый угол α, используя формулы теоремы косинусов и тригонометрическую функцию арккосинус.
Применение острых углов в реальной жизни
Острые углы в прямоугольном треугольнике имеют множество применений в реальной жизни. Они используются в различных областях, включая геометрию, архитектуру, инженерное дело и навигацию.
В геометрии, острые углы помогают определить форму и размеры треугольников. Они используются для вычислений и решения геометрических задач. Например, при построении графиков и построении треугольников по заданным углам и сторонам.
В архитектуре, острые углы могут использоваться при разработке планов зданий и конструкций. Они помогают определить правильный угол для стыковки стен и помогают создать прочные и устойчивые конструкции. Острые углы также могут использоваться при разбиении пространства или расположении окон и дверей.
В инженерном деле, острые углы могут быть применены при проектировании механизмов и машин. Они помогают определить углы поворота или наклона частей механизма, а также направление движения. Острые углы также используются при проектировании электронных схем и прецизионных инструментов.
В навигации, острые углы могут использоваться для определения направления движения или местоположения объекта. Например, в морской навигации острые углы используются для вычисления курса и позиции судна относительно звезд и других навигационных точек.
В целом, острые углы в прямоугольном треугольнике являются важным математическим понятием, который имеет широкое применение в различных областях. Они помогают нам понять и изучить мир вокруг нас, а также использовать этот знак для решения практических задач и проблем.



