Фигуры - один из фундаментальных объектов в математике. Они являются основным предметом изучения в геометрии и широко применяются в различных областях, включая физику, архитектуру, и даже искусство. Общие свойства фигур позволяют нам изучать их формы, размеры, отношения и многое другое.
Одним из основных принципов, лежащих в основе изучения фигур, является классификация их по свойствам. Форма - это одно из наиболее важных свойств фигуры, определяющее ее внешний вид. Фигуры могут быть геометрическими или неопределенными, симметричными или несимметричными, регулярными или нерегулярными.
Примерами таких фигур являются круг, треугольник, квадрат и прямоугольник. Круг - это геометрическая фигура, состоящая из всех точек в плоскости, равноудаленных от центра. Треугольник - фигура с тремя сторонами и тремя углами. Квадрат и прямоугольник - это фигуры с четырьмя прямыми сторонами и прямыми углами.
Формы и их свойства

В математике формы играют важную роль при изучении различных объектов. Форма представляет собой внешний облик или геометрический вид объекта. В зависимости от типа и свойств формы, у нас может быть множество разных фигур: треугольники, прямоугольники, окружности, эллипсы и много других.
Каждая форма обладает определенными свойствами, которые позволяют нам анализировать их и сравнивать между собой.
Одно из основных свойств формы - ее площадь. Площадь показывает, сколько плоскости занимает объект. Например, площадь прямоугольника равна произведению его длины на ширину.
| Форма | Площадь |
|---|---|
| Прямоугольник | Длина * Ширина |
| Круг | π * Радиус^2 |
| Треугольник | (Основание * Высота) / 2 |
Еще одно важное свойство формы - ее периметр. Периметр показывает длину границы фигуры. Например, периметр прямоугольника равен удвоенной сумме его сторон.
| Форма | Периметр |
|---|---|
| Прямоугольник | 2 * (Длина + Ширина) |
| Круг | 2 * π * Радиус |
| Треугольник | Сумма всех сторон |
Это только некоторые свойства форм. Каждая фигура имеет свои особенности и можно выделить еще множество других свойств: радиус, диаметр, высоту, ширину и т.д. Изучение этих свойств позволяет нам лучше понять и описать формы математически.
Определение и классификация фигур

Фигуры классифицируются в зависимости от различных свойств, таких как количество сторон, тип и форма этих сторон, наличие или отсутствие углов, симметрия и многое другое. В результате этой классификации, фигуры делятся на несколько основных категорий.
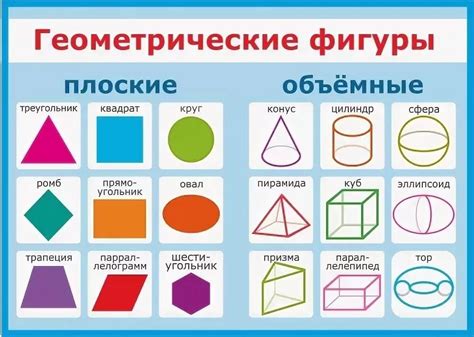
1. Геометрические фигуры в двух измерениях:
- Одномерные фигуры – линии. Примеры: отрезок, прямая, изломанная, окружность.
- Двумерные фигуры – плоские фигуры. Примеры: треугольник, квадрат, прямоугольник, ромб, трапеция, круг и многие другие.
2. Геометрические фигуры в трех измерениях:
- Трехмерные фигуры – объемные фигуры. Примеры: куб, параллелепипед, пирамида, конус, цилиндр, сфера и многие другие.
3. Фигуры с определенными свойствами:
- Регулярные фигуры – фигуры, у которых все стороны и углы равны. Примеры: правильный треугольник, квадрат, правильный пятиугольник.
- Нерегулярные фигуры – фигуры, у которых стороны и углы не равны. Примеры: прямоугольник, трапеция, неравносторонний треугольник.
- Симметричные фигуры – фигуры, у которых существует ось симметрии, разделяющая фигуру на две равные части. Примеры: квадрат, круг, ромб.
Классификация фигур позволяет упорядочить и систематизировать их, делая математическое изучение и анализ более удобными. Знание основных типов фигур и их свойств помогает строить графики, решать геометрические задачи и применять математические модели в реальных ситуациях.
Основные принципы изучения фигур
Первым принципом изучения фигур является определение их свойств. Фигуры могут иметь различные характеристики, такие как форма, размеры, углы, стороны и диагонали. Изучение этих свойств позволяет классифицировать их и понять их взаимосвязи.
Вторым принципом изучения фигур является анализ их параметров. Параметры фигур определяются их характеристиками и могут использоваться для сравнения их между собой. Например, при анализе прямоугольников можно сравнивать их длины и ширины, а при анализе треугольников - их стороны и углы.
Третьим принципом изучения фигур является классификация. Фигуры могут быть классифицированы в различные группы в зависимости от своих характеристик. Например, прямоугольники могут быть разделены на квадраты и прямоугольники общего вида в зависимости от соотношения их сторон.
Четвертым принципом изучения фигур является синтез. Синтез представляет собой процесс создания новых фигур из уже известных. Это помогает понять взаимосвязь между различными геометрическими формами и использовать их для создания новых конструкций.
Изучение основных принципов фигур помогает развивать логическое мышление и понимание математических концепций. Оно также имеет практическое применение в различных областях, таких как архитектура, инженерия, дизайн и наука.
Примеры фигур
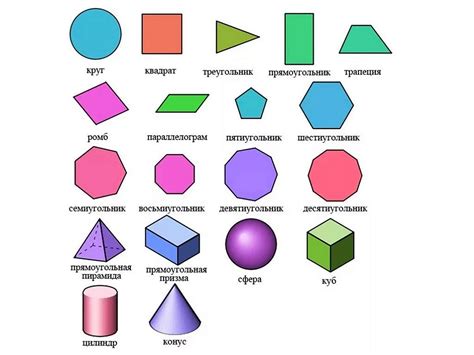
В математике существует большое разнообразие фигур, каждая из которых обладает своими уникальными свойствами. Некоторые из наиболее известных и часто встречающихся фигур включают в себя:
1. Круг - фигура, образованная всеми точками, находящимися на одном и том же расстоянии от центра. Круг обладает свойством радиуса - расстояния от центра до любой точки на границе.
2. Прямоугольник - фигура с четырьмя прямыми углами и противоположными параллельными сторонами. У прямоугольника есть две основные характеристики: длина и ширина.
3. Треугольник - фигура с тремя сторонами и тремя углами. Три основных типа треугольников включают правильный треугольник, равнобедренный треугольник и разносторонний треугольник.
4. Квадрат - особый прямоугольник, у которого все четыре стороны равны. Квадрат обладает свойствами всех прямоугольников, а также имеет углы прямого вида.
5. Куб - трехмерная фигура, у которой все шесть граней являются квадратами. Куб имеет свойства, характерные как для квадрата, так и для трехмерных фигур.
6. Окружность - особый случай круга, где все точки находятся на одном и том же расстоянии от центра, но без границы.
Это лишь некоторые примеры фигур, которые используются в математике для изучения и анализа. Каждая из этих фигур имеет свои уникальные свойства и применения в различных областях.
Прямоугольник
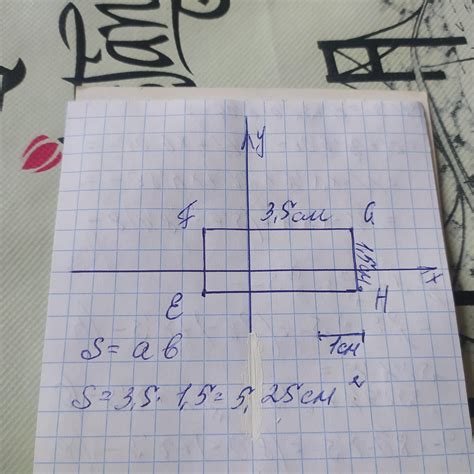
Основные свойства прямоугольника:
- Противоположные стороны прямоугольника равны в длине и параллельны друг другу.
- Противоположные углы прямоугольника равны 90 градусам.
- Диагонали прямоугольника равны по длине и пересекаются в середине.
- Площадь прямоугольника вычисляется по формуле: S = a * b, где a и b – длины сторон.
- Периметр прямоугольника вычисляется по формуле: P = 2a + 2b, где a и b – длины сторон.
Прямоугольники встречаются в различных сферах нашей жизни. Например, форма большинства окон, дверей, телевизоров, столов и других предметов бытового обихода соответствует прямоугольнику.
Примеры прямоугольников:
- Лист бумаги обычно имеет форму прямоугольника.
- Монитор компьютера имеет прямоугольную форму.
- Стандартный рабочий стол на компьютере имеет прямоугольную форму.



