Линейное программирование – это математический метод, который используется для решения задач оптимизации. Основная задача линейного программирования заключается в нахождении оптимального решения для системы линейных уравнений или неравенств, учитывая ограничения и целевую функцию.
Оптимизация решений является одним из самых важных аспектов линейного программирования. Цель состоит в том, чтобы найти наилучшее решение, удовлетворяющее всем условиям и ограничениям задачи. В основе этого метода лежит стремление максимизировать или минимизировать целевую функцию, которая отражает желаемый результат или критерий успешности.
Для достижения оптимального решения линейные программы используются в различных областях, таких как экономика, производство, логистика и многие другие. Метод линейного программирования позволяет принимать сложные решения, основываясь на математическом анализе и моделировании, а также учитывая различные ограничения и факторы, которые могут повлиять на результат.
Что такое линейное программирование?

Линейное программирование применяется в различных областях, таких как бизнес, экономика, инженерия и транспорт. Основная задача линейного программирования состоит в том, чтобы найти оптимальное значение переменных, удовлетворяющее всем условиям и минимизирующее или максимизирующее целевую функцию.
Для решения задачи линейного программирования обычно используется симплекс-метод, который основывается на поочередном улучшении решений. Симплекс-метод позволяет находить оптимальное решение путем последовательного перехода от одного базисного решения к другому, пока не будет достигнуто оптимальное значение.
Важными элементами линейного программирования являются:
- Целевая функция - это функция, которую необходимо минимизировать или максимизировать. Она выражает цель или задачу, которую нужно достичь.
- Ограничения - это условия, которые определяют допустимое множество значений переменных. Они могут быть линейными или неравенствами.
- Переменные решения - это значения, которые нужно найти, чтобы достичь оптимального решения. Они обычно обозначаются символами и являются неотрицательными.
Линейное программирование позволяет находить оптимальные решения для сложных задач, которые связаны с распределением ограниченных ресурсов, планированием производства, управлением запасами и другими. Оно предоставляет математическую основу для принятия рациональных и эффективных решений в различных областях деятельности.
Линейное программирование: определение и основные понятия

Суть линейного программирования заключается в том, чтобы найти оптимальное значение целевой функции при условии выполнения набора ограничений. Целевая функция - это выражение, которое нужно минимизировать или максимизировать, а ограничения - это условия, которые должны быть выполнены.
Основные понятия, связанные с линейным программированием:
- Решение задачи линейного программирования - это набор значений переменных, которые удовлетворяют всем ограничениям и оптимизируют целевую функцию.
- Ограничения - это условия, которые ограничивают значения переменных и влияют на возможные решения задачи.
- Целевая функция - это функционал, который оптимизируется. Он может быть как максимизирующим, так и минимизирующим.
- Однородные ограничения - это ограничения, в которых все переменные участвуют с одинаковым коэффициентом.
- Неравенства - это ограничения, в которых значения выражений должны быть больше или меньше определенного значения.
- Оптимальное решение - это решение, которое обладает наилучшим значением целевой функции при условии выполнения ограничений.
- Допустимое решение - это решение, которое удовлетворяет всем ограничениям задачи.
Линейное программирование широко применяется в экономике, производственном менеджменте, логистике и других областях, где необходимо делать оптимальные решения с ограниченными ресурсами. Оно позволяет эффективно использовать доступные ресурсы и повышать эффективность процессов.
Примеры применения линейного программирования в реальной жизни

Одной из областей, где линейное программирование находит применение, является логистика. В логистике этот метод используется для оптимизации планирования доставки грузов и маршрутов транспорта. С помощью линейного программирования можно определить оптимальный план доставки грузов, который учитывает ограничения на количество доступного транспорта, время доставки и расходы на топливо. Это позволяет снизить затраты и повысить эффективность логистических операций.
Еще одним примером применения линейного программирования является финансовое планирование. Например, банки могут использовать этот метод для оптимизации распределения активов и управления рисками. С помощью линейного программирования можно оптимально распределить финансовые ресурсы между различными инвестиционными инструментами, учитывая риски и доходность каждого из них.
Еще одной областью, где линейное программирование применяется, является производственная деятельность. Метод используется для оптимизации процессов производства, планирования производственных мощностей и управления запасами. С помощью линейного программирования можно определить оптимальное соотношение производственных ресурсов, чтобы минимизировать затраты на производство и максимизировать выпуск продукции.
Кроме того, линейное программирование находит применение в маркетинге и рекламе. Например, компании могут использовать этот метод для оптимизации распределения рекламного бюджета между различными каналами, чтобы максимизировать охват целевой аудитории и увеличить конверсию. Также линейное программирование может быть использовано для оптимизации ценовой политики и расчета оптимальных цен на товары и услуги.
Таким образом, линейное программирование является мощным инструментом, который находит широкое применение в различных областях деятельности. Оно позволяет оптимизировать решения, учитывая ограничения и цели, и способствует повышению эффективности и экономической эффективности в разных сферах жизни.
Преимущества использования линейного программирования
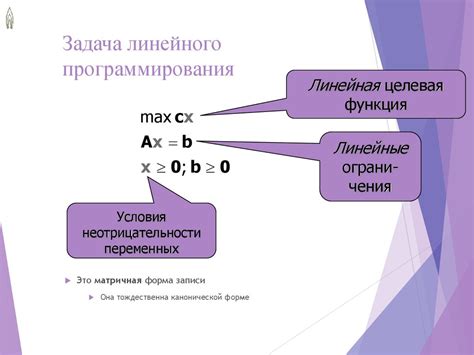
Линейное программирование представляет собой мощный инструмент для оптимизации решений и принятия эффективных решений в различных областях деятельности.
Вот несколько преимуществ использования линейного программирования:
1. Оптимальное использование ресурсов: Линейное программирование позволяет оптимально распределить ограниченные ресурсы, такие как время, деньги и материалы, для достижения максимальной выгоды или минимальных затрат. Это особенно важно в производственных и логистических системах, где правильное использование ресурсов может привести к значительным экономическим выгодам.
2. Учет сложных ограничений: Линейное программирование способно учесть различные сложные ограничения, такие как ограничения на производственные мощности, логистические ограничения и ограничения на качество продукции. Оно позволяет учесть все эти ограничения при оптимизации решений, что помогает достичь лучших результатов.
3. Решение многокритериальных задач: Линейное программирование может быть использовано для решения задач с несколькими критериями. Вместо того, чтобы оптимизировать один конкретный показатель, такой как прибыль, можно оптимизировать несколько показателей одновременно. Это особенно полезно при принятии решений в сложных системах, где необходимо учесть множество факторов.
4. Простота использования: Линейное программирование имеет относительно простую формулировку и решение. Оно может быть эффективно применено с использованием компьютерных программ, что позволяет быстро и точно найти оптимальное решение. Это делает линейное программирование доступным и удобным инструментом для различных предприятий и организаций.
В целом, линейное программирование является мощным и универсальным инструментом, который может быть применен во многих областях деятельности для достижения оптимальных результатов и улучшения эффективности решений.
Задачи, решаемые с помощью линейного программирования

С помощью линейного программирования можно решить множество задач. Одной из таких задач является задача о производстве, где требуется определить оптимальные объемы производства различных товаров с учетом ограничений на доступные ресурсы. Например, компания, производящая разные типы продуктов, может использовать линейное программирование для определения оптимального распределения ресурсов (сырья, оборудования, рабочей силы) и минимизации затрат.
Еще одной задачей, решаемой с помощью линейного программирования, является задача о распределении ресурсов. В организациях с ограниченными бюджетами такая задача актуальна. Например, университет может использовать линейное программирование для оптимальной расстановки студентов по различным курсам с учетом ограничений на количество мест и предпочтений студентов.
Также линейное программирование может быть применено для решения задач транспортировки. Например, логистическая компания может использовать его для определения оптимального маршрута доставки груза с учетом ограничений на вес, объем и доступность путей.
Задачи оптимизации решений с помощью линейного программирования также находят применение в финансовой сфере. Например, инвестиционные компании могут использовать его для определения оптимального портфеля инвестиций с учетом желаемого дохода и уровня риска. Также линейное программирование может помочь в оптимизации расписания торговых операций и управлении портфелем акций.
Таким образом, линейное программирование широко используется для решения различных задач оптимизации решений. Оно позволяет найти оптимальные решения с учетом ограничений и достигнуть максимальной эффективности в различных областях деятельности.
Как решать задачи линейного программирования

Решение задачи линейного программирования включает несколько этапов:
- Определение целевой функции. Сначала необходимо определить, какую величину требуется оптимизировать. Целевая функция может быть как максимизирующей, так и минимизирующей.
- Описания ограничений. Далее необходимо сформулировать все ограничения, которые должны быть учтены при решении задачи.
- Построение математической модели. На основе целевой функции и ограничений строится математическая модель, которая представляет собой систему линейных неравенств и уравнений.
- Поиск оптимального решения. С помощью специальных алгоритмов и методов оптимизации выполняется поиск оптимального решения задачи.
- Анализ результатов. После нахождения оптимального решения, необходимо проанализировать полученные результаты с точки зрения их практической применимости и соответствия поставленным целям.
Применение методов линейного программирования позволяет эффективно решать различные практические задачи. Они находят применение в таких областях, как экономика, финансы, производство, логистика и многих других.
Важно отметить, что решение задач линейного программирования требует высокой математической подготовки и использования специализированных программных средств.
Методы решения задач линейного программирования

Существует несколько методов решения задач линейного программирования, каждый из которых обладает своими особенностями и применяется в различных ситуациях:
1. Графический метод – основанный на построении графиков ограничений и исследовании их пересечений. Позволяет найти решение задачи с помощью графического представления.
2. Симплекс-метод – самый распространенный метод решения задач линейного программирования. Основан на систематическом переборе опорных решений и движении от одного базисного решения к другому до достижения оптимального решения.
3. Метод искусственного базиса – используется для решения задач с неравенствами и установлением начального базиса. Осуществляется путем введения дополнительных переменных и поэтапным исключением их из выражения.
4. Двойственность – метод, основанный на обращении задачи линейного программирования и изучении ее двойственной формы. Позволяет находить оценки на оптимальное решение и проводить чувствительностный анализ модели.
5. Внутренняя точка – метод, основанный на итерационном приближении решения задачи с помощью поиска внутренней точки многогранника ограничений.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного зависит от условий задачи и требуемой точности результата.
Различные подходы к решению задач линейного программирования
- Графический метод: один из самых простых способов решения задач линейного программирования, который основан на построении графика ограничений и нахождении точки пересечения линий этих ограничений. Графический метод позволяет наглядно представить и анализировать решение задачи.
- Симплекс-метод: один из самых популярных и эффективных способов решения задач линейного программирования. Он основан на применении особого алгоритма, называемого симплекс-алгоритмом, который позволяет найти оптимальное решение, перебирая различные базисные переменные и улучшая значение целевой функции на каждом шаге.
- Интериор-поинт метод: метод, использующий итерационный подход для нахождения решений задач линейного программирования. Он основывается на поиске интериорного решения, то есть решения, находящегося внутри области ограничений. Интериор-поинт метод часто применяется для решения задач с большим количеством переменных и ограничений.
Каждый из перечисленных подходов имеет свои преимущества и ограничения, поэтому выбор конкретного метода зависит от ряда факторов, таких как размер задачи, допустимое время вычислений и требуемая точность результата. Важно выбирать подход, который наиболее эффективно и точно справится с поставленной задачей.
Проблемы и ограничения линейного программирования
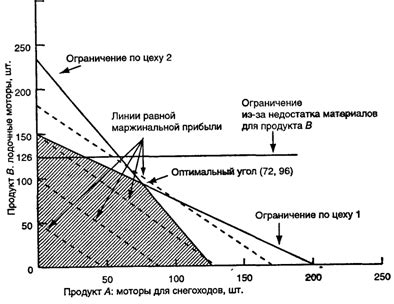
Одной из основных проблем линейного программирования является ограничение на линейные функции. Все ограничения и целевая функция должны быть заданы в виде линейных уравнений или неравенств. Это ограничивает возможности моделирования комплексных систем, которые могут иметь нелинейные зависимости или ограничения.
Кроме того, линейное программирование предполагает, что все параметры модели являются точными и известными. Однако на практике это не всегда так. Часто параметры модели подвержены неопределенности или изменяются во времени. Это может приводить к неточности и неоптимальным решениям при использовании линейного программирования.
Еще одной проблемой линейного программирования является ограничение на дискретные решения. Линейное программирование предполагает, что все переменные могут принимать любое допустимое значение в заданных интервалах. Однако в реальности некоторые переменные могут принимать только дискретные значения, что ограничивает применимость линейного программирования.
Также стоит отметить, что линейное программирование не учитывает возможные внешние факторы или ограничения, которые могут повлиять на решение. Например, изменение рыночных условий или политических решений может потребовать пересмотра оптимального решения, полученного с помощью линейного программирования.



