Основание позиционной системы счисления - это число, которое определяет количество символов, используемых для представления чисел в данной системе. В обычной десятичной системе счисления основание равно 10, так как мы используем 10 цифр для обозначения чисел (от 0 до 9).
Однако, в других позиционных системах счисления основание может быть другим. Например, в двоичной системе счисления основание равно 2, так как используются только две цифры - 0 и 1. В восьмеричной системе основание равно 8, а в шестнадцатеричной системе - 16.
Основание позиционной системы счисления определяет, какие числа могут быть представлены в данной системе и как они записываются. Например, в двоичной системе счисления с основанием 2 можно записать только числа, состоящие из цифр 0 и 1. А в восьмеричной системе счисления с основанием 8 используются цифры от 0 до 7.
Знание основания позиционной системы счисления важно при работе с различными системами счисления, а также в информатике, программировании и криптографии. Понимание основания позволяет легче понять принципы и алгоритмы работы с числами в разных системах счисления.
Что такое основание позиционной системы счисления?

Однако, позиционная система счисления может иметь и другие основания. Например, в двоичной системе счисления, основание равно 2, и для представления чисел используются только две уникальных цифры: 0 и 1. В восьмеричной системе счисления основание равно 8, а используются цифры от 0 до 7.
Уникальные символы представляют различные степени основания, которые определяют вклад каждой позиции цифры в общее значение числа. Например, в десятичной системе счисления, позиция цифры определяет, сколько раз ее значение умножается на степень 10. Это позволяет нам представлять числа различной длины и значения с помощью ограниченного набора цифр.
Основание позиционной системы счисления является важным понятием для понимания и работы с различными системами счисления. Знание основания позволяет нам производить математические операции, конвертировать числа из одной системы в другую и выполнять другие операции, связанные с числами и их представлением.
Определение и принцип работы
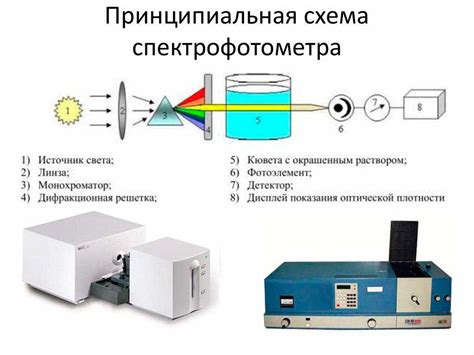
Принцип работы позиционной системы счисления заключается в том, что каждый разряд числа имеет свой вес, определяемый основанием системы. Например, в десятичной системе первый разряд считается единицами, второй - десятками, третий - сотнями и так далее. Каждый разряд умножается на соответствующий ему вес и все полученные значения суммируются для получения итогового числа.
Например, число "456" в десятичной системе можно разложить следующим образом: 4 * 100 + 5 * 10 + 6 * 1. В итоге получаем число 456.
В позиционной системе счисления все числа можно представить с помощью ограниченного набора символов, а использование весов разрядов позволяет представлять числа различных величин с помощью одних и тех же символов. Это делает позиционную систему счисления удобной и эффективной для выполнения арифметических операций и представления различных типов данных.
Примеры основания системы счисления

Существует несколько распространенных оснований системы счисления, которые используются в разных областях:
| Основание | Обозначение | Примеры |
|---|---|---|
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Двоичная | 2 | 0, 1 |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Это лишь некоторые примеры оснований системы счисления. Конкретное основание выбирается в зависимости от требуемого количества символов для представления чисел и конкретных потребностей конкретной области применения.
Преимущества и недостатки использования определенного основания

Позиционная система счисления предоставляет нам возможность представлять числа с помощью различных оснований. Каждое из оснований имеет свои преимущества и недостатки, которые стоит учитывать при выборе системы счисления.
Основание 10 является наиболее распространенным в повседневной жизни, и мы все привыкли к нему. Оно обладает простотой использования и удобством для человека, так как большинство из нас использует десятичные дроби и ведет расчеты на основе этого основания. Также основание 10 позволяет без проблем выполнять деление на наиболее часто используемые числа, такие как 2, 5 и 10.
Однако использование основания 10 имеет свои недостатки. Например, при выполнении длинных вычислений часто возникают бесконечные десятичные разложения, требующие округления. Это может привести к потере точности и дополнительным ошибкам. Также в некоторых случаях десятичные числа не могут быть точно представлены в двоичной форме, что приводит к ошибкам округления и неточности расчетов.
Основание 2 (двоичная система счисления) обладает преимуществами в компьютерах и цифровых устройствах. Использование двоичной системы позволяет упростить и ускорить операции с целыми числами, так как они сводятся к простым битовым операциям (логическое И, ИЛИ, и т.д.). Основание 2 также позволяет более точно представлять вещественные числа с фиксированной точностью, так как дробная часть может быть представлена в виде битовых дробей.
Однако основание 2 имеет свои недостатки для человека. Двоичные числа неудобны для чтения и запоминания, так как они обычно состоят из большого количества символов. Также вычисления с использованием основания 2 могут быть более сложными для человека, особенно при выполнении операций с большими числами.
Сравнение различных оснований системы счисления

Основание позиционной системы счисления определяет количество различных символов, которые используются для представления чисел. Различные основания имеют свои преимущества и ограничения, которые влияют на удобство и эффективность использования.
Основания систем счисления могут быть разных типов - двоичное (основание 2), восьмеричное (основание 8), десятичное (основание 10), шестнадцатеричное (основание 16) и другие.
Наиболее распространенное основание системы счисления - десятичное. Оно широко используется в повседневной жизни и наиболее удобно для людей, поскольку мы имеем десять различных цифр и можем легко производить арифметические операции. Однако десятичная система требует большего количества символов для представления чисел больше десяти.
Двоичная система счисления, основанная на двух символах (0 и 1), часто используется в компьютерах и электронике. Эта система обеспечивает простую и надежную работу со схемами и логическими операциями, но требует большего количества символов для представления чисел.
Восьмеричная система счисления использует восемь различных цифр и облегчает работу с большими числами в сравнении с двоичной системой. Она часто используется в программировании и в области данных.
Шестнадцатеричная система счисления имеет основание 16 и использует цифры от 0 до 9 и буквы от A до F для представления чисел. Она является удобной для работы с большими числами и часто используется в программировании, особенно для представления цветов и адресации памяти.
Все эти основания системы счисления имеют свои уникальные особенности и применения в различных областях. Выбор основания зависит от конкретных потребностей и требований системы счисления.
Применение и распространение позиционной системы счисления
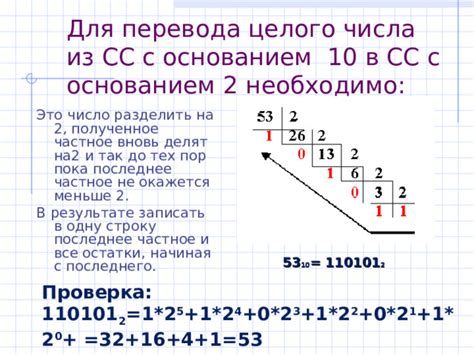
Позиционная система счисления, основанная на определенном основании, имеет широкое применение в различных областях науки, техники и повседневной жизни.
Одним из основных применений позиционной системы счисления является использование ее в компьютерах и других электронных устройствах. В этих системах информация обрабатывается и хранится в виде двоичных чисел, которые являются самой распространенной формой позиционной системы счисления. Бинарные числа, состоящие из цифр 0 и 1, позволяют компьютерам эффективно обрабатывать и передавать информацию.
Позиционная система счисления также применяется в математике для решения различных задач. Она позволяет удобно записывать и анализировать числа и их свойства. В основе многих алгоритмов и методов науки лежат понятия и операции, основанные на позиционной системе счисления.
В повседневной жизни мы часто используем десятичную систему счисления, которая также является позиционной. Она позволяет легко и точно представлять и работать с числами, используя десять цифр от 0 до 9. Благодаря этому мы можем считать, покупать товары, рассчитывать расходы и доходы, а также проводить различные другие операции, связанные с числами.
Позиционная система счисления широко распространена и применяется не только в наше время, но и на протяжении всей истории человечества. Другие позиционные системы счисления, такие как восьмеричная и шестнадцатеричная, также используются в различных областях, включая программирование, электронику, математику и компьютерные науки.
| Система счисления | Основание |
|---|---|
| Двоичная | 2 |
| Восьмеричная | 8 |
| Десятичная | 10 |
| Шестнадцатеричная | 16 |



