Симметрия – одно из основных понятий в геометрии. В ее основе лежит идея равенства двух или более геометрических объектов относительно некоторого элемента.
Существует несколько видов симметрии, одним из которых является осевая симметрия. Она описывает случай, когда фигура остается неизменной при повороте на 180 градусов вокруг прямой оси. Осевая симметрия можно наблюдать, например, у буквы "А", у круга или у любого другого объекта, который симметричен относительно своей центральной оси.
Центральная симметрия – другой вид симметрии, при котором объект остается неизменным при повороте на определенный угол вокруг заданной точки. Эта точка называется центром симметрии. Примером центральной симметрии может служить знак бесконечности или отражение растения в воде.
Осевая и центральная симметрия являются важными понятиями в геометрии и находят применение в различных областях науки и искусства. Они помогают нам лучше понять и описать структуру и форму объектов, а также придают им гармоничность и эстетическую привлекательность.
О новых определениях

Осевая симметрия, также известная как зеркальная симметрия, представляет собой свойство фигуры быть симметричной относительно оси. Возьмем, например, отрезок, представляющий линию симметрии. Если мы сложим этот отрезок вдоль оси, то получим две половинки, которые будут идентичными и совпадать друг с другом.
Центральная симметрия, с другой стороны, является свойством фигуры быть симметричной относительно центра. В этом случае, любая точка на фигуре имеет парную точку, которая находится на равном расстоянии от центра, но в противоположном направлении. Такая симметрия часто наблюдается в природе, например, в строении цветков.
Уникальность осевой и центральной симметрии заключается в их простоте и ясности. Они являются важными инструментами для анализа и понимания геометрических фигур, а также для создания гармоничных и симметричных композиций в искусстве и дизайне.
Особенности осевой симметрии
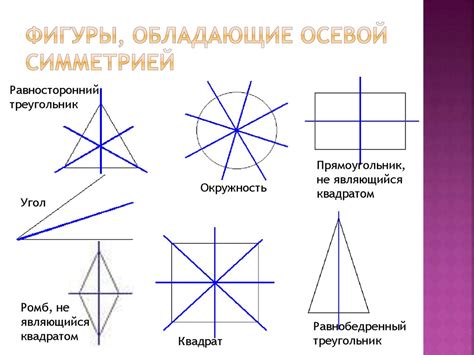
Имеются несколько основных особенностей, которые характеризуют осевую симметрию:
- Осевая симметрия имеет две стороны: левую и правую. Объект или фигура, обладающие осевой симметрией, будут выглядеть одинаково, если их разделить пополам вдоль оси симметрии и сложить получившиеся половинки.
- Ось симметрии является воображаемой линией. Она может быть вертикальной, горизонтальной или диагональной, в зависимости от объекта или фигуры.
- Фигуры с осевой симметрией могут быть простыми или сложными. Некоторые примеры объектов с осевой симметрией включают: окружности, прямоугольники, треугольники и многогранники.
- Осевая симметрия является важным понятием в геометрии и искусстве. Многие архитектурные постройки и произведения искусства, такие как садовые фигуры и живописные картины, могут включать элементы с осевой симметрией, чтобы создать гармоничный и сбалансированный образ.
- Осевая симметрия может быть использована в различных задачах и вычислениях. Она помогает упростить геометрические конструкции и решать уравнения.
Осевая симметрия является важным понятием в математике и присутствует в различных аспектах нашей жизни. Понимание основных особенностей осевой симметрии поможет вам анализировать и узнавать ее в различных объектах и фигурах.
Примеры объектов с осевой симметрией
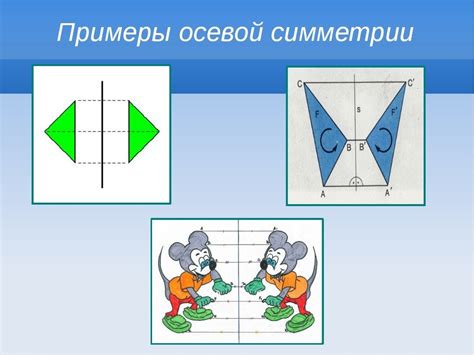
Примерами объектов с осевой симметрией могут служить:
Человек: Человеческое тело обладает осевой симметрией, причем осевая плоскость проходит через центр тела от вершины головы до нижней части тела. В результате, левая и правая стороны тела симметричны друг другу.
Архитектурные сооружения: Множество зданий и памятников архитектуры имеют осевую симметрию. Например, многие дворцы, соборы и сады строятся с использованием осевой симметрии в своем дизайне, чтобы создать гармоничный и эстетически приятный образ.
Растения: Многие растения могут обладать осевой симметрией. Например, цветы, такие как тюльпаны, лилии и розы, имеют симметричную форму относительно своей центральной оси, что делает их красивыми и гармоничными.
Геометрические фигуры: Некоторые геометрические фигуры обладают осевой симметрией. Например, прямоугольник, квадрат и круг имеют осевую симметрию, потому что их формы не изменяются при повороте вокруг своей оси на 180 градусов.
Животные: Некоторые животные, такие как бабочки и раки, обладают осевой симметрией. Они имеют симметричную форму тела относительно своей оси, что помогает им выполнять различные движения и функции.
Это лишь несколько примеров объектов с осевой симметрией. Этот принцип симметрии широко используется во многих областях и оказывает важное влияние на нашу восприятие и визуальный опыт.
Особенности центральной симметрии
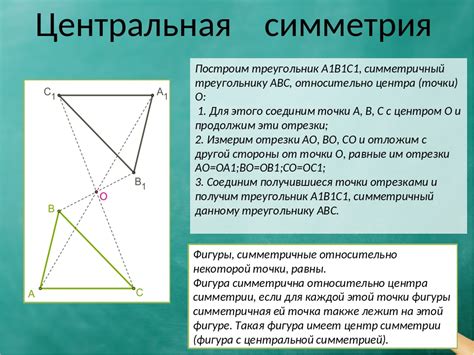
Существует несколько особенностей, которые характеризуют центральную симметрию:
| 1. | Любая прямая, проходящая через центр симметрии, является осью симметрии. Это означает, что если мы проведем прямую линию от центра симметрии до любой точки на объекте, то расстояние от этой точки до центра будет равно расстоянию от симметричной точки до центра симметрии. |
| 2. | В центральной симметрии длина отрезка, соединяющего точку с её симметричной относительно центра симметрии, остается неизменной. Это свойство называется сохранением расстояния. |
| 3. | Если объект имеет центр симметрии, то он сохраняет все свои основные характеристики при отражении. Таким образом, если у объекта есть определенные длины сторон, углы и пропорции, то они останутся такими же после отображения. |
Центральная симметрия широко применяется в геометрии, искусстве и архитектуре. Она позволяет создавать изящные и симметричные узоры, структуры и композиции.
Примеры объектов с центральной симметрией
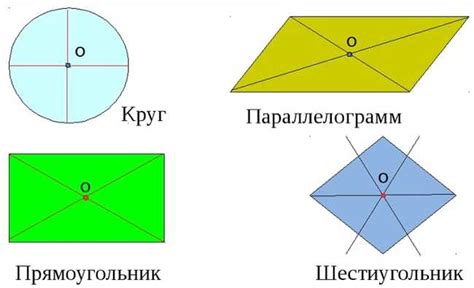
Примеры объектов с центральной симметрией:
- Круг: любая точка внутри круга является его центром симметрии. Если провести линию от центра круга к любой точке на его границе, эта линия будет радиусом, и объект будет зеркально отражаться относительно этой линии.
- Шестиугольник: шестиугольник, имеющий одну из своих сторон как ось симметрии, будет иметь центр симметрии в точке пересечения всех его диагоналей.
- Звезда: многие звезды имеют центральную симметрию. Линия, проведенная от центра звезды через ее конечные точки, будет служить осью симметрии.
- Квадрат: если провести линию от центра квадрата к его противоположной вершине, эта линия будет служить осью симметрии, и объект будет зеркально отражаться относительно этой линии.
Центральная симметрия имеет много применений в различных областях, включая геометрию, дизайн и искусство. Понимание этого понятия может помочь в создании симметричных композиций и улучшить эстетическое восприятие объектов.
Сравнение осевой и центральной симметрии
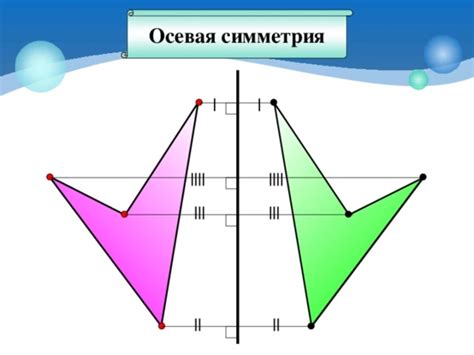
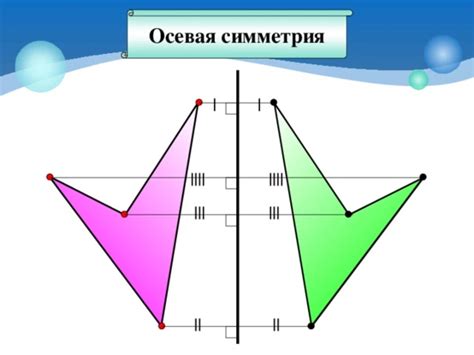
Осевая симметрия, также известная как симметрия относительно оси, проявляется в том, что фигура может быть разделена на две симметричные половины одной и той же формы и размера. Если фигура выглядит одинаково, когда ее поворачивают на 180 градусов вокруг оси симметрии, то это означает, что она обладает осевой симметрией. Примерами фигур с осевой симметрией являются прямоугольник, квадрат и круг.
С другой стороны, центральная симметрия отражает отношения между точками относительно центральной точки. Центрально-симметричная фигура может быть разделена на две половины, которые симметрично расположены по отношению к центральной точке. В таком случае, если фигура выглядит одинаково при отражении ее вокруг этой центральной точки, она обладает центральной симметрией. Примерами фигур с центральной симметрией являются круг или равносторонний треугольник.
Хотя и осевая и центральная симметрия обнаруживают отражение или поворот формы, их различия заключаются в отношении симметрии. Осевая симметрия не требует наличия центральной точки, в то время как центральная симметрия требует наличия центральной точки относительно которой происходит отражение фигуры.
Практическое применение осевой и центральной симметрии
Дизайн и искусство
Осевая и центральная симметрия часто используются в дизайне и искусстве для создания гармоничных и сбалансированных композиций. Симметричные элементы в планировании интерьеров, архитектуре и живописи могут создавать ощущение гармонии и равновесия.
Проектирование и инженерия
Осевая и центральная симметрия играют важную роль в проектировании различных объектов. Например, при проектировании автомобилей или самолетов, симметричное расположение крыльев и других элементов помогает улучшить аэродинамические характеристики и обеспечить баланс и стабильность во время движения.
Биология и медицина
Осевая и центральная симметрия также широко распространены в биологии и медицине. Симметрия часто встречается в организации тела животных и человека. Например, у большинства животных есть осевая симметрия, благодаря которой они могут двигаться с координацией и эффективностью. Кроме того, многие медицинские исследования и операции, такие как операции на сердце или на суставах, требуют учета симметричной структуры органов и тканей.
Кристаллография и химия
Осевая и центральная симметрия играют важную роль в кристаллографии и химии. Многие кристаллические структуры обладают симметрией, которая помогает определить их свойства и состав. Это позволяет ученым изучать структуру веществ и разрабатывать новые материалы с желаемыми свойствами.



