Определенный интеграл функции f x — понятие, свойства и применение

Определенный интеграл функции f(x) – это одно из важнейших понятий математического анализа. Он позволяет вычислить площадь под графиком функции f(x) на заданном интервале [a, b].

Интеграл является обратным оператором к процессу дифференцирования, а его введение через пределы суммы является одной из основных причин успеха математического анализа. Определенный интеграл широко применяется в физике, экономике, инженерии и других областях науки, а также в решении различных задач повседневной жизни.

Для нахождения определенного интеграла функции f(x) на интервале [a, b] используется специальный символ, называемый знаком интеграла. Этот символ представляет собой стилизованную букву "S" и пишется между верхним и нижним пределами интегрирования: ∫_a^b f(x)dx.

Определенный интеграл функции fx: основные понятия

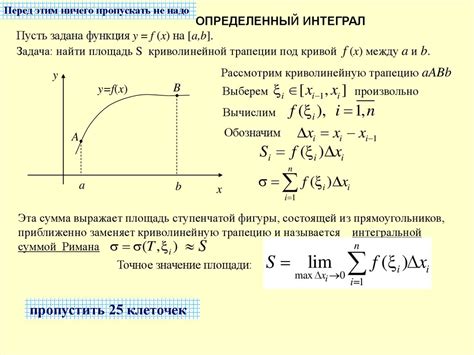
Определенный интеграл функции fx обозначается символом ∫ (интеграл) и имеет следующий вид:

∫[a, b] f(x)dx

Здесь a и b - это границы интервала, на котором будет производиться вычисление интеграла, f(x) - подинтегральная функция (интеграл от которой мы вычисляем), а dx - дифференциальный элемент. Границы a и b задают интервал интегрирования, а f(x) определяет форму графика функции.

Чтобы вычислить определенный интеграл функции fx, необходимо использовать различные методы интегрирования, такие как метод прямоугольников, метод трапеций, метод Симпсона и другие. Эти методы позволяют приближенно решать задачу и получать более точные результаты с учетом особенностей функции, формы графика и точности требуемого решения.

Определенный интеграл функции fx имеет несколько свойств и особенностей:

• Интеграл линейной функции суммируется по границам:
  ∫[a, b] (k*f(x) + m*g(x)) dx = k*∫[a, b] f(x) dx + m*∫[a, b] g(x) dx
• Интеграл функции симметричен относительно оси ординат:
  ∫[-a, a] f(x) dx = 2*∫[0, a] f(x) dx
• Интеграл функции не зависит от точки начала интегрирования:
  ∫[a, b] f(x) dx = -∫[b, a] f(x) dx

Определенный интеграл функции fx находит применение в различных областях науки, техники, экономики и других дисциплинах. Он используется для решения задач дифференциального и интегрального исчисления, нахождения площадей графиков функций, определения физических величин, моделирования процессов и многих других задач.

Начало пути в интегральном исчислении

Определенный интеграл функции f(x) - это один из двух типов интегралов, которые определяются в интегральном исчислении. Он может быть рассмотрен как пределосновной теоремы и состоит в нахождении площади под графиком функции f(x) на заданном интервале [a, b].

В математической записи определенный интеграл функции f(x) обозначается следующим образом:

∫[a, b] f(x) dx,

где [a, b] - это интервал интегрирования, f(x) - интегрируемая функция, а dx - символ дифференциала.

Интегральное исчисление предоставляет нам методы вычисления определенных интегралов, в том числе метод Ньютона-Лейбница, метод замены переменной, метод интегрирования по частям и многие другие. Эти методы позволяют выполнить интегрирование функций различного вида и сложности.

Определенный интеграл функции f(x) является одним из основных понятий интегрального исчисления. Понимание его сути и методов вычисления является важной составляющей пути к владению этой дисциплиной, позволяющей решать разнообразные математические задачи.

Что представляет собой функция fx?

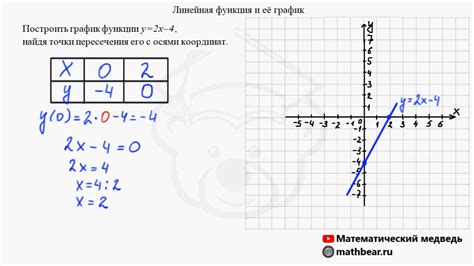
Функция f(x) представляет собой математическую операцию, которая связывает каждое значение x из определенного домена соответствующим значением y в области значений. Она описывает зависимость между двумя переменными и может быть задана в виде аналитической формулы, графика или таблицы значений.

Функции могут иметь различные формы и свойства. Они могут быть линейными, квадратичными, показательными, логарифмическими и т. д. Каждая функция имеет свои уникальные свойства, которые определяют ее поведение и характеристики.

Примеры функций включают в себя:

1. Линейную функцию: f(x) = ax + b, где a и b - постоянные значения.
2. Квадратичную функцию: f(x) = ax^2 + bx + c, где a, b и c - постоянные значения.
3. Показательную функцию: f(x) = a^x, где a - постоянная и x - переменная.

Функции используются в различных областях, включая физику, экономику, инженерию, статистику и компьютерные науки. Они позволяют моделировать и анализировать различные явления и процессы, а также предсказывать значения в заданных условиях.

Что такое интеграл?

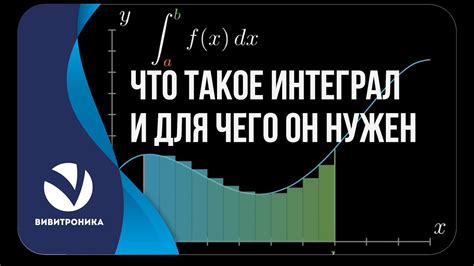
Определенный интеграл функции f(x) на отрезке [a, b] обозначается следующим образом:

∫_a^b f(x) dx

Здесь функция f(x) – это подынтегральная функция, а a и b – это начальная и конечная точки интегрирования соответственно. Знак ∫ представляет собой символ интеграла, а dx означает дифференциал переменной x, по которой берется интеграл.

Результатом вычисления определенного интеграла является число, которое описывает площадь под графиком функции на заданном отрезке.

Основные свойства определенного интеграла

Аддитивность: Если функция f(x) непрерывна на интервалах [a, b] и [b, c], то определенный интеграл от a до c можно разбить на два интеграла от a до b и от b до c. Это свойство позволяет упростить вычисления и расчеты, разбивая сложные задачи на более мелкие.

Монотонность: Если функции f(x) и g(x) непрерывны на интервале [a, b] и f(x) ≤ g(x) для всех x на этом интервале, то определенный интеграл от a до b от f(x) будет меньше или равен определенному интегралу от a до b от g(x). Это позволяет сравнивать интегралы разных функций и использовать их свойства для доказательства различных математических утверждений.

Линейность: Определенный интеграл от линейной комбинации функций равен линейной комбинации определенных интегралов от этих функций. Другими словами, интеграл от суммы двух функций равен сумме интегралов от каждой функции по отдельности. Это свойство позволяет легко вычислять интегралы от сложных функций, разбивая их на более простые составляющие.

Изменение пределов интегрирования: Определенный интеграл не зависит от конкретных значений пределов интегрирования, а только от интервала между ними. Можно изменять начальный и конечный пределы интегрирования без изменения значения интеграла. Это свойство позволяет упростить вычисления, особенно при наличии сложной функции или нестандартного интервала.

Интеграл от постоянной функции: Если функция f(x) является постоянной на интервале [a, b], то определенный интеграл от f(x) будет равен произведению значения функции на длину интервала: ∫[a, b] f(x) dx = f(x) * (b - a). Это свойство позволяет более простое вычисление интеграла в случае постоянной функции.

Эти основные свойства определенного интеграла позволяют применять его в различных областях математики и науки. Знание этих свойств позволяет выполнять более сложные вычисления и использовать интегралы для исследования различных математических моделей и задач.

Примеры вычисления определенного интеграла

Вычисление определенного интеграла может быть достаточно сложной задачей, но с помощью основных методов интегрирования можно найти точное значение интеграла. Вот несколько примеров вычисления определенного интеграла:

1. Пример 1: Вычисление определенного интеграла функции f(x) = x^2 на отрезке [0, 2]

Для вычисления определенного интеграла этой функции, мы можем использовать формулу:

∫₀² x^2 dx = [x^3 / 3]|₀²

Подставим пределы интегрирования в эту формулу:

[2^3 / 3] - [0^3 / 3] = 8 / 3 - 0 = 8 / 3

2. Пример 2: Вычисление определенного интеграла функции f(x) = cos(x) на отрезке [0, π]

Для вычисления определенного интеграла этой функции, мы можем использовать формулу:

∫₀^π cos(x) dx = [sin(x)]|₀^π

Подставим пределы интегрирования в эту формулу:

sin(π) - sin(0) = 0 - 0 = 0

3. Пример 3: Вычисление определенного интеграла функции f(x) = e^x на отрезке [0, 1]

Для вычисления определенного интеграла этой функции, мы можем использовать формулу:

∫₀¹ e^x dx = [e^x]|₀¹

Подставим пределы интегрирования в эту формулу:

e^1 - e^0 = e - 1

Таким образом, вычисление определенного интеграла требует знания основных методов интегрирования и точного подсчета значения функции в заданных пределах интегрирования.

Теорема о среднем значении для определенного интеграла

Формально, если функция f(x) непрерывна на отрезке [a, b], то существует такая точка c внутри этого отрезка, что интеграл от функции f(x) на отрезке [a, b] равен f(c) умноженному на длину отрезка (b - a). Математически это можно записать следующим образом:

∫_a^b f(x)dx = f(c) * (b - a)

Геометрически теорему о среднем значении можно понять так: существует такая точка c на оси абсцисс, что площадь под графиком функции f(x) на отрезке [a, b] равна площади прямоугольника со сторонами f(c) и (b - a).

Теорема о среднем значении для определенного интеграла имеет важное практическое применение во многих областях, связанных с анализом функций. Она позволяет переходить от интеграла к значению функции в некоторой точке, что упрощает решение различных задач.

Геометрическая интерпретация определенного интеграла

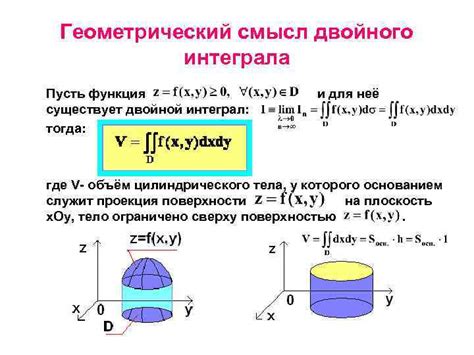
Геометрическая интерпретация определенного интеграла связана с понятием площади под графиком функции f(x) на заданном интервале [a, b]. Определенный интеграл f(x) на этом интервале представляет собой площадь фигуры, ограниченной графиком функции, осью x и вертикальными линиями x=a и x=b.

Если график функции f(x) положителен на интервале [a, b], то определенный интеграл соответствует площади, заключенной между графиком функции и осью x. Если f(x) отрицателен на интервале [a, b], то определенный интеграл будет равен отрицательной площади. Поэтому, модуль определенного интеграла в этом случае представляет собой площадь, которую отображает абсолютное значение функции f(x) на заданном интервале.

Геометрическая интерпретация определенного интеграла расширяется и на многомерный случай, когда рассматривается двойной или тройной интеграл. В этом случае на плоскости или в пространстве определенный интеграл соответствует объему фигуры, которой ограничивает функция f(x, y) или f(x, y, z) в соответствующих координатных осях.

Главный принцип геометрической интерпретации определенного интеграла заключается в том, что он позволяет использовать интеграл для нахождения площадей, объемов и других геометрических характеристик фигур, которые описываются с помощью функций. Таким образом, определенный интеграл функции f(x) представляет собой мощный инструмент для решения задач в геометрии и других областях науки и техники.

Первообразная функции и определенный интеграл

Однако, чтобы вычислить определенный интеграл, необходимо знать антипроизводную или первообразную функции F(x). Первообразная функции F(x) - это функция, производная которой равна исходной функции f(x).

Другими словами, если F'(x) = f(x), то функция F(x) является первообразной функции f(x). Знание первообразной функции позволяет найти определенный интеграл функции f(x) на заданном интервале.

Выразив определенный интеграл через первообразную функции, получаем следующую формулу:

В данной формуле, символ ∫ представляет интеграл, f(x) - исходная функция, F(x) - ее первообразная, a и b - конечные точки интервала.

Итак, для вычисления определенного интеграла функции f(x) на определенном интервале нужно:

1. Найти первообразную функцию F(x) функции f(x).
2. Подставить значения верхнего и нижнего предела интервала в первообразную функцию.
3. Вычислить разность полученных значений.

Таким образом, понимание понятия первообразной функции и связи ее с определенным интегралом помогает в решении множества задач по математическому анализу и применению его в различных областях науки и техники.

Применение определенного интеграла в реальной жизни

• Физика: Определенный интеграл используется в физике для решения задач, связанных с вычислением площади под графиками функций, определения расстояния пройденного телом по заданной траектории, вычисления работы, потока, момента и других физических величин.
• Экономика: В экономических и финансовых моделях определенный интеграл применяется для вычисления различных показателей, таких как прибыль, доходы, инфляция, инвестиции и другие экономические показатели.
• Инженерия: В различных областях инженерии, таких как механика, электротехника и строительство, определенный интеграл используется для анализа и моделирования систем, вычисления площадей и объемов, а также для определения сил, моментов и других физических параметров.
• Медицина: В медицине определенный интеграл применяется для моделирования и анализа физиологических процессов, вычисления площади под графиками, определения объемов физиологических жидкостей и других медицинских показателей.

Таким образом, определенный интеграл является мощным инструментом для решения различных задач в науке, технике и многих других областях деятельности человека.