Метрология является наукой, которая изучает физические величины и разрабатывает методы их измерения. Физические величины играют огромную роль в нашей жизни, определяя многие аспекты нашего повседневного существования. Они необходимы для описания и объяснения физических процессов и явлений, а также для установления единого и точного языка коммуникации между учеными, инженерами и производителями.
В метрологии понятие физической величины является основополагающим. Оно описывает какие-либо измеримые свойства объектов или процессов в природе. Физические величины могут быть различными: масса, длина, время, температура, сила, энергия и многое другое. Измерение физических величин позволяет оценить их значения с определенной точностью и сравнивать результаты измерений.
Значение физической величины в метрологии играет ключевую роль. Оно определяется как числовая величина, полученная в результате измерений, и сопровождается единицей измерения. Единицы измерения служат для стандартизации физических величин и обеспечивают их взаимосвязь и сопоставимость. К примеру, для измерения длины используется единица измерения - метр.
Роль физических величин в метрологии
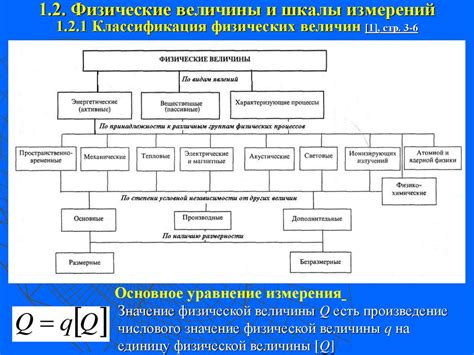
Физические величины представляют собой свойства объектов и явлений, которые могут быть измерены. Примерами физических величин могут служить масса, длина, время, энергия и температура.
В метрологии каждая физическая величина имеет свою особенность и специализацию. Например, длина измеряется в метрах, масса - в килограммах, а время - в секундах. Эти стандартные единицы измерения позволяют проводить сравнение и оценку результатов измерений.
Основная задача метрологии - обеспечение точности и единообразия измерений. Физические величины играют важную роль в достижении этой цели. Они являются основой для определения стандартов, разработки научных методов и приборов измерения, а также проведения испытаний и аттестации.
Без физических величин метрология не сможет функционировать. Они обеспечивают единообразность и точность измерений, что в свою очередь влияет на различные области человеческой деятельности, такие как наука, промышленность и торговля.
Итак, физические величины играют неотъемлемую и важную роль в метрологии. Они являются основой для создания стандартов и методов измерения, а также для проведения испытаний и аттестации. Без них невозможно достичь точности и единообразия измерений, что делает их незаменимыми в метрологической практике.
Значение точности измерений для физических величин
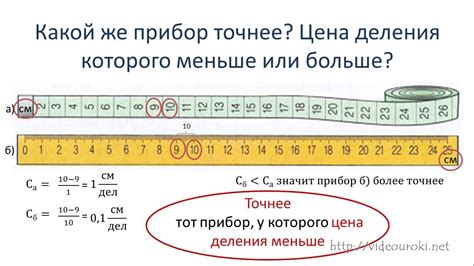
Для минимизации ошибок и повышения точности измерений метрологи используют различные методы и инструменты. Одним из основных способов повышения точности измерений является калибровка и регулярная поверка измерительных приборов. Калибровка позволяет определить погрешность измерительного прибора и скорректировать его показания. Регулярная поверка позволяет убедиться в сохранении точности измерений в течение определенного времени.
Точность измерений имеет огромное значение во многих областях науки и техники. Например, в медицине точные измерения помогают определить диагноз, назначить правильное лечение и контролировать его эффективность. В инженерии точные измерения позволяют создавать надежные и безопасные конструкции, а в производстве – контролировать качество продукции. Точные измерения также важны в научных исследованиях, где результаты эксперимента должны быть объективными и достоверными.
Для обеспечения высокой точности измерений необходимо учитывать множество факторов, таких как стабильность условий измерений, качество и калибровка измерительных приборов, квалификация исполнителя измерений и т.д. Также следует учитывать погрешности, которые могут возникать при измерении физической величины.
Погрешности измерений – это отклонения результатов измерений от реального значения физической величины. Они могут возникать из-за различных причин, таких как систематические и случайные ошибки. Систематические ошибки связаны с неправильным выбором методики измерений, некалиброванными приборами или неисправной аппаратурой. Случайные ошибки связаны с факторами, которые невозможно полностью контролировать, такими как колебания окружающей среды или несовершенство измерительных приборов.
Важность единиц измерения в метрологии
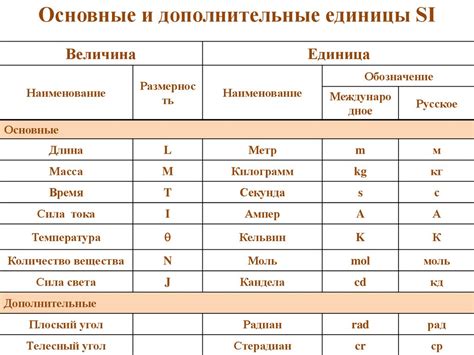
В метрологии единицы измерения играют ключевую роль, так как они позволяют стандартизировать и однозначно описывать физические величины. Единицы измерения необходимы для установления точных и надежных методов измерений, а также для обеспечения сопоставимости результатов между разными лабораториями и странами.
Единицы измерения обеспечивают ясность и точность в обмене информацией о физических величинах. Без их использования было бы очень сложно определить величину объектов или происходящих процессов. Они позволяют проводить измерения с высокой точностью и сравнивать результаты между собой.
Стандартизация единиц измерения также является неотъемлемой частью образования и науки. Без единиц измерения невозможно было бы создавать и развивать новые технологии, проводить исследования и передавать знания. Благодаря единицам измерения студенты, ученые и инженеры могут обмениваться информацией и сотрудничать в своих областях.
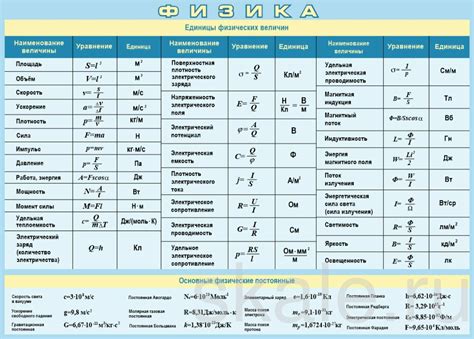
| Примеры важных единиц измерения в метрологии | Область применения |
|---|---|
| Метр (м) | Длина и расстояние |
| Килограмм (кг) | Масса и вес |
| Секунда (с) | Время |
| Ампер (А) | Электрический ток |
| Кельвин (К) | Температура |
Единицы измерения в метрологии также позволяют обеспечить безопасность и защиту потребителей. Правильные и точные измерения необходимы для контроля качества продукции, проверки соответствия стандартам и защиты от подделок. Например, стандартизированные единицы измерения позволяют проверять и контролировать массу продуктов в продовольственной и фармацевтической промышленности.
Таким образом, единицы измерения играют центральную роль в метрологии, обеспечивая точность, сопоставимость и надежность физических измерений. Без них было бы невозможно проводить научные исследования, создавать новые технологии и обеспечивать безопасность потребителей.
Функции физических величин в измерительных системах
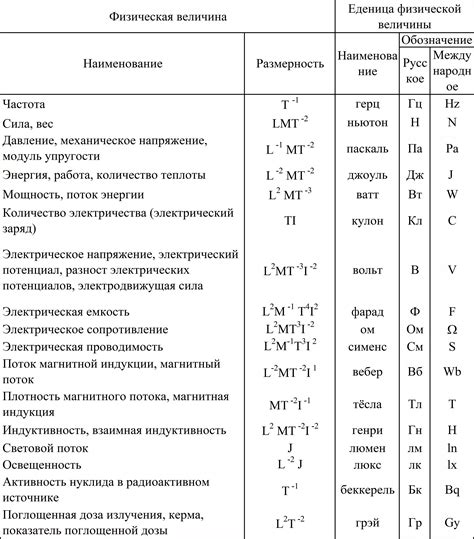
Физические величины играют важную роль в измерительных системах. Они позволяют описывать и измерять различные свойства объектов и явлений, а также устанавливать взаимосвязи между ними. Функции физических величин в измерительных системах можно разделить на несколько типов.
Первая функция физических величин - обеспечение единообразия измерений. Физические величины являются основным инструментом для сравнения и описания различных объектов и процессов. Благодаря единообразию и унификации измерений, мы можем гарантировать точность и достоверность результатов.
Вторая функция физических величин - обеспечение основы для математического описания явлений. Измеряемые физические величины позволяют устанавливать математические зависимости и уравнения, которые позволяют более глубоко изучать и понимать физические процессы.
Третья функция физических величин - обеспечение основы для создания стандартов. Физические величины используются для создания единиц измерения и международных стандартов, которые позволяют согласовывать и сравнивать результаты измерений в разных лабораториях и странах.
Четвертая функция физических величин - обеспечение контроля и управления процессами. Измерение физических величин позволяет контролировать и управлять различными процессами, например, в промышленности, науке и медицине. Они дают возможность контролировать качество продукции, мониторить состояние оборудования и проводить диагностику и лечение различных заболеваний.
Таким образом, функции физических величин в измерительных системах очень разнообразны и важны. Они позволяют нам получать точные и достоверные результаты измерений, а также разрабатывать новые технологии и достигать прогресса в различных сферах деятельности.
Влияние физических величин на результаты экспериментов

В метрологии, физические величины играют важную роль в определении и измерении различных параметров и свойств объектов. Результаты экспериментов, проведенных в рамках испытаний или исследований, напрямую зависят от точности и надежности измерений.
Физические величины могут влиять на результаты экспериментов различными способами. Во-первых, они могут повлиять на точность измерений. Если физическая величина имеет большую погрешность или неустранимую систематическую ошибку, то результаты эксперимента будут неправильными и недостоверными.
Во-вторых, физические величины могут влиять на статистическую значимость результатов. Например, если рассматривается взаимосвязь между двумя физическими величинами, то ошибки и неопределенности в измерениях одной из величин могут привести к неверной интерпретации статистической зависимости.
Наконец, физические величины могут влиять на применимость и область применения полученных результатов. Некоторые физические величины могут иметь ограничения или особенности, которые нужно учитывать при интерпретации и использовании полученных данных.
Итак, при проведении экспериментов необходимо учитывать влияние физических величин на результаты и стремиться к их максимальной точности, чтобы получить достоверные и надежные данные.
Методы обработки данных для физических величин

Один из основных методов обработки данных – математическая обработка. Она включает в себя различные операции, такие как суммирование, усреднение, экстраполяция, интерполяция и преобразование единиц измерения. Математическая обработка данных позволяет вычислить средние значения, доверительные интервалы и стандартные погрешности.
Статистическая обработка данных также широко используется в метрологии. Этот метод включает в себя анализ распределения измерений, построение графиков, определение характеристик совокупности измерений (например, среднего и дисперсии) и оценку погрешностей на основе статистических методов.
В современной метрологии широко применяются также компьютерные методы обработки данных. С использованием специализированных программ и алгоритмов возможно автоматическое выполнение сложных расчетов, построение графиков, моделирование и анализ данных. Компьютерные методы обработки данных значительно повышают эффективность и точность результатов измерений.
Важно отметить, что при обработке данных для физических величин необходимо учитывать не только точность самого измерения, но и учитывать систематические и случайные погрешности. Все методы обработки данных должны соответствовать международным стандартам и рекомендациям и быть применимыми для различных видов измерений.
Роль физических величин в стандартизации
Одна из главных задач стандартизации – обеспечение единообразия и сопоставимости измерений. Физические величины позволяют создавать системы измерений, которые обеспечивают точность, надежность и сопоставимость результатов. Например, величина времени играет важную роль во многих отраслях, и ее правильное измерение требует стандартных методов и единиц измерения.
Физические величины также помогают обеспечить безопасность и качество продукции и услуг. Они определяют требования к характеристикам и параметрам продуктов и процессов, определяют диапазоны приемлемых значений и устанавливают методы и средства для осуществления контроля и испытаний.
Кроме того, физические величины часто служат основой для разработки методов измерений и испытаний. Они позволяют установить основные принципы и процедуры, определить способы и технику измерений, а также подтвердить соответствие продукции и процессов установленным требованиям.
Таким образом, физические величины играют неотъемлемую роль в стандартизации, обеспечивая единообразие, точность, безопасность и качество в различных отраслях промышленности и науки.
Взаимосвязь физических величин в метрологии

Физические величины в метрологии обладают взаимосвязью, которая играет ключевую роль при измерениях и определении их точности. Знание связей между физическими величинами позволяет разрабатывать методы измерений, устанавливать сравнительные характеристики и определять неопределенность.
Одним из понятий, отражающих взаимосвязь физических величин, является размерность. Размерность определяет способ, с помощью которого физическая величина может быть измерена и выражена в различных единицах. Например, для измерения длины используется размерность метра, для измерения времени – секунда, для измерения массы – килограмм и так далее.
Также важное значение имеет понятие размерностного анализа. Размерностный анализ позволяет определить зависимость между различными физическими величинами и подтвердить соответствие уравнений и формул законам природы. Он выявляет прямую или обратную пропорциональность между величинами и помогает понять, как изменение одной из величин влияет на другую.
Есть также понятие погрешности, которое тесно связано с точностью и позволяет определить разброс результатов измерений. Погрешность может быть случайной или систематической. Случайная погрешность связана с непредсказуемыми факторами, которые могут влиять на результаты измерений. Систематическая погрешность связана с постоянными факторами, которые могут приводить к смещению результатов в определенную сторону.
Взаимосвязь физических величин также может проявляться через уравнения и законы, которые описывают их свойства и взаимодействия. Например, закон Ома для электрического тока и напряжения, уравнение Ньютона для движения тела и т. д. Знание этих законов позволяет соотносить физические величины и прогнозировать результаты измерений при заданных условиях.
Таким образом, взаимосвязь физических величин в метрологии является фундаментальной для проведения точных и надежных измерений, обеспечивая основу для разработки методов и техник измерений, анализа результатов и установления их достоверности.
Значение физических величин для научных исследований
Физические величины играют важную роль в научных исследованиях, позволяя нам измерять, описывать и объяснять различные физические процессы. Они представляют собой конкретные числовые значения, которые можно измерить и записать в единицах измерения. Физические величины используются в различных областях науки, таких как физика, химия, биология и другие.
Одним из основных аспектов значимости физических величин для научных исследований является возможность создания объективного и точного описания исследуемых явлений и объектов. Благодаря измерению физических величин мы можем получить количественные данные, которые позволяют проводить сравнения, анализировать результаты экспериментов и формулировать законы и принципы. Это важно для разработки новых теорий и моделей, а также для определения причинно-следственных связей.
Кроме того, физические величины играют роль в измерительном процессе. С помощью измерений мы можем проверять гипотезы, подтверждать или опровергать теории, оценивать точность и надежность экспериментальных данных. Физические величины также позволяют создавать стандарты и установить согласованные системы единиц измерения, что необходимо для сравнения результатов измерений между разными лабораториями и исследовательскими группами.
Важно отметить, что физические величины имеют не только научное, но и практическое значение. Они используются в различных инженерных и технологических областях для проектирования и создания новых устройств, разработки новых материалов, контроля и измерения параметров в процессе производства и многое другое. Физические величины помогают создавать инновационные решения и применять их на практике, что способствует развитию науки и техники.
Таким образом, значимость физических величин для научных исследований трудно переоценить. Они являются ключевыми инструментами в измерениях и описании физических явлений, способствуют разработке новых теорий и моделей, а также находят широкое применение в практических областях.



