Магнитное поле является одним из фундаментальных понятий в физике. Оно окружает нас повсюду, влияя на множество аспектов нашей жизни. Но что такое объемная плотность энергии магнитного поля и как ее можно определить?
Объемная плотность энергии магнитного поля представляет собой меру энергетической активности магнитного поля в единице объема. Она определяется формулой:
u = (1/2μ)B²,
где u - объемная плотность энергии магнитного поля, μ - магнитная постоянная, B - магнитная индукция.
Эта формула позволяет вычислить объемную плотность энергии магнитного поля, используя известные значения магнитной индукции и магнитной постоянной. Она подтверждается множеством экспериментов, и является одним из основных законов электродинамики.
Объемная плотность энергии магнитного поля имеет важное значение в различных областях науки и техники. Например, она играет ключевую роль в электромагнитной совместимости и расчете энергетических параметров электрических и электронных устройств. Также она является основой для понимания принципов работы многих электромагнитных устройств, таких как электродвигатели и генераторы.
Физические основания плотности энергии магнитного поля
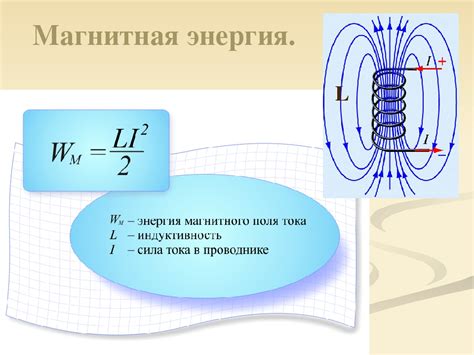
Физическая основа плотности энергии магнитного поля заключается в том, что магнитное поле обладает энергией, которая может быть использована для выполнения работы или передачи энергии другим системам. Эта энергия связана с движением заряженных частиц в магнитном поле, а также с взаимодействием магнитных полей с зарядами и другими полями.
Плотность энергии магнитного поля может быть определена путем интегрирования энергетической плотности по всему объему пространства. Для этого используется формула, в которой входят магнитная индукция и другие физические параметры.
| Формула для вычисления плотности энергии магнитного поля | Обозначение |
|---|---|
| W = (1/2) * B^2 * μ | W - плотность энергии магнитного поля |
В этой формуле B обозначает магнитную индукцию, а μ - магнитную постоянную, которая характеризует взаимодействие магнитных полей. Величина плотности энергии магнитного поля определяется только магнитной индукцией и не зависит от других физических параметров.
Плотность энергии магнитного поля является важной характеристикой магнитных полей и используется во многих областях науки и техники, включая электромагнитные системы, силовые и инженерные решения.
Закон Гаусса и плотность энергии магнитного поля
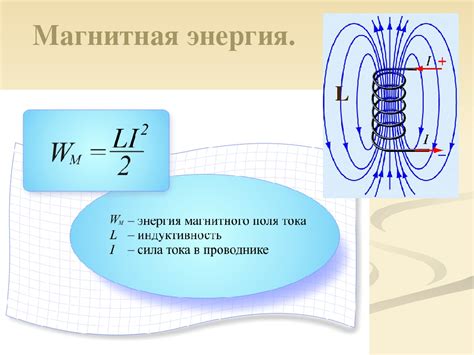
Математически, закон может быть записан в виде:
∮B·dS = 0,
где ∮ обозначает интеграл по замкнутой поверхности, B - вектор магнитной индукции, а dS - элемент площади поверхности.
На основе закона Гаусса можно получить уравнение для плотности энергии магнитного поля. Для этого рассмотрим замкнутую поверхность, охватывающую объем V, в котором находится магнитное поле.
Из формулы Закона Гаусса следует, что интеграл от вектора магнитной индукции B по замкнутой поверхности равен нулю:
∮B·dS = 0.
Разобьем этот интеграл на две части. Первую часть можно записать как:
∮B·dS = ∫B·dS = ∫B·ndS,
где ∫ обозначает интеграл по замкнутой поверхности, B - вектор магнитной индукции, dS - элемент площади поверхности, а n - единичная нормаль к поверхности.
Вторую часть можно записать как:
∮B·dS = ∫B·dS = ∫B·ndS = B∫ndS = B∫dS,
где B - модуль вектора магнитной индукции.
Учитывая, что элемент поверхности dS можно записать как площадь поверхности, деленную на ее объем, получим:
∮B·dS = B∫dS = BV,
где V - объем, охватываемый замкнутой поверхностью.
Таким образом, получаем уравнение:
BV = 0.
Из этого уравнения следует, что плотность энергии магнитного поля в объеме V равна нулю.
Таким образом, закон Гаусса позволяет определить, что плотность энергии магнитного поля в объеме равна нулю. Это означает, что магнитное поле не обладает энергией в отсутствии других полей или зарядов.
Различные методы определения объемной плотности энергии магнитного поля

Один из методов - это использование закона сохранения энергии. Согласно этому закону, изменение энергии магнитного поля в объемном элементе пространства равно работе, потраченной на перемещение зарядов через этот элемент. Таким образом, можно вычислить объемную плотность энергии магнитного поля, используя известные значения силы тока и магнитной индукции.
Другой метод - это использование физического явления намагниченности вещества. Когда вещество находится в магнитном поле, оно может намагничиваться и создавать собственное магнитное поле. Измеряя изменение магнитной индукции при наличии и отсутствии намагниченного вещества, можно определить объемную плотность энергии магнитного поля.
Третий метод - это использование силовых линий магнитного поля. Силовые линии представляют собой воображаемые линии, которые представляют направление и силу магнитного поля. Измеряя расстояние между силовыми линиями в объеме пространства, можно определить объемную плотность энергии магнитного поля.
| Метод | Принцип | Преимущества | Недостатки |
|---|---|---|---|
| Закон сохранения энергии | Измерение работы, потраченной на перемещение зарядов | Прост в использовании | Требуется точное измерение силы тока и магнитной индукции |
| Намагниченность вещества | Измерение изменения магнитной индукции при наличии и отсутствии намагниченного вещества | Не требуется измерение силы тока и магнитной индукции | Требуется наличие намагниченного вещества |
| Силовые линии магнитного поля | Измерение расстояния между силовыми линиями в объеме пространства | Не требуется измерение силы тока и магнитной индукции | Требуется точное измерение расстояния |
Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода определения объемной плотности энергии магнитного поля зависит от конкретных условий эксперимента и доступных средств.
Зависимость плотности энергии магнитного поля от магнитной индукции
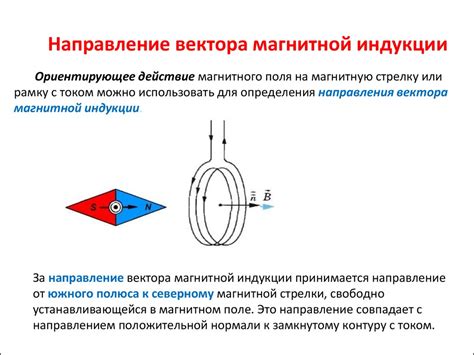
Данная плотность зависит от магнитной индукции, которая характеризует силу и направление магнитного поля в данной точке пространства. Чем больше магнитная индукция, тем выше плотность энергии магнитного поля.
Величина плотности энергии магнитного поля может быть вычислена по формуле:
W = (1/2μ₀) B²,
где W - плотность энергии магнитного поля, B - магнитная индукция, а μ₀ - магнитная постоянная.
Эта формула показывает, что плотность энергии магнитного поля пропорциональна квадрату магнитной индукции. Таким образом, увеличение магнитной индукции приводит к значительному возрастанию плотности энергии магнитного поля.
Зависимость плотности энергии магнитного поля от магнитной индукции имеет важные практические применения. Например, она используется для расчета энергетического потенциала магнитных систем, для определения мощности существующих и разрабатываемых устройств, а также для оптимизации энергетических процессов в магнитных системах.
Применение объемной плотности энергии магнитного поля в технологиях
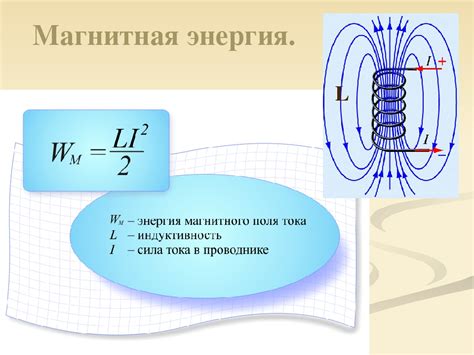
Объемная плотность энергии магнитного поля, измеряемая в джоулях на кубический метр, играет важную роль в современных технологиях. Эта величина описывает количественные характеристики энергии, содержащейся в единице объема магнитного поля.
Одно из наиболее распространенных применений объемной плотности энергии магнитного поля – это использование ее в магнитно-резонансной томографии (МРТ). В данной технологии с помощью магнитных полей создается подробное изображение внутренних органов и тканей человека. Энергия, хранящаяся в магнитном поле, позволяет получать высококачественные и четкие снимки, не наносящие вреда пациенту.
Также объемная плотность энергии магнитного поля применяется в электроэнергетике, в особенности в создании суперпроводящих магнитов и играет ключевую роль в исследованиях по созданию ядерных реакторов и электромагнитных ускорителей. Эта характеристика позволяет точно рассчитывать и контролировать энергетические параметры в различных технических устройствах.
Наряду с этим, объемная плотность энергии магнитного поля используется в производстве магнитных датчиков, моторов и генераторов, а также в системах беспроводной зарядки устройств. Благодаря возможности эффективной передачи энергии и малому расходу ресурсов, магнитное поле успешно применяется в передовых технологиях и способствует прогрессу в различных отраслях промышленности.



