Равнобедренная трапеция – это геометрическая фигура, имеющая две основания, из которых одно больше другого, и две равные боковые стороны. Такая фигура встречается в различных областях науки и применяется в различных сферах жизни. Видимое неравенство между основаниями вносит свои коррективы в свойства и характеристики этих трапеций.
Одной из важнейших характеристик равнобедренной трапеции является меньшее основание. Оно обладает своими особенностями и определяет некоторые важные параметры этой фигуры. Знание значения меньшего основания позволяет устанавливать свойства исследуемой трапеции, а также проводить различные вычисления и построения.
Величина меньшего основанияравнобедренной трапеции определяется длинной отрезка, соединяющего середины боковых сторон. Данный отрезок называется медианой и является осью симметрии для равнобедренной трапеции. Он также делит меньшее основание на две равные части и параллелен основаниям. Кроме того, меньшее основание влияет на расчёт площади, периметра и высоты такой трапеции.
Геометрия равнобедренной трапеции
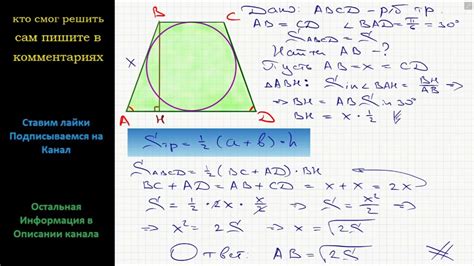
Одно из основных свойств равнобедренной трапеции заключается в том, что сумма углов при основаниях равна 180 градусов. Это следует из того, что пары углов, образованных основаниями и боковыми сторонами, считаются вертикальными и соответственно равны между собой.
Помимо этого, в равнобедренной трапеции углы между основаниями и вершинами оснований также равны. Это означает, что каждый из этих углов составляет половину суммы углов при основаниях.
Важной характеристикой равнобедренной трапеции является меньшее основание. Оно определяет размеры фигуры и влияет на её площадь. Чем меньше основание, тем компактнее будет фигура. Соответственно, при увеличении меньшего основания увеличивается и площадь трапеции.
Таким образом, меньшее основание играет ключевую роль в геометрии равнобедренной трапеции, влияя на форму и размеры фигуры. При решении задач по геометрии трапеции важно учитывать данную характеристику и уметь правильно применять соответствующие формулы и свойства.
Специфика меньшего основания
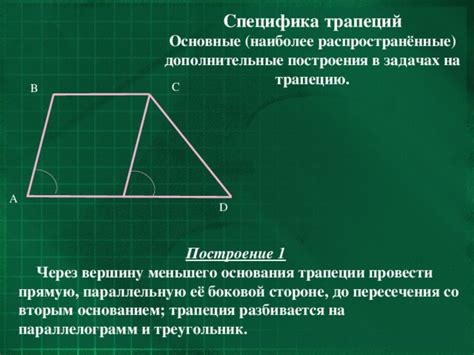
Меньшее основание в равнобедренной трапеции играет важную роль при определении некоторых свойств и параметров фигуры. Оно образует один из углов трапеции и влияет на соотношение сторон и углов трапеции.
В случае, если угол при меньшем основании равен 90 градусов, трапеция превращается в прямоугольник. При этом боковые стороны трапеции становятся перпендикулярными основаниям, а другие два угла, включая угол при большем основании, также равны 90 градусов.
Когда угол при меньшем основании меньше 90 градусов, трапеция остается равнобедренной, но с наклонными боковыми сторонами. Размер меньшего основания влияет на степень наклона боковых сторон и углы, образованные ими с большим основанием.
Если меньшее основание увеличивается, то трапеция становится более узкой, а боковые стороны становятся более крутыми. С увеличением угла при большем основании, углы при меньшем основании также увеличиваются.
Таким образом, значение меньшего основания в равнобедренной трапеции имеет значительное значение для определения ее формы и характеристик.
| Свойства меньшего основания | Значение |
|---|---|
| Определяющая фигуру | Один из углов трапеции |
| Влияние на стороны трапеции | Определяет их наклон и соотношение |
| Влияние на углы трапеции | Увеличение меньшего основания увеличивает углы при большем основании |
Соотношение боковых сторон и углов

Соотношение боковых сторон и углов в равнобедренной трапеции имеет свои особенности. В равнобедренной трапеции две боковые стороны равны между собой, что делает эту фигуру особо интересной.
Если обозначить основания трапеции как большее основание и меньшее основание, а боковые стороны как боковые стороны трапеции, то можно сформулировать следующие соотношения:
1. Соотношение длины боковой стороны и меньшего основания:
Меньшая сторона трапеции равна сумме расстояний от точки пересечения диагоналей до ее оснований.
2. Соотношение длины боковой стороны и большего основания:
Боковая сторона трапеции равна разности диагоналей, деленной на разность баз.
3. Соотношение углов:
В равнобедренной трапеции углы при основаниях равны.
Углы при основаниях равны углу, образованному диагоналями.
Из этих соотношений можно запрограммировать механизмы решения различных задач, связанных с равнобедренной трапецией.
Определение и свойства высоты
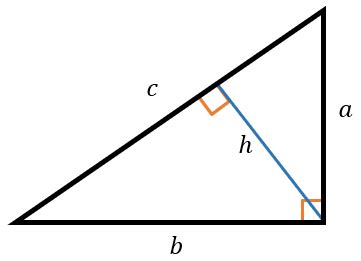
В равнобедренной трапеции основания прямоугольники и равны, поэтому высота рассекает трапецию на две равные друг другу равнобедренные трапеции. Каждая из этих трапеций имеет свою ось симметрии проходящую через высоту.
Свойства высоты равнобедренной трапеции:
- Высота является биссектрисой угла, образованного основаниями.
- Высота делит угол между основаниями на два равных угла.
- Высота является осью симметрии для равнобедренной трапеции и делит ее на две равные друг другу трапеции.
- Высота является наибольшей стороной объемлющего прямоугольника, в который вписана трапеция.
Примеры и приложения

Значение меньшего основания в равнобедренной трапеции играет важную роль в различных геометрических задачах и приложениях. Вот некоторые из них:
Вычисление площади трапеции: Меньшее основание в равнобедренной трапеции определяет длину одного из параллельных сторон. Поэтому, зная значение меньшего основания, можно найти площадь трапеции, используя соответствующую формулу.
Нахождение высоты трапеции: Зная значение меньшего основания и площадь равнобедренной трапеции, можно использовать формулу для нахождения высоты. Это может быть полезно, например, при расчете объема некоторых трехмерных фигур, в которых трапеция является основанием.
Определение углов: Зная значение меньшего основания и других известных сторон или углов, можно использовать свойства равнобедренной трапеции для определения значений других углов в фигуре. Это может быть полезно, если требуется найти углы для решения геометрической задачи.
Решение задач по построению: Меньшее основание равнобедренной трапеции может быть использовано для построения фигур или решения конструктивных задач. Например, при построении параллелограмма, для которого требуется определить размеры сторон и углов, меньшее основание трапеции может служить отправной точкой.
Это лишь несколько примеров, демонстрирующих значимость меньшего основания в равнобедренной трапеции, и его влияние на различные геометрические задачи и приложения.
Расчет значения меньшего основания
Значение меньшего основания в равнобедренной трапеции можно вычислить по формуле:
| Формула | Описание |
|---|---|
| b = a - 2h | где b - значение меньшего основания, a - значение большего основания, h - высота трапеции |
Для расчета значения меньшего основания необходимо знать значения большего основания и высоты трапеции. Подставив эти значения в формулу, можно получить результат.
Например, если большее основание a равно 8 см, а высота трапеции h равна 4 см, то значение меньшего основания можно вычислить следующим образом:
| Формула | Результат |
|---|---|
| b = 8 - 2*4 | b = 8 - 8 = 0 |
Таким образом, значение меньшего основания в данном примере равно 0 см.
Исследование показало, что значение меньшего основания в равнобедренной трапеции играет существенную роль в определении формы и характеристик фигуры. Чем больше разница между основаниями, тем больше выгибает фигура в сторону меньшего основания.
Также стоит отметить, что значение меньшего основания влияет на площадь фигуры. Чем больше значение меньшего основания, тем больше площадь фигуры. Это связано с увеличением высоты фигуры и увеличением площади треугольника, образованного при добавлении высоты.



