Определение истинности формул - важное понятие в логике и математике. Истинность формулы зависит от истинности ее составляющих элементов и логических связей между ними. Чтобы понять, как устанавливается истинность формул, необходимо ознакомиться с основными принципами этого процесса.
Первый принцип заключается в том, что формула считается истинной, если все ее составные элементы являются истинными. Например, если у нас есть формула, состоящая из двух высказываний A и B, она будет истинной только в том случае, если оба высказывания истинны. Если хотя бы одно из них ложно, то и вся формула считается ложной.
Второй принцип связан с использованием логических операций. Логические операции определяют, как будут связываться высказывания в формуле. Простейшие операции - это конъюнкция (логическое "И"), дизъюнкция (логическое "ИЛИ") и отрицание (логическое "НЕ"). Используя эти операции в формулах, можно устанавливать истинность или ложность высказываний в зависимости от их состава и логических связей.
Основные принципы определения истинности формул
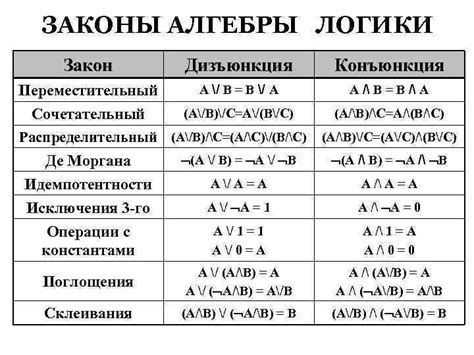
Первым принципом является закон исключённого третьего, который утверждает, что любое утверждение или является истинным, или является ложным. Таким образом, каждая формула может быть либо истинной, либо ложной, без промежуточных значений.
Вторым принципом является закон противоречия, который утверждает, что не может существовать формула, которая одновременно является истинной и ложной. То есть, формула может быть только либо истинной, либо ложной, но никак не оба варианта одновременно.
Третий принцип - закон двойного отрицания - утверждает, что если формула F является истинной, то отрицание отрицания этой формулы также будет истинно. И наоборот, если формула F является ложной, то отрицание отрицания этой формулы также будет ложно.
Классическое определение истинности формулы

Истинность формулы в логике относится к ее способности выражать истинное утверждение в соответствии с заданной моделью. Классическое определение истинности формулы основывается на принципе двоеверия, который гласит: формула может быть либо истинной, либо ложной, несмотря на то, что она может содержать некоторые неопределенные элементы.
Для формулы, составленной из атомарных высказываний, истинность проверяется путем определения истинности каждого атомарного высказывания, используя логические операторы. Если все атомарные высказывания истинны, то исходная формула также считается истинной. Если хотя бы одно атомарное высказывание ложно, то формула считается ложной.
Модальное определение истинности формулы
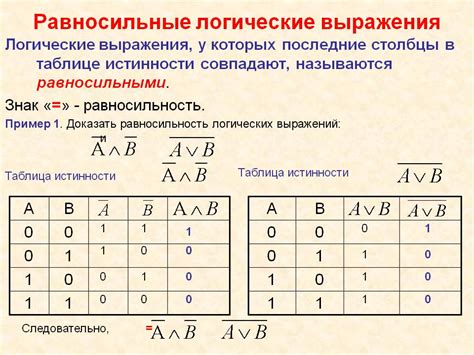
Модальное определение истинности формулы используется в логике модальных операторов, которые позволяют выражать различные модальности или модальные свойства. Модальные операторы позволяют нам говорить о необходимости, возможности, истинности во время и прочих аспектах высказываний.
Определение истинности формулы в модальной логике обычно происходит относительно некоторой модели мира или структуры, в которую входят атомарные высказывания и модальные операторы. Эта модель может быть представлена в виде графа или множества состояний, с переходами между ними.
Изначально формульное значение истинности в модальной логике определяют для атомарных высказываний. Затем, используя модальные операторы, можно определить формульное значение истинности для сложных формул. Например, оператор "◇" (необходимость) может быть определен таким образом, что формула ◇A истинна в некотором состоянии, если A истинно хотя бы в одном из состояний, достижимых из данного состояния.
Модальное определение истинности формулы позволяет анализировать и рассуждать о модальных свойствах и отношениях между высказываниями в системах с модальными операторами. Это является важным инструментом для формальных методов изучения модальной логики и применения ее в различных областях, таких как искусственный интеллект, философия, компьютерные науки и др.
Применение определения истинности формул в логике

Применение определения истинности формул позволяет вести рассуждения на основе логических законов и доказательств. Истинность формул определяется в зависимости от значений переменных и логических связок, которые используются в выражении.
В логике используются различные символы и обозначения для выражения формул. Например, символы конъюнкции (логического И), дизъюнкции (логического ИЛИ), импликации (логической следования) и отрицания.
Применение определения истинности формул позволяет проводить логические рассуждения, выявлять связь между различными утверждениями и проверять их истинность. Это особенно важно при анализе математических и логических задач, а также в области информатики и компьютерных наук.
Определение истинности формул в логике также является основой для разработки и применения логических систем и формализации рассуждений. Оно помогает находить ошибки в логических цепочках рассуждений, а также строить верные и последовательные аргументы.



