Омега - это один из самых важных понятий в физике, которое широко используется при изучении движения. В динамике и кинематике омега обозначает угловую скорость, то есть скорость, с которой тело вращается около своей оси. Она измеряется в радианах за секунду и играет важную роль в описании различных физических явлений.
Омега обозначается символом ω и является векторной величиной, то есть имеет как величину, так и направление. Она показывает, как быстро и в какую сторону вращается тело. Положительное направление омеги связано с против часовой стрелки вращением, а отрицательное - с по часовой стрелке.
Для лучшего понимания можно привести простой пример. Рассмотрим задачу о колесе, которое прокатывается по горизонтальной поверхности без скольжения. Угловая скорость ω этого колеса будет равна отношению угла поворота на временной интервал. Если колесо повернулось на один радиан за одну секунду, то его угловая скорость будет равна одному радиану в секунду.
Что такое Омега в физике при движении?

В физике Омега обычно обозначает угловую скорость при вращательном движении. Угловая скорость определяет скорость изменения угла поворота объекта.
Угловая скорость обычно измеряется в радианах в секунду (рад/с). Она показывает, насколько быстро объект вращается вокруг оси. Если объект вращается с постоянной угловой скоростью, это означает, что он поворачивается на один и тот же угол за единицу времени.
Угловая скорость связана со скоростью линейного движения через радиус объекта. Если радиус известен, можно вычислить линейную скорость объекта, умножив его радиус на угловую скорость.
Угловая скорость имеет особое значение в механике твердого тела и динамике, где вращательное движение играет важную роль. Угловая скорость используется для описания вращения колес, роторов, валов, спутников и других объектов, которые вращаются вокруг осей.
В общем случае, угловая скорость может изменяться во времени, и в этом случае используется производная от угла поворота по времени, которая называется угловым ускорением и обозначается символом альфа (α).
Омега: определение и значение в физике

Омега измеряется в радианах в секунду (рад/с). Положительное значение омеги указывает на движение против часовой стрелки, а отрицательное значение обозначает движение по часовой стрелке. Величина омеги также может быть положительной или отрицательной, в зависимости от направления вращения или движения тела.
Значение омеги имеет большое значение при изучении механики и динамики. Например, для вычисления линейной скорости тела можно использовать формулу: v = ω * r, где v - линейная скорость, ω - угловая скорость, r - радиус вращения тела.
Омегу также можно использовать для определения периода или частоты движения тела. Период обратно пропорционален омеге, а частота, наоборот, пропорциональна омеге. Формулы для вычисления периода и частоты могут быть записаны следующим образом: T = 2π/ω и f = ω/2π, где T - период, f - частота.
Кроме того, омега может быть использована для определения углового ускорения тела. Угловое ускорение (α) является изменением угловой скорости по времени и может быть рассчитано по формуле: α = ω2 - ω1 / t, где ω2 и ω1 - конечная и начальная угловые скорости, t - время изменения угла.
Таким образом, омега является важным понятием в физике, позволяющим описывать и анализировать движение и вращение тел. Знание омеги и связанных с ней формул позволяет получить информацию о скорости, ускорении, периоде и частоте движения тела.
Формула и физическая интерпретация

В физике при движении, формула для угловой скорости ω определяет угловую скорость объекта. Угловая скорость показывает, как быстро объект вращается вокруг оси, и измеряется в радианах в секунду (рад/с).
Формула для угловой скорости выглядит следующим образом:
ω = δθ/δt
где ω - угловая скорость, δθ - изменение угла за промежуток времени δt. Угловую скорость можно также выразить через период T:
ω = 2π / T
Физическая интерпретация угловой скорости зависит от конкретной системы или объекта. Например, при рассмотрении вращения колеса автомобиля, угловая скорость будет показывать, как быстро колесо вращается вокруг своей оси. Для планеты, угловая скорость будет характеризовать ее вращение вокруг своей оси в пространстве. В общем случае, угловая скорость позволяет описывать вращательное движение объектов и является важной величиной в физике.
Примеры применения Омеги в физике

| Пример | Описание |
|---|---|
| Движение вращения | В механике Омега используется для описания скорости вращения тела. Она определяет скорость изменения угла поворота объекта в единицу времени. Например, при исследовании вращения колеса велосипеда или вращения планет вокруг своей оси Омега используется для определения и анализа скорости вращения. |
| Сложение скоростей | Омега также используется при сложении скоростей в физике. Когда объект движется как вращается вокруг оси, его линейная скорость может быть определена в терминах Омеги. Это помогает в определении и анализе общей скорости объекта, учитывая и линейную, и угловую скорости. |
| Магнитные поля | В физике Омега также используется для описания поворота заряженных частиц в магнитных полях. При переходе заряженной частицы через магнитное поле, применяется сила Лоренца, где Омега играет роль и определяет частоту обращения заряженной частицы. |
Это лишь некоторые примеры применения Омеги в физике. Этот параметр имеет широкий спектр применений и встречается во многих других областях, таких как астрономия, электротехника и динамика систем.
Первый пример: Угловая скорость вращения
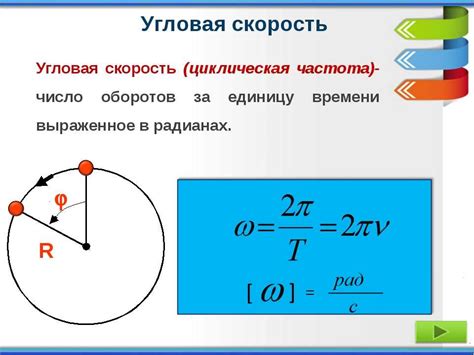
Рассмотрим пример смещения точки на поверхности вращающегося объекта. Пусть точка находится на расстоянии R от центра вращения. Когда объект полностью совершает один оборот, точка также описывает полный оборот вокруг центра. Угловая скорость, обозначаемая символом ω, определяется как отношение угла поворота к промежутку времени, за которое произошло вращение.
Угловую скорость можно выразить в радианах в секунду (рад/с). Величина угловой скорости зависит как от линейной скорости точки, так и от расстояния R от центра вращения. Формула для расчета угловой скорости представлена следующим образом:
ω = v / R,
где v - линейная скорость точки, R - расстояние от центра вращения.
Таким образом, угловая скорость вращения зависит от скорости и расстояния от центра вращения, что позволяет описать движение точек на поверхности вращающегося объекта.
Второй пример: Скорость прецессии
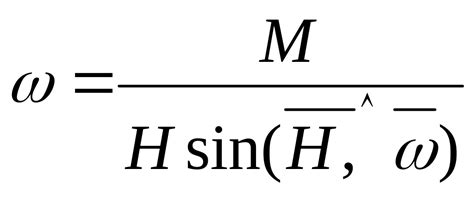
Когда гироскоп вращается, он обладает свойством прецессии - изменения ориентации оси вращения под действием внешнего вращательного момента. Эта прецессия может быть измерена скоростью прецессии, которая выражается в радианах в секунду.
Скорость прецессии зависит от нескольких факторов, включая момент инерции гироскопа, его угловую скорость, а также воздействие внешних сил. Если гироскоп находится в неподвижном состоянии, то его скорость прецессии будет равна нулю.
Например, рассмотрим гироскоп, вращающийся со скоростью 1000 радиан в секунду. Пусть момент инерции гироскопа равен 0.5 кг * м^2. В этом случае, скорость прецессии может быть рассчитана с использованием следующей формулы:
где - скорость прецессии, - момент вращающего момента, - момент инерции гироскопа.
Подставляя известные значения в формулу, получим:
что означает, что скорость прецессии гироскопа равна 2000 радиан в секунду. Это означает, что ось вращения гироскопа будет медленно изменять свое положение в пространстве.
Третий пример: Ангулярное ускорение
Рассмотрим пример. Представим, что у нас есть каток, который начинает вращаться вокруг вертикальной оси. В начальный момент времени каток имеет нулевую угловую скорость, а через некоторое время его скорость увеличивается до определенного значения. В этом случае у катка происходит ангулярное ускорение - его скорость поворота возрастает.
Для того, чтобы вычислить ангулярное ускорение, можно использовать следующую формулу:
α = Δω / Δt
где α - ангулярное ускорение, Δω - изменение угловой скорости, а Δt - изменение времени.
Таким образом, ангулярное ускорение позволяет определить, насколько быстро меняется угловая скорость вращения тела, и может быть использовано для анализа различных физических явлений, связанных с вращательным движением.



