Округление – это математическая операция, которая заключается в приближении числа к ближайшему значению с меньшим количеством знаков после запятой. Оно широко применяется в различных сферах деятельности, таких как финансовый анализ, статистика, программирование и многое другое. Округление используется для упрощения числовых данных и удобства их восприятия.
Округление часто применяется при работе с десятичными дробями, которые представляют собой числа с десятичной точкой. Они могут быть представлены как положительными, так и отрицательными значениями. Округление дробных чисел может проводиться в различных направлениях: в большую сторону, в меньшую сторону или к ближайшему значению. Выбор способа округления зависит от требований и контекста, в котором применяется округление.
Зачем же округлять десятичные дроби? Причин может быть много. С одной стороны, округление позволяет сократить количество знаков после запятой и сделать числа более компактными и удобочитаемыми. Это особенно полезно при работе с большими наборами данных или при представлении результатов вычислений.
Округление и его значение в математике
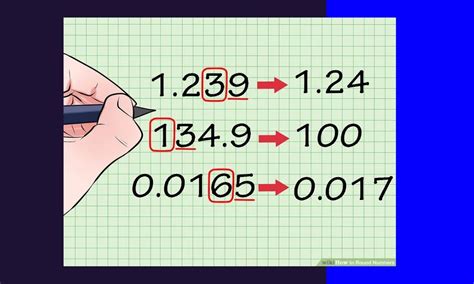
Округление осуществляется путем приближения числа до определенного порядка. Наиболее распространенным методом округления является округление до целого числа. В этом случае, если десятичная дробь имеет десятичную часть меньше или равную 0.5, она округляется вниз, а если десятичная часть больше 0.5, то дробь округляется вверх.
Округление имеет большое значение при работе с деньгами, где точность очень важна. Например, при расчете налогов или финансовых операций округление может существенно повлиять на результат и привести к существенным различиям в конечном итоге.
Однако, округление не всегда является идеальным методом представления десятичных дробей и может привести к ошибкам или потере информации. Поэтому, при округлении необходимо учитывать контекст и цель применения округления.
Округление чисел: как и зачем это делается?

Округление применяется в различных областях жизни, включая математику, финансы, программирование и т.д. Главная цель округления - сделать числа более удобными для работы и понимания.
Зачем округлять десятичные числа? Округление позволяет упростить числовые вычисления, уточнить результаты и сделать их более понятными для людей. Например, при работе с деньгами или измерением физических величин удобно округлять до определенного количества знаков после запятой.
Существует несколько правил округления, включая правила "ближайшего четного", "вверх", "вниз" и т.д. В зависимости от требований и контекста, выбирается соответствующее правило округления.
Пример:
округление числа 3.14159 по правилу "вверх" до двух знаков после запятой даст результат 3.15.
округление числа 0.75 по правилу "ближайшего четного" до одного знака после запятой даст результат 0.8.
Важно помнить, что округление может привести к некоторой потере точности, особенно если число содержит значительное количество десятичных знаков. Также стоит учитывать контекст округления и его влияние на результат вычислений.
Округление десятичных дробей: основные правила
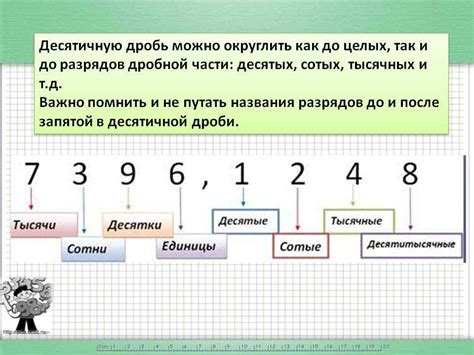
В основе округления лежат определенные правила, которые следует соблюдать при округлении десятичных дробей. Вот основные из них:
1. Округление до ближайшего целого числа:
Если дробная часть числа больше или равна 0,5, то число округляется до следующего большего целого числа. Например, число 3,6 округляется до 4.
Если дробная часть числа меньше 0,5, то число округляется до ближайшего меньшего целого числа. Например, число 2,3 округляется до 2.
2. Округление до числа с определенным количеством знаков после запятой:
Для округления до определенного количества знаков после запятой, сначала находим число с требуемым количеством знаков после запятой и затем округляем его согласно первому правилу. Например, для округления числа 3,146 до одного знака после запятой, сначала получаем число 3,1 и затем округляем его до 3.
3. Округление к ближайшему числу имеющему все нули после запятой:
В некоторых случаях требуется округлить число так, чтобы все знаки после запятой были нулями. В этом случае число округляется до ближайшего числа, которое имеет все нули после запятой. Например, число 3,72 округляется до 4, так как 4 имеет все нули после запятой.
Знание основных правил округления десятичных дробей позволит вам контролировать точность и удобство использования чисел в различных ситуациях.
Округление в математических операциях: с чем связана необходимость округления?

Несмотря на то, что десятичные дроби позволяют представить числа с большей точностью, чем целые числа, часто возникает необходимость упростить результаты математических операций. Например, если вам нужно посчитать общую сумму покупок в магазине, то результат может быть очень точным, но в реальной жизни люди обычно округляют до двух десятичных знаков: копеек.
В некоторых случаях округление может быть источником погрешностей и ошибок. При выполнении последовательных округлений результат может существенно отличаться от ожидаемого. Поэтому при округлении следует учитывать контекст и требования к точности получаемого результата.
| Операция | Пример | Результат без округления | Результат с округлением |
|---|---|---|---|
| Сложение | 4.67 + 2.51 | 7.18 | 7.2 |
| Вычитание | 5.43 - 3.29 | 2.14 | 2.1 |
| Умножение | 3.25 * 1.9 | 6.18 | 6.2 |
| Деление | 7.84 / 2.9 | 2.703448275862069 | 2.70 |
Из приведенных примеров видно, что округление позволяет записать результаты математических операций в более простой и понятной форме. Также следует помнить, что округление может изменять значение числа, поэтому его применение требует внимательности.
Округление в финансовой сфере: почему точность до копейки так важна?
В финансовой сфере, где каждая копейка имеет огромное значение, округление играет ключевую роль. Оно позволяет установить точность до мельчайших деталей и добиться максимальной достоверности и надежности финансовых данных. Точное округление до копейки позволяет избежать неточностей и ошибок при проведении финансовых операций.
Одной из главных причин, почему точность округления до копейки столь важна в финансовой сфере, является необходимость получения верных результатов при подсчете и учете финансовых средств. Например, при проведении бухгалтерских расчетов или составлении отчетов, любая неточность в округлении может привести к серьезным последствиям, таким как неправильное начисление процентов, переплата или недоплата по налогам и штрафы.
Округление до копейки важно также при работе с банковскими операциями. Представьте себе ситуацию, когда ваш банковский счет имеет недостоверную информацию о сумме находящихся на нем средств. Это может привести к задержкам или отказам в проведении платежей, переводах или операций с кредитами.
В конечном итоге, точность округления до копейки отражает профессионализм и ответственность финансовых специалистов и учреждений. Чтобы обеспечить достоверность и надежность финансового анализа, бухгалтерии и финансовой отчетности, округление до копейки является неотъемлемой частью работы в финансовой сфере.
Округление и его влияние на статистику: как округление может искажать данные?

В статистике округление играет важную роль при обработке и анализе данных. Округление десятичных дробей позволяет упростить числа и сделать их более удобными для восприятия и дальнейшего использования. Однако, не всегда округление оказывается безвредным и может внести искажения в итоговую статистику.
Когда мы округляем десятичные дроби, мы отбрасываем дробную часть числа и оставляем только целую. Это может привести к искажению данных, особенно в случаях, когда точность имеет большое значение. Например, если мы округлим до ближайшего целого все значения в статистике, то можем получить искаженные результаты.
Другим примером искажения данных может быть округление до наименьшего или наибольшего значения. Если мы округлим все значения в большую сторону, то мы будем получать завышенные значения в статистике. В этом случае, представленные данные будут необъективными и искаженными. То же самое происходит и в обратной ситуации, когда мы округляем значения до наименьшего. Полученные результаты будут заниженными и история, которую они рассказывают, может быть искажена.
Округление в программировании и его роль в вычислениях

Когда в программировании выполняются арифметические операции с десятичными числами, результат может быть представлен с большим числом знаков после запятой. Округление позволяет упростить результаты, чтобы они были более понятными и удобными для использования.
В программировании существуют различные методы округления чисел, такие как:
- Округление вверх (round up) - число округляется до следующего наибольшего значения.
- Округление вниз (round down) - число округляется до следующего наименьшего значения.
- Округление к ближайшему четному (round to even) - число округляется до ближайшего четного значения.
- Отбрасывание дробной части (truncation) - дробная часть числа просто отбрасывается.
- Приближение к нулю (round towards zero) - число округляется к нулю.
Выбор метода округления зависит от требований конкретной задачи и контекста вычислений. Некоторые задачи могут требовать максимальной точности, в то время как другие могут предпочитать более простое округление для упрощения и ускорения вычислений.
Округление имеет важное значение в финансовой сфере, где точность вычислений является критической. Например, при расчете налогов или финансовых операций необходимо использовать точное округление для избежания ошибок.
Таким образом, округление в программировании является неотъемлемой частью вычислительных операций, которая позволяет работать с десятичными числами с нужной точностью и простотой использования результатов.
Округление и его применение в повседневной жизни

Округление широко применяется в финансовых операциях. Например, при расчете налогов или зарплаты, сумма округляется до целого числа, чтобы избежать неприятных дробных центов. В магазинах округление используется для подсчета суммы покупки и выдачи сдачи.
Округление играет важную роль при расчете процентов. Например, при расчете процентов по вкладу в банке, сумма депозита может быть округлена до ближайшего большего целого числа для более точного расчета процентов.
Округление также применяется в торговле и производстве. Например, при производстве продуктов массового потребления, округление используется для определения количества сырья или компонентов, необходимых для производства. В розничной торговле, округление используется при определении цены товара на полке.
Округление также важно в научных и статистических исследованиях. Например, при анализе данных, округление используется для упрощения и интерпретации результатов. В физических и инженерных расчетах, округление применяется для более точных вычислений.
В общем, округление – это неотъемлемая часть повседневной жизни, которая помогает нам делать точные расчеты и принимать решения на основе округленных чисел. Без использования округления, многие расчеты были бы гораздо сложнее и менее точными.



