Понятие симметрии тесно связано с геометрией и математикой. В геометрии, точки симметричны относительно другой точки, если они равноудалены от данной точки и лежат на прямой, проходящей через эту точку. Это значит, что при проведении прямой линии из данной точки до каждой из симметричных точек, расстояние будет одинаковым.
Симметричные точки являются друг для друга спутниками, они отражают друг друга относительно данной точки. Например, точка А и точка В симметричны относительно точки О, если расстояние от точки О до точки А равно расстоянию от точки О до точки В. Точка О является центром симметрии, а прямая, проходящая через точку О, называется осью симметрии.
Понятие симметрии является фундаментальным в геометрии и применяется в различных задачах и решениях. Оно нашло свое применение в архитектуре, дизайне и изобразительном искусстве. Понимание симметрии и умение распознавать симметричные отношения между точками помогают увидеть красоту форм и структур вокруг нас.
Что такое симметричные точки?

Центр симметрии - это точка, относительно которой происходит симметричное отображение. Это может быть середина отрезка, середина окружности или любая другая точка на плоскости.
Симметрия является важным концептом в математике и геометрии. Она присутствует во многих объектах и структурах - от геометрических фигур до рисунков и символов.
Понимание симметрии и симметричных точек помогает нам анализировать и классифицировать объекты по их форме и свойствам. Например, симметричные точки могут быть использованы для создания симметричной картинки или изображения.
Симметричность точек
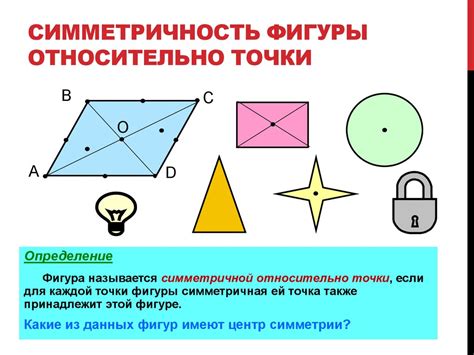
Точки симметричны относительно другой точки, если они находятся на одинаковом расстоянии от этой точки, но по разные стороны от нее. Мы можем найти точку симметричную данной точке относительно другой точки, проведя прямую линию, которая проходит через обе точки и перпендикулярна линии, соединяющей данные точки.
Точки, симметричные относительно другой точки, имеют одинаковые координаты по обоим осям, но с разными знаками. Например, точка (3,5) симметрична относительно точки (1,2), если они находятся на одинаковом расстоянии от точки (1,2), но выше и ниже ее соответственно.
Симметрия является важным понятием в математике и используется, например, при изучении геометрии и алгебры. Она помогает нам находить сходство и упрощать решение задач, связанных с расположением точек и объектов в пространстве.
Принцип симметрии
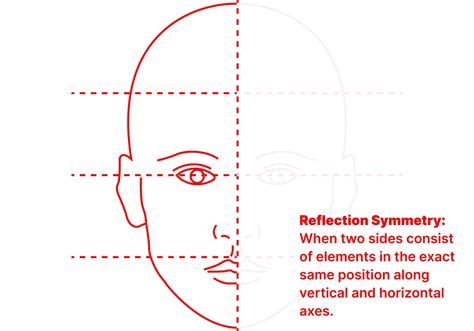
Принцип симметрии используется для определения понятия "точки симметрична относительно другой точки". Этот принцип заключается в том, что если точка А симметрична относительно точки В, то расстояние от точки А до точки В равно расстоянию от точки В до точки А. Это означает, что точка А и точка В находятся на одинаковом расстоянии от оси симметрии, которая проходит через точку, относительно которой определяется симметрия.
Примером принципа симметрии может служить изображение бабочки. Если взять точку на левом крыле бабочки и точку, симметричную относительно оси симметрии бабочки, которая проходит по ее телу, то расстояние от выбранной точки до оси симметрии будет равно расстоянию от оси симметрии до точки, симметричной к выбранной точке.
Принцип симметрии является важным понятием в геометрии и имеет множество применений. Он используется при создании симметричных фигур, построении отражений и определении симметричных точек относительно других объектов.
Симметричность точек относительно другой точки

Точки симметричны относительно другой точки, если каждая из них находится на одинаковом расстоянии от этой точки. Визуально это означает, что если нарисовать линию, соединяющую каждую из этих точек с этой особой точкой, то эти линии будут равными и будут образовывать углы одинаковой величины.
Математически, чтобы точки были симметричны относительно другой точки, нужно, чтобы координаты каждой точки в отношении этой особой точки x0, y0 удовлетворяли формулам:
x = 2*x0 - x1
y = 2*y0 - y1
где (x1, y1) - координаты последней точки, (x, y) - координаты симметричной точки.
Симметрия точек относительно другой точки широко применяется в различных областях, включая геометрию, физику, компьютерную графику и дизайн. Она позволяет создавать сбалансированные и эстетически приятные композиции, а также упрощает решение задач, связанных с отражением и поворотом объектов.
Ось симметрии
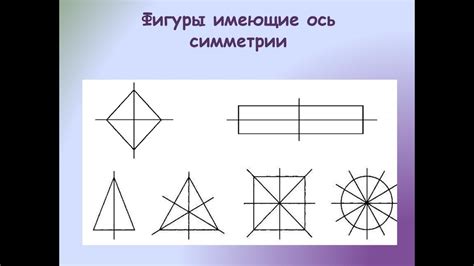
Когда объект имеет ось симметрии, его часть слева от оси выглядит идентичной части справа от оси, если перевернуть его вдоль оси. Таким образом, ось симметрии делит объект на две равные половины, которые отображают друг друга.
Ось симметрии может быть горизонтальной, вертикальной или диагональной в зависимости от положения фигуры. Например, в квадрате, прямоугольнике или окружности горизонтальная и вертикальная оси симметрии пересекаются в центре фигуры, тогда как в равнобедренном треугольнике диагональная ось симметрии проходит через вершину и середину основания.
Ось симметрии важна для определения симметричных точек относительно другой точки. Для двух точек быть симметричными относительно оси симметрии, расстояние от каждой из точек до оси должно быть равным. В математике ось симметрии играет важную роль в геометрии, симметрии и алгебре.
Как определить симметричные точки?
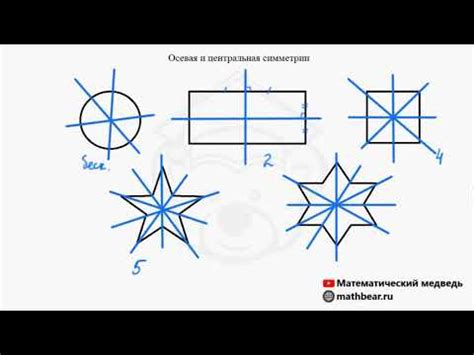
Симметрией называется свойство геометрической фигуры сохранять форму и размер при отражении относительно оси, плоскости или точки. В случае, когда рассматриваются точки, симметричность может быть определена относительно другой точки.
Для определения симметричных точек относительно другой точки необходимо проверить выполнение следующего условия: расстояние от заданной точки до первой точки равно расстоянию от заданной точки до второй точки. Иными словами, если точки A и B симметричны относительно точки O, то расстояние OA равно расстоянию OB.
Кроме того, для того чтобы точки были симметричными, необходимо, чтобы их относительное положение относительно заданной точки сохранялось при отражении. Если точки симметричны относительно точки O, то отношение между координатами точек A и B по отношению к точке O сохраняется: если координаты точки A равны (x1, y1), а точки B равны (x2, y2), то x1 - xO = xO - x2 и y1 - yO = yO - y2.
Для более наглядного представления симметричных точек, можно отобразить их на координатной плоскости. При отражении точек относительно другой точки, можно видеть, как они симметрично располагаются относительно оси, проведенной через данную точку. Таким образом, симметрия визуально проявляется в симметричном расположении точек относительно оси, проходящей через заданную точку.
Примеры симметричных точек

Точки симметричны относительно другой точки, если отрезок, их соединяющий, делится на две равные части, и оси, проходящие через эти точки, перпендикулярны друг другу. Вот несколько примеров симметричных точек:
- Точка А(2,3) и её симметричная относительно точки В(-2,3) находятся на одинаковом расстоянии от оси OX и имеют одинаковую координату Y.
- Точка К(5,-1) и её симметричная относительно точки M(-5,-1) лежат на одной прямой и находятся на равном расстоянии от вертикальной оси OY.
- Точка P(0,0) и её симметричная относительно точки Q(0,5) также находятся на одной прямой и имеют одинаковую координату X.
В каждом из этих примеров, две симметричные точки симметричны относительно третьей точки, тем самым обладая схожими свойствами по отношению к осям координат. Это свойство симметрии может быть полезно в различных математических и геометрических задачах.
Значение симметричных точек в математике

Одним из применений симметрии является нахождение симметричной точки относительно данной точки на плоскости. Для этого необходимо найти отрезок, соединяющий данную точку и симметричную ей точку, и продлить его в обратном направлении. Точка пересечения данного отрезка с продолжением прямой становится симметричной точкой.
Симметрия также находит применение в решении различных задач. Например, можно использовать симметрию для построения перпендикуляра к заданной прямой. Для этого достаточно построить симметричную точку относительно данной точки и соединить ее с исходной точкой. Полученная прямая будет перпендикулярной к исходной.
Важно отметить, что симметричные точки имеют одинаковое расстояние от данной точки. Это свойство позволяет использовать симметрию в нахождении середины отрезка. Для этого необходимо построить симметричную точку относительно одного из концов отрезка и соединить ее с другим концом. Перпендикуляр, проведенный к такой полученной прямой через точку, является серединой исходного отрезка.



