Математика - это один из основных предметов, изучаемых в школе. Второй класс - это время, когда дети начинают знакомиться с обратными данными и осваивать базовые математические понятия и правила.
Обратные данные - это такие числа, которые в сумме дают единицу. Например, 5 и -5 являются обратными данными, так как их сумма равна нулю. Знание обратных данных позволяет выполнять различные операции, такие как сложение и вычитание, а также решать уравнения.
Но как понять и запомнить, какие числа являются обратными данными? На помощь приходят правила. Первое правило гласит, что число и его обратное должны иметь одинаковую абсолютную величину, но противоположный знак. Например, если у нас есть число 7, то его обратное будет -7, так как 7 и -7 имеют одинаковую величину (7) и разные знаки (+ и -).
Второе правило гласит, что сумма числа и его обратного всегда равна нулю. Например, 7 + (-7) = 0. Это можно проиллюстрировать на числовой прямой, где положительные числа находятся справа от нуля, а отрицательные числа - слева. Обратные числа располагаются симметрично относительно нуля.
Таким образом, понимание и использование обратных данных является важным элементом в изучении математики. Оно помогает решать задачи, выполнять операции с числами и находить решения уравнений. Знание правил обратных данных позволяет уверенно справляться с математическими заданиями и развивать навыки логического мышления.
Что такое обратные данные?
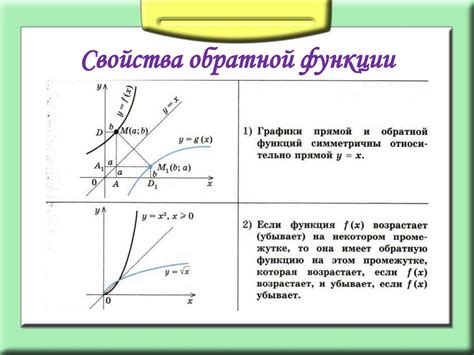
Для получения обратных данных необходимо поменять местами цифры в числе, сохраняя их порядок. Например, обратными данными числа 123 будут числа 321 и 231.
Обратные данные могут быть использованы в математике для решения задач, а также в других науках, где требуется анализ чисел и их свойств.
Обратные данные являются важным понятием в мире математики и имеют широкий спектр применений.
Обратные данные: основные понятия
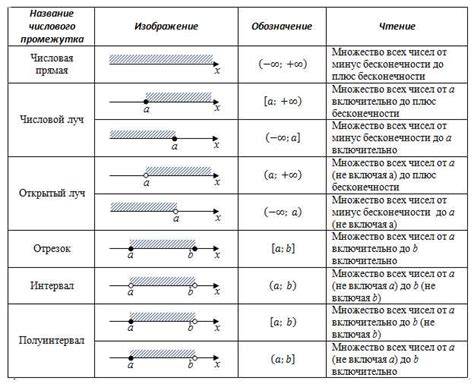
Основное правило обратных данных заключается в том, что произведение исходных данных на обратные данные всегда равно единице. То есть, если у нас есть число a и его обратное значение a-1, то a * a-1 = 1.
Обратные данные являются важными в математике и находят применение в различных областях, включая алгебру, геометрию, физику и экономику.
| Число | Обратное значение |
|---|---|
| 2 | 0.5 |
| 3 | 0.333 |
| 4 | 0.25 |
Таблица приводит примеры исходных чисел и их обратных значений. Можно заметить, что произведение каждого исходного числа на его обратное значение равно единице.
Зачем нужны обратные данные во 2 классе?

Понимание обратных данных позволяет ученикам осознать, что существует противоположное значение для каждой математической операции. Например, обратное число для суммы - это разность, обратное число для произведения - это деление.
Знание обратных данных помогает детям легче решать задачи, особенно задачи с пропущенными значениями. Они могут использовать обратные данные, чтобы найти недостающее число в уравнении и получить правильный ответ.
Также, обратные данные облегчают ученикам работу с отрицательными числами. Они могут использовать обратные значения, чтобы распознать их и выполнять операции с отрицательными числами.
Изучение и понимание обратных данных помогает детям развивать математическую интуицию и гибкость мышления. Они могут легче анализировать и решать сложные задачи, применять разные стратегии и находить различные подходы к решению проблем.
Таким образом, обратные данные являются важным инструментом для развития математических навыков учеников 2 класса. Они помогают сформировать понимание основных понятий и правил математики, а также развивают логическое мышление и гибкость ума.
Как работать с обратными данными?

Для работы с обратными данными сначала нужно понять задачу и выделить из нее ключевые понятия и условия. Затем необходимо использовать соответствующие математические операции и правила, чтобы выразить неизвестное значение через известные величины.
Основная задача работы с обратными данными состоит в том, чтобы правильно составить и решить уравнение или систему уравнений, которые позволят найти неизвестное значение. Например, если необходимо найти число, зная его сумму с другим числом и разность с третьим числом, можно записать уравнение и решить его.
При решении задач с обратными данными важно провести проверку полученного ответа, чтобы убедиться в его правильности. Проверка может быть выполнена посредством подстановки найденного значения в условие задачи и проверки его согласованности с известными данными.
Работа с обратными данными развивает логическое и абстрактное мышление, способствует формированию навыков анализа и решения проблем. Освоение этого навыка позволяет успешно решать различные задачи и применять математические знания в реальной жизни.
Какие правила существуют для обратных данных?
Основные правила для работы с обратными данными:
- При сложении двух обратных чисел нужно складывать цифры справа налево. Если получается перенос, он должен быть учтен при сложении следующих цифр.
- При вычитании обратных чисел нужно вычитать цифры справа налево. Если в процессе вычитания возникает заем, он должен быть учтен при вычитании следующих цифр.
- При умножении обратных чисел нужно перемножать цифры справа налево. Если в процессе умножения возникает перенос, он должен быть учтен при умножении следующих цифр.
- При делении обратных чисел нужно делить цифры справа налево. Если в процессе деления возникает перенос, он должен быть учтен при делении следующих цифр. В случае неправильного расчета, возникающие остатки нужно корректно отразить в ответе.
- При использовании обратных данных в математическом выражении необходимо правильно определить порядок операций и правильно расставить скобки, чтобы избежать ошибок и получить корректный результат.
С помощью этих правил можно выполнять различные арифметические операции с обратными данными и получать правильные ответы.
Примеры использования обратных данных
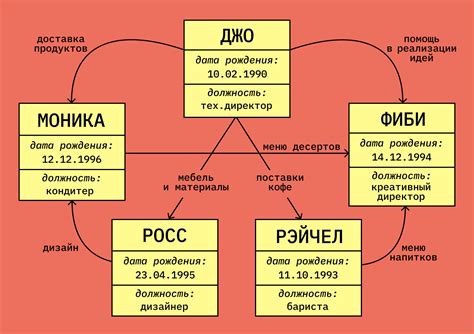
Обратные данные представляют собой специальный тип задач, где известны результаты действия и необходимо найти исходные данные или условия. Вот несколько примеров использования обратных данных в математике:
- Задача на нахождение числа: известно, что результат умножения двух чисел равен 15, а одно из чисел равно 5. Необходимо найти второе число. Решение: делаем обратную операцию – делим известный результат на известное число: 15 ÷ 5 = 3. Таким образом, второе число равно 3.
- Задача на нахождение недостающего слагаемого: известно, что сумма двух чисел равна 10, а одно из чисел равно 3. Необходимо найти второе число. Решение: делаем обратную операцию – от известной суммы вычитаем известное число: 10 - 3 = 7. Таким образом, второе число равно 7.
- Задача на нахождение стоимости единицы товара: известно, что общая стоимость 5 одинаковых товаров составляет 100 рублей. Необходимо найти стоимость одной единицы товара. Решение: делаем обратную операцию – делим общую стоимость на количество товаров: 100 ÷ 5 = 20. Таким образом, стоимость одной единицы товара равна 20 рублей.
Обратные данные помогают ученикам развивать логическое мышление, аналитические и решательные навыки. Они также широко применяются в реальной жизни, например, при решении экономических задач, задач бюджетирования, планирования и др.
Обратные данные в математике: плюсы и минусы

Одним из главных плюсов использования обратных данных является возможность прогнозирования и предсказания будущих событий. На основе имеющихся данных мы можем построить модели и предсказать развитие процессов в будущем. Это особенно полезно в экономике, финансовой сфере и при решении задач бизнес-аналитики.
Еще одним плюсом использования обратных данных является возможность выявления закономерностей и зависимостей между различными переменными. Анализ данных позволяет нам установить, какие факторы оказывают влияние на исследуемый процесс, и способствует лучшему пониманию объекта исследования.
Во-вторых, использование обратных данных может вызвать проблемы с приватностью и безопасностью. В некоторых случаях, доступ к конфиденциальным данным может быть ограничен или запрещен политикой организации или законодательством.
Таким образом, использование обратных данных в математике имеет свои плюсы и минусы. Правильное использование данных позволяет нам делать точные прогнозы и получать новые знания, однако, необходимо учитывать потенциальные проблемы и риски, связанные с их использованием.
Как использовать обратные данные при решении задач?
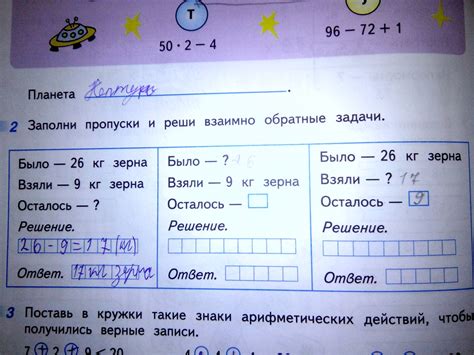
Когда решаем задачу, мы получаем определенный результат, который можно сравнить с обратными данными. Если наши ответы совпадают, значит, мы правильно решили задачу. Если же ответы отличаются, необходимо найти ошибку в решении и исправить ее.
Чтобы использовать обратные данные, необходимо внимательно прочитать условие задачи, определить, какую информацию нужно найти, и в какой форме даны обратные данные. Затем, после выполнения решения, сравнить его результат с обратными данными.
Например, если задача требует найти периметр прямоугольника, обратные данные могут предоставить правильный ответ, с которым мы сравниваем наш результат. Если ответы совпадают, значит, мы верно нашли периметр. Если ответы отличаются, нужно перепроверить решение и найти ошибку.
Также, обратные данные могут использоваться для проверки работы с формулами, правильности использования математических операций, и корректного применения правил.
Использование обратных данных позволяет нам контролировать правильность наших решений и избегать ошибок. Этот подход является важным при обучении математике и помогает улучшить навыки решения задач.
Важно помнить, что обратные данные должны быть корректными и соответствовать условию задачи. Также, необходимо учитывать возможность наличия нескольких правильных ответов или разных способов решения задачи.
Использование обратных данных - это эффективный способ проверки и контроля при решении задач. Правильное использование этого подхода позволяет улучшить качество своих решений и развить математические навыки.



