Область определения функции - это множество всех допустимых значений аргумента, при которых функция имеет смысл. Она определяет, на каких значениях можно использовать функцию и получить корректный результат.
В 10 классе область определения функции является одной из ключевых понятий в изучении математики. Она позволяет определить, на каком промежутке или в каком множестве аргументов функция существует и является определенной.
Область определения функции может быть ограничена самим аргументом или другими математическими условиями. Например, если функция содержит подкоренное выражение, то область определения будет ограничена такими значениями аргумента, при которых подкоренное выражение неотрицательно.
Важно учитывать, что область определения может быть разной для разных типов функций. Например, для линейной функции область определения - это вся числовая прямая, тогда как для рациональной функции область определения может быть ограничена значениями аргумента, при которых знаменатель не равен нулю.
Таким образом, знание области определения функции в 10 классе является неотъемлемой частью изучения математического анализа и служит основой для дальнейшего построения графиков функций, решения уравнений и прочих математических операций.
Область определения функции
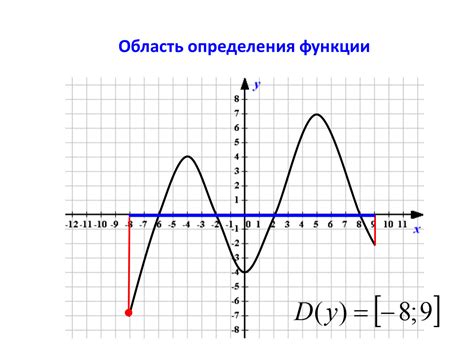
Область определения функции можно представить в виде множества чисел или интервалов на числовой прямой. В некоторых случаях область определения может быть бесконечной, а в других случаях может быть ограничена конкретными значениями.
Для определения области определения функции необходимо учитывать следующие условия:
| Тип функции | Условия для определения области определения |
|---|---|
| Полиномы | Область определения может быть всем множеством действительных чисел, так как полиномы определены для любых значений переменной. |
| Рациональные функции | Область определения рациональной функции определяется ограничениями на переменные в знаменателе функции. Значения переменной, при которых знаменатель равен нулю, исключаются из области определения. |
| Иррациональные функции | Область определения иррациональной функции определяется ограничениями, связанными с корнями и знаками внутри функции. Значения переменной, при которых корень или знак внутри функции не определены, исключаются из области определения. |
| Тригонометрические функции | Область определения тригонометрической функции может быть ограничена конкретными значениями переменной, так как некоторые значения могут привести к неопределенности или делению на ноль. |
Важно учитывать, что область определения функции представляет только те значения переменной, при которых функция имеет смысл. Значения, выходящие за пределы области определения, не могут быть использованы в вычислениях и не имеют смысла в контексте функции.
Что такое область определения

Для математических функций в 10 классе, область определения может ограничиваться различными условиями, например:
- Уравнениями, которые определяют значения переменных;
- Ограничениями на входные значения, такими как неравенства или условия на множества значений функций, например, отрицательные числа или вещественные числа;
- Ограничениями, заданными графически, например, график параболы может иметь определенную область определения, ограниченную промежутком значений х.
Область определения имеет важное значение при работе с функциями, поскольку функция не может быть определена при значениях х, которые не принадлежат ее области определения. При решении уравнений и задач с использованием функций, необходимо учитывать их область определения, чтобы исключить неправильные значения переменных и предотвратить ошибки в результатах.
Как определить область определения

Для определения области определения функции необходимо учитывать два фактора: область значений функции и возможные ограничения или исключения для независимой переменной.
В начале определения области определения следует определить область значений функции. Область значений функции представляет собой множество всех возможных значений зависимой переменной функции. Зная область значений, можно определить, для каких значений независимой переменной функция имеет смысл.
Следующий шаг – определение возможных ограничений или исключений для независимой переменной. Ограничения или исключения могут возникать вследствие математических операций, определенных в функции. Например, функция может содержать деление на ноль, что приводит к исключению значения независимой переменной, при котором это происходит.
После определения области значений функции и учета ограничений или исключений для независимой переменной, можно определить область определения, объединив множество всех значений независимой переменной с учетом данных о области значений.
Важно помнить, что область определения может быть действительным числом или иметь специальные условия и ограничения в зависимости от функции и контекста задачи.
Область определения элементарных функций

Линейная функция, заданная формулой y = ax + b, имеет область определения всю числовую прямую (-∞; +∞), так как при любом значении x функция определена.
Квадратная функция, заданная формулой y = ax^2 + bx + c, имеет область определения также всю числовую прямую (-∞; +∞), так как квадратный корень (sqrt) определен при любом значении аргумента.
Степенная функция с положительным основанием, заданная формулой y = a^x, имеет область определения (-∞; +∞). Однако, ее значения применительно к 10 классу могут быть не определены при отрицательных значениях аргумента, так как для этого нужно знание и применение понятия "комплексных чисел".
Тригонометрические функции, такие как синус, косинус, тангенс и другие, имеют область определения всю числовую прямую (-∞; +∞). Однако, значения этих функций могут быть неопределены при определенных значениях аргумента, например, при делении на ноль (например, тангенс, косеканс, котангенс при аргументах кратных π/2) или при нахождении арксинуса и арккосинуса за пределами отрезка [-1; 1].
В целом, область определения элементарных функций в 10 классе включает все значения аргумента, при которых функция может быть вычислена без использования понятия комплексных чисел или других более сложных математических концепций.
Определение области определения функции очень важно при анализе графиков функций и решении уравнений, так как оно определяет допустимость значений аргумента и помогает избегать ошибок и парадоксов в математических выкладках.
Область определения сложной функции

Область определения функции, представленной в виде сложной функции, определяется с учетом определения каждой из составляющих функций и условий, наложенных на входные значения.
Для начала, необходимо определить область определения каждой функции, входящей в сложную функцию. Для этого необходимо учитывать такие факторы, как корни, знаменатели и аргументы функций. В случае, когда одна из функций не определена в какой-то точке, область определения всей функции также будет ограничена.
При подборе значений для аргументов сложной функции необходимо учитывать условия, наложенные на входные значения функций. Например, если функция имеет знаменатель, то необходимо исключить из области определения те значения, которые приводят к делению на ноль.
Таким образом, область определения сложной функции будет состоять из тех значений, которые находятся в области определения каждой функции, входящей в сложную функцию, и удовлетворяют условиям, наложенным на входные значения.
Примеры определения области определения

Область определения функции задает множество значений аргументов, для которых функция будет иметь смысл и не будет приводить к неопределенности или ошибке.
Рассмотрим несколько примеров определения области определения функций:
1. Линейная функция:
Функция вида f(x) = kx + b, где k и b - константы.
Область определения такой функции неограниченна и задается всеми действительными числами.
2. Корень квадратный:
Функция вида f(x) = √x, где x >= 0.
Область определения такой функции ограничена положительными числами или нулем, так как корень квадратный отрицательного числа не имеет смысла в рамках вещественных чисел.
3. Обратная функция:
Функция вида f(x) = 1/x, где x ≠ 0.
Область определения такой функции исключает только значение 0, так как деление на ноль не имеет смысла и приводит к неопределенности.
В каждом конкретном случае определения области определения функции влияют на то, какие значения можно подставлять в функцию, чтобы получить корректный результат. При решении задач и построении графиков важно учитывать область определения функции.
Применение области определения при решении уравнений

Область определения функции играет важную роль при решении уравнений, так как определяет значения переменных, для которых функция имеет смысл и может быть вычислена.
При решении уравнений, необходимо учитывать, что значения переменных не могут находиться вне области определения функции. Если значение переменной находится вне области определения, то оно не является решением уравнения.
Например, если функция имеет область определения D = (-∞, 5) ∪ (5, +∞), то все значения переменной, которые меньше 5 или больше 5, не попадают в область определения и не являются решением уравнения.
При решении уравнений, необходимо также проверять полученные значения, чтобы исключить ситуации, когда значения переменных приводят к делению на ноль или вычислению корней из отрицательных чисел, что нарушает область определения функции и делает решение некорректным.
Таким образом, знание области определения функции помогает корректно решать уравнения, исключая недопустимые значения переменных и учитывая особенности функции.
Задачи из учебников

Изучение функций в 10 классе математики часто сопровождается решением задач различной сложности. Задачи из учебников помогают ученикам применить полученные знания на практике, а также развивают их логическое мышление и умение находить решения.
Примеры задач могут включать в себя построение графика функции, определение области определения функции, нахождение значения функции по заданной переменной или построение уравнения функции по заданным условиям.
Часто учебники предлагают задания, в которых нужно составить уравнение функции по графику, провести анализ функции на монотонность или экстремумы, а также найти обратную функцию.
Решение задач требует от ученика применения знаний о графиках функций, алгебре, аналитической геометрии и математическом анализе. Также, задачи могут быть связаны с другими разделами математики, например, с геометрией или статистикой.
Решение задач помогает ученикам не только применить теоретические знания на практике, но и развить их креативное и критическое мышление. Задачи из учебников дают ученикам возможность самостоятельно исследовать материал, анализировать и обобщать информацию, а также находить различные подходы к решению задач.
В целом, задачи из учебников помогают ученикам углубить свое понимание функций, области их определения и обратных функций, а также развить навыки аналитического мышления и решения математических задач.



