В 11 классе школьной программы по математике одной из важных тем является область изменения функции. Это понятие играет важную роль в анализе функций и позволяет определить, на каком промежутке аргументы функции могут принимать значения. Умение определять область изменения функции является необходимым для решения множества задач и оптимизации процессов в различных областях науки и техники.
Область изменения функции определяется ограничениями на значения аргументов функции. В математике область изменения функции может быть задана в явном виде или вычислена на основе свойств самой функции. Например, для функции вида f(x) = x^2, область изменения будет всем множеством действительных чисел, так как значение функции может быть любым. Однако, в случае функции вида f(x) = 1/x, область изменения будет исключать значение x = 0, так как деление на ноль невозможно.
Для определения области изменения функции необходимо учитывать различные ограничения. Например, функция может содержать радикал, и в этом случае необходимо исключить значения аргумента, при которых радикал будет отрицательным. Также функция может содержать знаменатель, поэтому необходимо исключить значения аргумента, при которых знаменатель будет равен нулю.
В данной статье мы рассмотрим несколько примеров определения области изменения функций и покажем, как учитывать различные ограничения. Понимание области изменения функции позволит лучше понять ее свойства и использовать ее в различных математических задачах.
Понятие области изменения функции
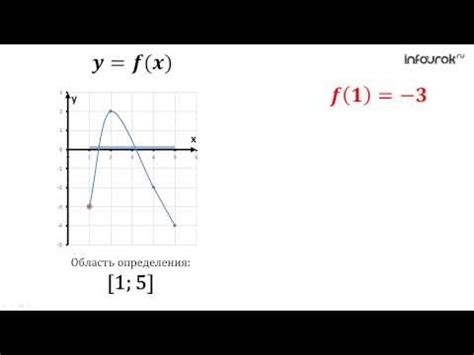
Для того чтобы понять понятие области изменения функции, рассмотрим пример. Допустим, у нас есть функция f(x) = x^2, где x - независимая переменная, а f(x) - зависимая переменная. Подставив вместо x различные значения, мы можем получить значения f(x).
| x | f(x) |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Из таблицы видно, что функция f(x) = x^2 может принимать значения 4, 1 и 0 в зависимости от значения x. Таким образом, область изменения функции f(x) = x^2 равна множеству {0, 1, 4}.
Область изменения функции может быть ограничена или неограничена. Если функция имеет нижнюю или верхнюю границу для своих значений, то область изменения будет ограниченной. Например, функция f(x) = sin(x) ограничена значением от -1 до 1.
Важно понимать область изменения функции, так как она помогает определить множество значений, которые может принимать функция и помогает в анализе поведения функции на заданном интервале.
Как определить область изменения функции

Область изменения функции определяет множество значений, которое может принимать аргументы функции. Для того чтобы определить область изменения функции, необходимо учитывать различные факторы.
Во-первых, необходимо принять во внимание определитель наличия знаменателя или корня в функции. Если функция содержит знаменатель, то его значение не может быть равно нулю, поэтому нужно исключить значения аргументов, при которых знаменатель обращается в ноль. Аналогично, если функция содержит корень, то значение подкоренного выражения должно быть неотрицательным, поэтому нужно исключить значения аргументов, при которых подкоренное выражение отрицательное.
Во-вторых, необходимо учитывать определитель принадлежности определенной области данных. Например, если функция определена на множестве действительных чисел, то область изменения функции будет множество всех действительных чисел. Однако, если функция определена только на множестве натуральных чисел, то область изменения функции будет множество всех натуральных чисел. Таким образом, чтобы определить область изменения функции, нужно знать, на каком множестве определена сама функция.
Кроме того, необходимо учитывать предельные значения аргументов функции. Например, если функция имеет асимптоту, то область изменения функции будет множество всех значений аргументов, кроме точек, в которых функция не определена или не существует.
Наконец, важно учитывать возможные ограничения на значения аргументов, которые могут быть заданы в условии задачи или поставлены исходя из контекста. Например, если говорится, что аргумент функции должен быть положительным числом, то необходимо исключить значения аргументов, которые могут быть отрицательными.
Таким образом, для определения области изменения функции необходимо учитывать наличие знаменателя или корня, принадлежность определенной области данных, предельные значения аргументов и возможные ограничения на значения аргументов. И только учитывая все эти факторы, можно определить область изменения функции.
Одномерная область изменения функции

Например, рассмотрим функцию f(x) = x^2. Ее одномерная область изменения может быть задана интервалом (-∞, +∞), так как функция определена и изменяется на всей числовой прямой.
Однако, существуют и другие функции, у которых одномерная область изменения может быть ограничена. Например, функция g(x) = √x определена только на интервале [0, +∞), так как квадратный корень из отрицательного числа не существует.
| Функция | Одномерная область изменения |
|---|---|
| f(x) = x^2 | (-∞, +∞) |
| g(x) = √x | [0, +∞) |
Также, одномерная область изменения функции может быть задана числовыми значениями, если функция не изменяется на определенном промежутке. Например, функция h(x) = 10 не изменяется для любого значения x, и ее одномерная область изменения будет равна {10}.
Понимание одномерной области изменения функции важно при анализе ее свойств, поиске корней, нахождении непрерывного интервала значений и многих других математических операций.
Двумерная область изменения функции
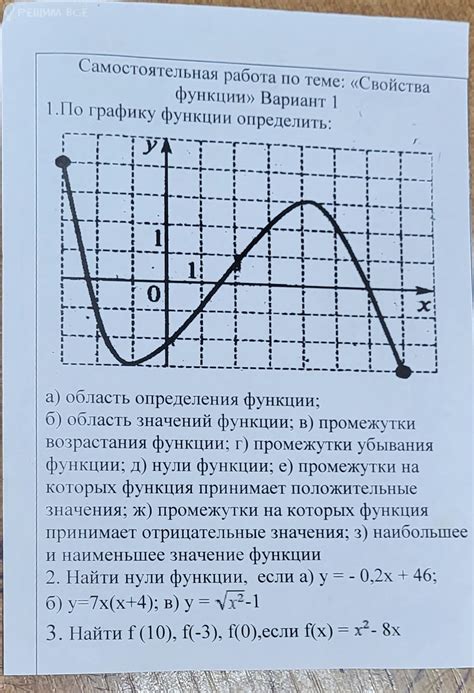
Область изменения функции – это множество значений, которые может принимать функция на своей области определения. В случае двумерной функции, областью определения является множество точек в двумерной системе координат, а область изменения – множество значений функции на этой области определения.
Для того чтобы определить область изменения функции, нужно анализировать ее график на двумерной плоскости. На графике функции будут отображены все точки, которые принимает функция на своей области определения.
Важно понимать, что функция может принимать различные значения на своей области определения. Например, функция может быть ограничена таким образом, что ее область изменения будет ограничена между двумя значениями, или функция может принимать все возможные значения в заданном диапазоне.
Рассмотрим пример функции y = x^2, которая является частным случаем параболы. График этой функции -- парабола с вершиной в начале координат и открывается вверх. Область определения этой функции -- все действительные числа, а область изменения -- все неотрицательные числа.
Таким образом, двумерная область изменения функции будет отображать все возможные значения функции на двумерной плоскости внутри выбранного диапазона.
Примеры задач на определение области изменения функции
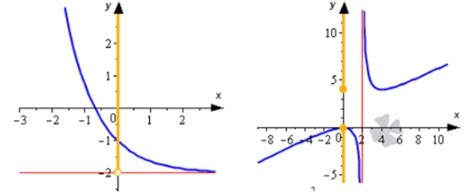
Пример 1:
Определить область изменения функции f(x) = x^2 - 4 при заданном условии x ≥ 0.
Для решения задачи необходимо определить значения функции f(x) при x ≥ 0.
Область изменения функции f(x) = x^2 - 4 при x ≥ 0 будет равна множеству всех неотрицательных чисел и нуля: D = x .
Пример 2:
Определить область изменения функции g(x) = 5 - |x| при заданном условии -2 ≤ x ≤ 3.
Для решения задачи необходимо определить значения функции g(x) при -2 ≤ x ≤ 3.
Область изменения функции g(x) = 5 - |x| при -2 ≤ x ≤ 3 будет равна множеству всех чисел от 2 до 3 включительно: D = -2 ≤ x ≤ 3.
Пример 3:
Определить область изменения функции h(x) = √(x + 4) при заданном условии x + 4 ≥ 0.
Для решения задачи необходимо определить значения функции h(x) при x + 4 ≥ 0.
Так как корень квадратный из неотрицательного числа всегда существует, то область изменения функции h(x) = √(x + 4) при x + 4 ≥ 0 будет равна множеству всех чисел, для которых выполняется условие x + 4 ≥ 0: D = x ≥ -4.
Определение области изменения функции – это важный этап анализа функций. Правильное определение области изменения функции позволяет более точно описать ее поведение и использовать полученную информацию для решения задач и построения графиков функций.



