Треугольник в окружности – геометрическая фигура, в которой все вершины треугольника лежат на окружности. Изучение площади такого треугольника является важной задачей в геометрии. В данной статье мы рассмотрим, как вычислить площадь треугольника, построенного внутри окружности.
Существует несколько способов определения площади треугольника в окружности, но один из наиболее простых – использование формулы для вычисления площади треугольника по его сторонам. Если известны все стороны треугольника в окружности, то можно использовать формулу Герона для вычисления площади.
Формула Герона:
S = sqrt(p * (p - a) * (p - b) * (p - c)),
где S – площадь треугольника, a, b, c – длины сторон треугольника, p – полупериметр треугольника, равный сумме длин сторон, деленной на 2.
Вычислить площадь треугольника в окружности может быть полезно в различных сферах, таких как архитектура, инженерное дело и геодезия. Знание этой формулы позволяет удобно и быстро рассчитывать площадь треугольника, имея информацию о его сторонах, что делает ее отличным инструментом для решения геометрических задач.
Что такое площадь треугольника?
Для вычисления площади треугольника можно использовать различные методы, в зависимости от доступной информации о треугольнике. Один из наиболее распространенных методов - формула Герона, которая основана на знании длин всех сторон треугольника.
Формула Герона выглядит следующим образом:
- Пусть a, b и c - длины сторон треугольника.
- Полупериметр треугольника p равен сумме длин всех сторон, деленной на 2: p = (a + b + c) / 2.
- Площадь треугольника S вычисляется по формуле: S = √(p * (p - a) * (p - b) * (p - c)).
Таким образом, площадь треугольника зависит от длин его сторон и может быть вычислена с использованием формулы Герона или других методов, если известны дополнительные параметры треугольника, например, высота или радиус вписанной окружности.
Определение и формула
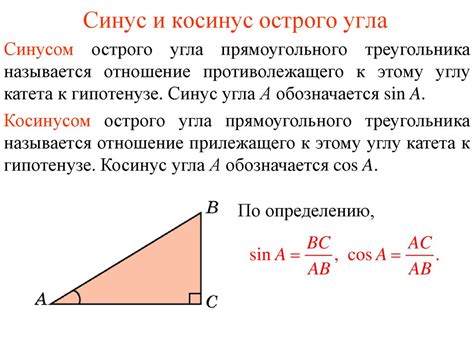
Формула для вычисления площади треугольника, вписанного в окружность, имеет вид:
S = r * p
где S - площадь треугольника, r - радиус вписанной окружности, а p - полупериметр треугольника.
Связь площади треугольника с радиусом окружности

Площадь треугольника, вписанного в окружность, имеет прямую связь с радиусом окружности. Для вычисления площади треугольника, необходимо учитывать радиус окружности, в которую треугольник вписан.
Радиус окружности является отрезком от центра окружности до любой точки на ее окружности. Если треугольник вписан в окружность, то каждая сторона треугольника является хордой, проходящей через центр окружности.
Площадь треугольника в окружности можно вычислить с помощью следующей формулы:
S = (1/2) * a * b * sin(C)
Где:
- S - площадь треугольника
- a и b - длины сторон треугольника
- C - угол между сторонами a и b
Радиус окружности можно выразить через длины сторон треугольника с помощью формулы:
R = (a * b * c) / (4 * S)
Где:
- R - радиус окружности
- c - третья сторона треугольника
Используя эти формулы, можно вычислить площадь треугольника, зная радиус окружности. Также можно выразить радиус окружности через длины сторон треугольника и площадь.
Связь площади треугольника с радиусом окружности позволяет нам использовать радиус для нахождения площади треугольника и наоборот, что является полезным при решении задач в геометрии и строительстве.
Примеры расчетов площади треугольника в окружности
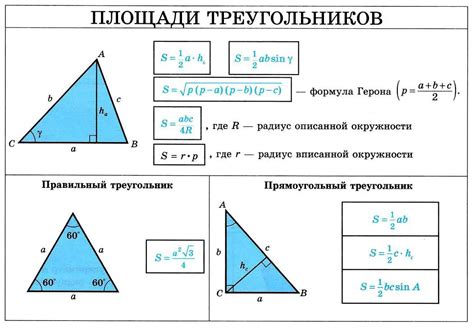
Для расчета площади треугольника в окружности, необходимо знать длины сторон треугольника и радиус окружности, в которую он вписан.
Предположим, у нас есть треугольник ABC, вписанный в окружность радиусом r.
Длина сторон треугольника: AB = a, BC = b, AC = c.
Сумма длин любых двух отрезков, образующих треугольник, равна длине третьего отрезка. То есть AB + BC = AC, AB + AC = BC, BC + AC = AB.
Также известно, что любой угол, образованный лучами, исходящими из центра окружности и точки пересечения с окружностью, равен половине центрального угла, опирающегося на эту дугу.
Площадь треугольника в окружности можно вычислить по формуле:
S = (1/2) * a * b * c / (4 * r)
Рассмотрим пример:
Пусть AB = 6, BC = 8, AC = 10, r = 5. Применим формулу:
S = (1/2) * 6 * 8 * 10 / (4 * 5) = 24
Таким образом, площадь треугольника ABC, вписанного в окружность радиусом 5, равна 24.



