Когда мы говорим о числах, одно из первых понятий, которое приходит на ум, это натуральные числа. Но что такое натуральные числа и в чем их особенности?
Натуральные числа - это целые положительные числа, начиная от единицы и бесконечно продолжающиеся вправо по числовой прямой. Они служат основой для построения всей системы чисел и являются наиболее естественным и интуитивным представлением количества.
Какими же особенностями обладают натуральные числа? Во-первых, они позволяют нам совершать простейшие арифметические операции: сложение, вычитание, умножение и деление. Они также образуют бесконечную последовательность, в которой каждое следующее число больше предыдущего.
Натуральные числа имеют большое значение не только в математике, но и во многих других областях науки и жизни человека. Они используются для подсчета, измерения, классификации и описания явлений окружающего мира. Без натуральных чисел было бы сложно представить себе нашу повседневную жизнь, поскольку они описывают все вокруг нас, начиная от количества людей в помещении до количество наносекунд в цикле процессора.
Что такое натуральные числа?

Натуральные числа можно представить в виде упорядоченной последовательности чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...
Каждое следующее число в этой последовательности на единицу больше предыдущего.
Натуральные числа играют важную роль в математике, их используют для счета, измерения и решения различных задач. Они широко применяются в науке, технике, экономике и других областях человеческой деятельности.
Натуральные числа также имеют некоторые особенности:
- Неограниченность: натуральные числа не имеют верхней границы и могут продолжаться бесконечно.
- Сложение и умножение: натуральные числа можно складывать и умножать между собой, получая другие натуральные числа.
- Упорядоченность: натуральные числа расположены в порядке возрастания, что позволяет выполнять сравнения и определять, какое число больше или меньше другого.
Натуральные числа являются основой для формирования других классов чисел, таких как целые, рациональные, иррациональные и дробные числа.
Определение натуральных чисел
Натуральные числа символизируются с помощью буквы N и являются одним из основных типов чисел в математике. Они позволяют считать и классифицировать объекты в различных областях знаний, от более простых, таких как количество яблок в корзине до более сложных, таких как число атомов в молекуле или количество часов, прошедших с начала дня.
Важно отметить, что натуральные числа не включают отрицательные числа, десятичные дроби или нуль, поэтому они не могут использоваться для представления отрицательных или нецелых величин.
Какие числа входят в натуральные числа?

Натуральные числа обозначаются символом N и могут быть представлены в виде бесконечной последовательности: 1, 2, 3, 4, 5, ...
Особенностью натуральных чисел является то, что они не содержат нуля и отрицательных чисел. Например, -1, -2, 0 не являются натуральными числами.
Натуральные числа можно упорядочить по возрастанию, и между любыми двумя натуральными числами всегда можно найти другое натуральное число.
Натуральные числа широко применяются в математике, науке, экономике и повседневной жизни для решения различных задач и измерений. Они формируют основу для более сложных числовых систем и концепций, таких как целые числа, рациональные числа и действительные числа.
В целом, натуральные числа являются базовым и важным математическим понятием, которое помогает нам понять и описать мир вокруг нас и его числовую структуру.
Как выразить натуральные числа в виде алгебраических выражений?

Натуральные числа могут быть выражены в виде алгебраических выражений с использованием различных математических операций.
Одним из способов выражения натуральных чисел является использование основных арифметических операций, таких как сложение, вычитание, умножение и деление. Например, число 5 может быть выражено как сумма 2+3 или произведение 1*5.
Другим способом представления натуральных чисел является использование степеней. Например, число 2 может быть выражено в виде 2^1, а число 3 - в виде 2^1 + 1.
Также можно использовать квадратные корни для выражения натуральных чисел. Например, число 4 может быть выражено в виде √16, а число 9 - как √81.
Степени и квадратные корни могут быть использованы вместе с основными арифметическими операциями для более сложных выражений. Например, число 10 может быть выражено как 2^3 + 2*2.
Эти примеры показывают лишь небольшую часть возможностей выражения натуральных чисел в виде алгебраических выражений. Знание основных математических операций и правил алгебры позволяет строить более сложные выражения для любого натурального числа.
| Натуральное число | Алгебраическое выражение |
|---|---|
| 1 | 1 |
| 2 | 2^1 |
| 3 | 2^1 + 1 |
| 4 | √16 |
| 5 | 2+3 |
| 6 | 2*3 |
| 7 | 2^2 + 3 |
| 8 | 2^3 |
| 9 | √81 |
| 10 | 2^3 + 2*2 |
Натуральные числа могут быть выражены в виде алгебраических выражений, используя различные комбинации математических операций. Это позволяет более гибко и точно описывать числа и их свойства в математических вычислениях.
Особенности натуральных чисел
Особенности натуральных чисел:
| Свойство | Описание |
| Порядок | Натуральные числа имеют строго определенный порядок, начиная с единицы и последовательно увеличиваясь на единицу. |
| Бесконечность | Натуральные числа не имеют верхней границы и могут продолжаться бесконечно. |
| Отсутствие дробей и отрицательных значений | Натуральные числа являются целыми положительными числами и не могут быть дробными или отрицательными. |
| Использование в счете | Натуральные числа используются для подсчета количества предметов или явлений и в нумерации, например 1 яблоко, 2 стола и т.д. |
Эти особенности делают натуральные числа важными и неотъемлемыми элементами математического аппарата и повседневной жизни.
Натуральные числа и их применение в математике

Натуральные числа имеют широкое применение в различных областях математики. Они используются в арифметике для выполнения основных операций, таких как сложение, вычитание, умножение и деление. Натуральные числа также играют важную роль в теории чисел, алгебре, геометрии и других разделах математики.
В теории чисел, натуральные числа являются основным объектом изучения. Они используются для определения различных классов чисел, таких как простые числа, составные числа, перевернутые числа и т. д. Натуральные числа также используются для формулирования и доказательства теорем и законов, которые описывают различные свойства числовых последовательностей и алгебраических структур.
В геометрии натуральные числа используются для определения и измерения различных геометрических объектов, таких как длины, площади, объемы и т. д. Натуральные числа также используются для формулирования и доказательства геометрических теорем и законов.
Одно из важных свойств натуральных чисел - их возрастающая последовательность. Каждое следующее натуральное число больше предыдущего на единицу. Это свойство позволяет использовать натуральные числа для счета и упорядочения объектов.
Как складывать натуральные числа?

Пример:
56
+ 27
---------
11
В данном примере, сначала сложились единицы: 6 + 7 = 13. Так как получилось число больше 9, перенесли единицу на следующий разряд. Затем сложились десятки: 5 + 2 + 1 = 8. Итоговый результат: 83.
Сложение натуральных чисел можно выполнять не только в столбик, но и в строку. Для этого нужно сложить числа слева направо, а переносы обрабатывать справа налево.
Как умножать натуральные числа?

Умножение натуральных чисел можно представить как последовательное сложение одного числа другого число раз. Например, чтобы умножить 3 на 4, нужно три раза прибавить к числу 3 само число 4:
3 + 3 + 3 + 3 = 12
Для умножения числа на 0 используется особое правило: произведение любого числа на 0 равно 0. Например,
5 * 0 = 0
Умножение натуральных чисел также обладает рядом свойств, включая коммутативность (порядок множителей не влияет на результат), ассоциативность (порядок операций не влияет на результат) и дистрибутивность (умножение распространяется на сложение).
Важно помнить, что результат умножения двух натуральных чисел всегда будет натуральным числом, если оба множителя таковы.
Деление натуральных чисел: правила и примеры
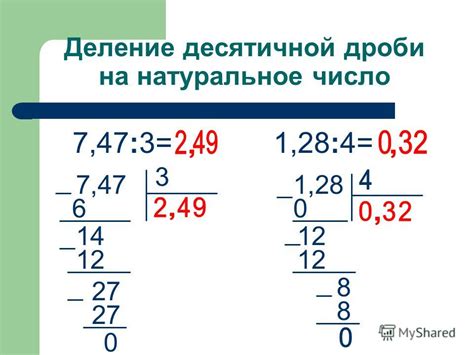
Основное правило деления натуральных чисел заключается в том, что число, на которое делится (делитель), должно быть меньше или равно делимому числу. Если делитель больше делимого, то результатом деления будет ноль.
Деление натуральных чисел можно представить в виде операции деления нацело и операции нахождения остатка от деления. Результат деления нацело будет натуральным числом, а остаток от деления будет натуральным числом, меньшим делителя.
Пример деления натуральных чисел:
Делимое: 15
Делитель: 3
15 : 3 = 5
Остаток от деления: 0
В результате деления 15 на 3 получаем частное равное 5 и остаток равный 0.



