В математике существуют различные виды чисел, каждый из которых имеет свои особенности и применение. Два наиболее распространенных вида чисел – это натуральные и целые числа. Несмотря на то, что они оба являются положительными числами, у них существуют существенные отличия.
Натуральные числа – это набор чисел, которыми мы считаем предметы в повседневной жизни: 1, 2, 3, 4 и так далее. Они начинаются с единицы и бесконечны. Натуральные числа используются для подсчета объектов или представления порядка, например, порядков номера матчей или номера товара.
В отличие от натуральных чисел, целые числа включают в себя все натуральные числа, а также их противоположности – отрицательные числа. Целые числа имеют вид ... -3, -2, -1, 0, 1, 2, 3 ... и так далее. Они используются для представления температуры, денежных потоков, координат и прочих величин, которые могут иметь как положительное, так и отрицательное значение.
Одно из свойств натуральных чисел – их упорядоченность. Натуральные числа можно упорядочить по возрастанию или по убыванию. Кроме того, натуральные числа можно складывать, вычитать, умножать и делить. Однако для натуральных чисел не определена операция вычитания, которая дает отрицательные числа. Это одно из основных отличий от целых чисел.
Отличия натуральных чисел и целых чисел
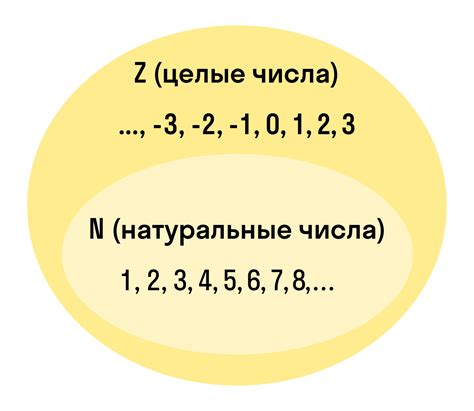
Натуральные числа могут быть использованы для подсчета предметов или для идентификации порядка в ранжировании. Они обозначаются символом N. Примеры натуральных чисел: 1, 2, 3, 4, 5 и так далее.
Целые числа - это числа, которые включают в себя натуральные числа, отрицательные числа и ноль.
В отличие от натуральных чисел, целые числа могут быть использованы для описания положительных и отрицательных направлений, отклонений, температур и других концепций. Они обозначаются символом Z. Примеры целых чисел: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 и так далее.
Таким образом, основное отличие между натуральными числами и целыми числами заключается в том, что целые числа включают в себя отрицательные числа и ноль, тогда как натуральные числа начинаются с единицы и не включают отрицательные значения.
Основные свойства натуральных чисел

Основные свойства натуральных чисел включают:
- Натуральные числа являются бесконечным множеством. Это означает, что для каждого натурального числа существует следующее натуральное число, и так далее, в бесконечность.
- У натуральных чисел есть единственный следующий элемент. То есть, если у нас есть натуральное число n, то следующее за ним натуральное число можно получить, добавив к нему единицу: n+1.
- У натуральных чисел есть единица в качестве наименьшего элемента. Это означает, что 1 - самое маленькое из всех натуральных чисел.
- Натуральные числа можно складывать, вычитать, умножать и делить. Результат этих операций также будет являться натуральным числом.
- Натуральные числа образуют возрастающую последовательность. Каждое следующее число больше предыдущего на единицу.
- У натуральных чисел есть свойство ассоциативности. Это означает, что порядок выполнения операций сложения и умножения не влияет на их результат.
Эти свойства позволяют использовать натуральные числа для счета, измерения и решения различных задач.
Основные свойства целых чисел
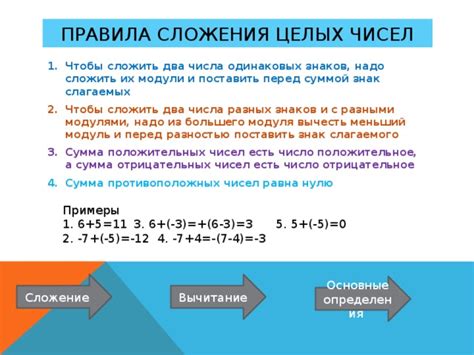
1. Замкнутость относительно сложения и вычитания:
Целые числа образуют замкнутое относительно сложения и вычитания множество. Это означает, что если сложить или вычесть два целых числа, то результат также будет целым числом.
2. Существование обратного элемента по сложению:
Для каждого целого числа a существует такое целое число, которое сложенное с a даст нуль. Это число называется обратным элементом по сложению.
3. Ассоциативность сложения и умножения:
Сложение и умножение целых чисел ассоциативны, то есть порядок, в котором производятся операции, не влияет на итоговый результат.
4. Коммутативность сложения и умножения:
Порядок, в котором складываются или перемножаются целые числа, не влияет на их сумму или произведение.
5. Существование обратного элемента по умножению (для ненулевых чисел):
Хотя для нуля обратного элемента по умножению не существует, для каждого ненулевого целого числа a существует такое целое число, которое умноженное на a даст единицу. Это число называется обратным элементом по умножению.
6. Дистрибутивность умножения относительно сложения:
Умножение целого числа на сумму двух других целых чисел равносильно умножению числа на каждое из этих чисел отдельно и сложению полученных произведений.
Важность понимания различий

Натуральные числа – это числа, которые используются для подсчета предметов или сущностей, которые можно посчитать, начиная с единицы и продолжая бесконечно: 1, 2, 3, 4, 5 и так далее. Они широко используются в теории чисел, арифметике, геометрии, а также в физике, экономике и других науках.
Целые числа, в свою очередь, включают в себя все натуральные числа и их противоположности (отрицательные числа) и нуль. Они обозначаются как: ..., -3, -2, -1, 0, 1, 2, 3, ... Целые числа также широко применяются в математике и других науках, особенно в алгебре и анализе, где они позволяют решать более сложные задачи и моделировать реальные явления.
Понимание различий между натуральными и целыми числами помогает нам более точно формулировать задачи и решать их, а также быть более гибкими в математическом мышлении. Например, в некоторых задачах нам необходимо работать только с положительными числами, в то время как в других ситуациях нам могут понадобиться отрицательные числа или ноль. Знание этих различий поможет нам выбрать правильный подход к решению каждой конкретной задачи и избежать ошибок.



