Множество истинности предложения p x – это набор всех значений, которые могут принимать переменные x и p в заданной логической системе. В других словах, множество истинности представляет собой уникальный набор комбинаций переменных, которые определяют, является ли предложение p истинным или ложным.
Множество истинности предложения p x можно представить в виде таблицы истинности, где каждая строка таблицы соответствует одной комбинации значений переменных, а столбцы представляют переменные и результат выполнения предложения p. В таблице истинности двоичной логики каждая переменная может принимать только два значения: истину (1) или ложь (0).
Множество истинности предложения p x является важным понятием в математической логике и информатике. Оно позволяет анализировать логические выражения, определять условия и правила их выполнения, а также представлять информацию в виде булевых функций. Знание о множестве истинности предложения p x помогает улучшить логическое мышление, а также разрабатывать сложные алгоритмы и программы.
Множество истинности предложения p x

Для каждого значения x существует соответствующее значение высказывания p. Если высказывание истинно при определенном значении x, то это значение входит в множество истинности. Если высказывание ложно при заданном значении x, то это значение не входит в множество истинности.
Множество истинности предложения p x может быть конечным или бесконечным, в зависимости от количества значений, которые может принимать высказывание при заданных значениях x.
Определение множества истинности предложения p x позволяет анализировать его логическую структуру и проводить логические операции, такие как конъюнкция, дизъюнкция, импликация и отрицание.
Определение множества истинности
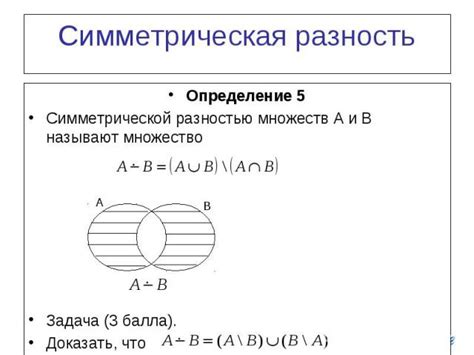
Множество истинности предложения p представляет собой совокупность всех возможных комбинаций истинности его логических переменных.
Логическое предложение может содержать одну или несколько логических переменных, которые могут принимать значения "истина" или "ложь". Множество истинности показывает, какие значения могут принимать эти переменные для каждой комбинации.
Множество истинности может быть представлено в виде таблицы истинности, где каждая строка соответствует одной комбинации переменных, а столбцы показывают значения переменных и значение самого предложения.
Например, для предложения p = "A и B" множество истинности будет содержать следующие комбинации:
- A = И, B = И, p = Истина
- A = И, B = Л, p = Ложь
- A = Л, B = И, p = Ложь
- A = Л, B = Л, p = Ложь
Множество истинности помогает определить логическую связь между переменными и их влияние на истинность предложения.
Примеры множеств истинности
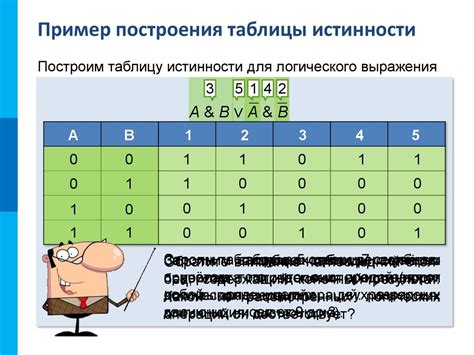
Множество истинности предложения может принимать различные значения в зависимости от значений его элементов. Рассмотрим несколько примеров:
Предложение "p и q".
- Если p = истина и q = истина, то множество истинности равно {истина};
- Если p = истина и q = ложь, то множество истинности равно {ложь};
- Если p = ложь и q = истина, то множество истинности равно {ложь};
- Если p = ложь и q = ложь, то множество истинности равно {ложь}.
Предложение "p или q".
- Если p = истина и q = истина, то множество истинности равно {истина};
- Если p = истина и q = ложь, то множество истинности равно {истина};
- Если p = ложь и q = истина, то множество истинности равно {истина};
- Если p = ложь и q = ложь, то множество истинности равно {ложь}.
Предложение "если p, то q".
- Если p = истина и q = истина, то множество истинности равно {истина};
- Если p = истина и q = ложь, то множество истинности равно {ложь};
- Если p = ложь и q = истина, то множество истинности равно {истина};
- Если p = ложь и q = ложь, то множество истинности равно {истина}.
Таким образом, множества истинности предложений могут быть различными в зависимости от значений их элементов.



