Медиана - это линия, которая соединяет вершину треугольника с серединой противоположной стороны. В равнобедренном треугольнике медиана делит основание на две равные части и перпендикулярна ему. Возможно, ты интересуешься, чему равна длина медианы в таком треугольнике. Для решения этой задачи существует простая формула.
Пусть a - длина основания равнобедренного треугольника, b - длина боковой стороны треугольника, а m - длина медианы. Тогда по формуле длина медианы вычисляется по следующей формуле:
m = √(2b2 + a2) / 2
Таким образом, чтобы найти длину медианы в равнобедренном треугольнике, необходимо знать длину его основания и боковой стороны. Подставив значения в формулу, можно получить точный ответ. Не забывай, что медиана равнобедренного треугольника также является высотой и делит основание на две равные части.
Определение равнобедренного треугольника
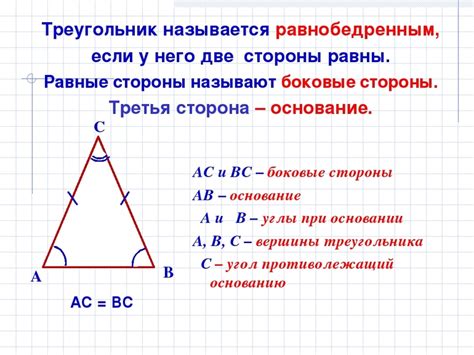
Определить равнобедренный треугольник можно использовав следующий признак: если в треугольнике две стороны равны между собой, то и два противолежащих им угла также равны. Таким образом, определить равнобедренный треугольник можно по длине его сторон либо по равенству углов.
Равнобедренные треугольники встречаются в различных областях геометрии и математики и имеют определенные свойства и формулы. Например, медиана в равнобедренном треугольнике делит основание треугольника на две равные части, а его длина может быть вычислена с использованием формулы.
Свойства равнобедренного треугольника
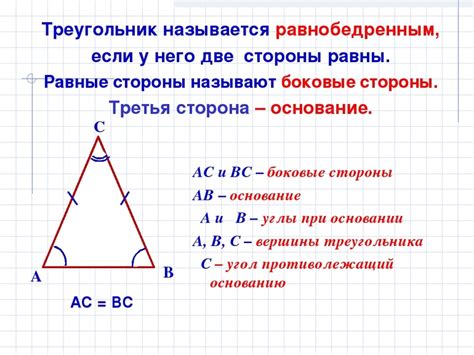
- Базы равнобедренного треугольника - это две равные стороны, на которых лежат равные углы.
- Высота равнобедренного треугольника - это отрезок, проведенный из вершины треугольника к основанию (середине базы) перпендикулярно основанию. Он делит основание на две равные части.
- Медиана равнобедренного треугольника - это отрезок, проведенный из вершины треугольника к середине противолежащей стороны (между двумя равными сторонами). Она делит треугольник на две равные площади и равна половине боковой стороны.
- Биссектриса равнобедренного треугольника - это прямая, проведенная из вершины треугольника к основанию и делающая равные углы со сторонами треугольника. Она делит угол при вершине на два равных угла.
Эти свойства помогают упростить решение задач, связанных с равнобедренными треугольниками, а также помогают лучше понять их характеристики и особенности.
Медиана в треугольнике
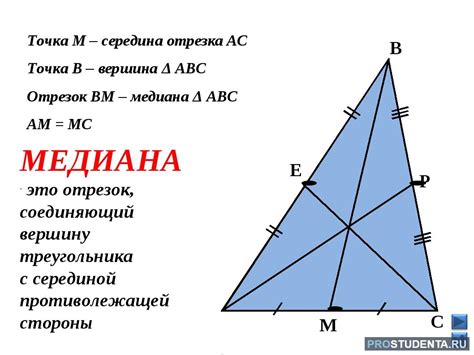
Если равнобедренный треугольник имеет стороны a, b, c, где a - основание треугольника (основание составляют две равные стороны b), то медиана m, проведенная из вершины треугольника к основанию, будет равна половине основания a:
m = a/2
Таким образом, в равнобедренном треугольнике медиана, проведенная из вершины, соответствующей основанию, равна половине основания.
Что такое медиана в равнобедренном треугольнике?
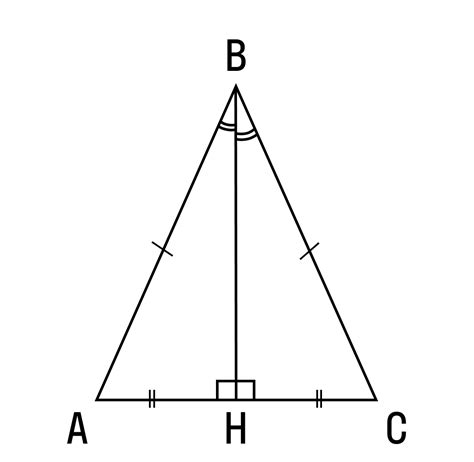
В равнобедренном треугольнике есть три медианы, которые делят треугольник на три равные части: медиана, исходящая из вершины, делит треугольник на два равных подтреугольника, а две другие медианы делят треугольник на четыре равных подтреугольника.
Соотношение длин медиан может быть найдено с использованием специальной формулы:
- Длина медианы, исходящей из вершины, равна половине биссектрисы угла при этой вершине.
- Длина двух других медиан равна половине основания треугольника.
Медианы в равнобедренном треугольнике имеют ряд интересных свойств. Например, точка пересечения всех трех медиан называется центром тяжести равнобедренного треугольника и всегда находится внутри треугольника на расстоянии, равном двум третям длины медианы.
Формула для вычисления медианы в равнобедренном треугольнике
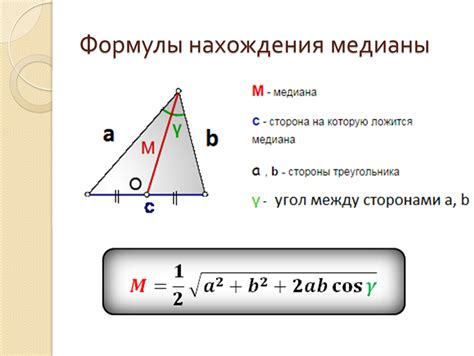
Медиана = (√2/2) * a
где a - длина основания равнобедренного треугольника.
Формула основана на свойствах равнобедренного треугольника, в котором медиана является высотой. Она делит основание на две равные части и образует прямоугольный треугольник с основанием и половиной основания.
Используя данную формулу, можно вычислить длину медианы в равнобедренном треугольнике при известной длине основания.
Примечание: в данной формуле используется значение (√2/2), которое является приближенным значением числа 0.7071.
Пример вычисления медианы в равнобедренном треугольнике
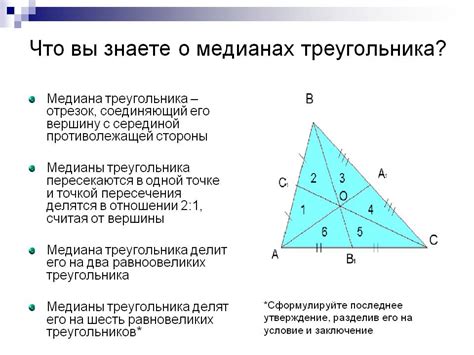
Медианы в треугольнике - это отрезки, соединяющие вершину треугольника с серединой противолежащей стороны.
Формула для вычисления медианы в равнобедренном треугольнике такая:
Медиана = √(2a² + b²)/2
Где:
- a - длина боковой стороны треугольника (основание)
- b - длина медианы
Ниже приведен пример вычисления медианы в равнобедренном треугольнике:
Пусть в равнобедренном треугольнике сторона a равна 6 см, а медиана b равна 4 см.
Подставим значения в формулу:
Медиана = √(2 * 6² + 4²)/2 = √(72 + 16)/2 = √88/2 = √44 ≈ 6.63 см
Таким образом, медиана в равнобедренном треугольнике со стороной 6 см и медианой 4 см равна примерно 6.63 см.
Интересные факты о медиане в равнобедренном треугольнике
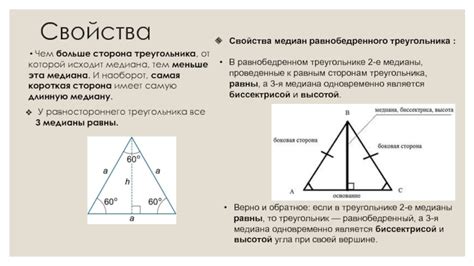
- Медиана делит основание равнобедренного треугольника пополам. Это означает, что расстояние от вершины до основания по медиане будет равно половине длины основания.
- В равнобедренном треугольнике все три медианы пересекаются в одной точке, называемой центром тяжести. Это значит, что если провести медианы из каждой вершины треугольника, они все пересекутся в одной точке.
- Медиана также является высотой и биссектрисой равнобедренного треугольника. Это означает, что она перпендикулярна основанию треугольника и делит его на две равные части.
- Длина медианы может быть вычислена по формуле:
m = \frac{\sqrt{2}}{2} \cdot a, гдеm- длина медианы,a- длина основания треугольника.
Медиана в равнобедренном треугольнике является важным элементом, который помогает определить различные параметры и свойства этого типа треугольника. Знание этих фактов может быть полезно при решении геометрических задач и применении математических формул в практических ситуациях.



