Треугольник - это многоугольник, состоящий из трех отрезков, соединяющих три точки. Одно из самых важных свойств треугольника - это его медиана. Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Доказательство того, что медиана треугольника меньше его полупериметра, основывается на простом факте - полупериметр треугольника равен сумме длин двух его сторон, деленной на два. С другой стороны, медиана треугольника делит противоположную сторону пополам.
Предположим, что медиана треугольника больше его полупериметра. В таком случае, длина медианы будет больше половины суммы длин двух сторон. Но такое предположение противоречит утверждению о том, что медиана делит противоположную сторону пополам, так как, если медиана была бы больше, то одна половина противоположной стороны оказалась бы больше, чем полупериметр.
Медиана треугольника: определение и свойства
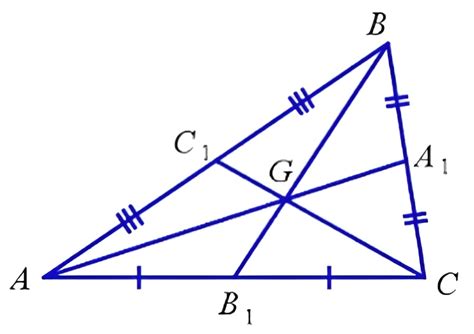
Основное свойство медианы состоит в том, что она делит сторону треугольника, к которой она проведена, пополам. Следовательно, длина медианы равна половине длины соответствующей стороны.
Другое важное свойство медианы заключается в том, что она сама является высотой треугольника. Высотой называется отрезок, соединяющий вершину треугольника с основанием перпендикулярно этому основанию. Таким образом, медиана также является высотой, проведенной из вершины к противоположной стороне.
Медиана треугольника имеет ряд интересных свойств. Например, сумма длин медиан треугольника равна трехкратной длине высоты. Также можно отметить, что медианы делят треугольник на шесть треугольников равной площади. Это свойство можно использовать для доказательства теоремы о площади треугольника с помощью медиан.
Исследуя свойства медиан треугольника, мы можем заметить, что длина медианы всегда меньше полупериметра треугольника. Это следует из того, что медиана делит сторону пополам, и, следовательно, ее длина всегда меньше половины суммы длин всех сторон.
Треугольник: понятие и свойства
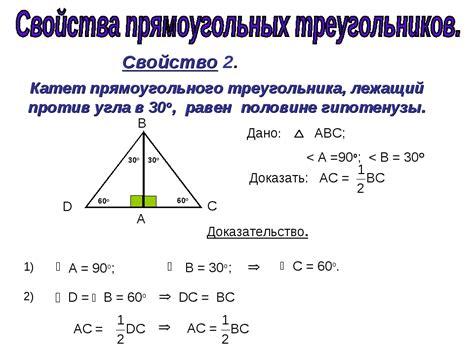
У треугольника есть несколько свойств:
- Углы треугольника: Сумма всех углов треугольника равна 180 градусов. Каждый угол в треугольнике может быть остроугольным (меньше 90 градусов), тупоугольным (больше 90 градусов) или прямым (равен 90 градусам).
- Стороны треугольника: Сторона треугольника - это отрезок, соединяющий две вершины треугольника. Сумма длин любых двух сторон треугольника всегда больше, чем длина третьей стороны.
- Высоты треугольника: Высота треугольника - это перпендикуляр, опущенный из одной вершины треугольника на противоположную сторону треугольника или ее продолжение. Высота делит сторону треугольника на две смежных части, пропорциональные отношению длины других сторон треугольника.
Треугольник - это одна из самых основных и понятных геометрических фигур. Изучение его свойств позволяет понять и применять множество теорем и закономерностей в геометрии.
Медиана треугольника: определение и конструкция

Медианы треугольника являются важными элементами его геометрической структуры. Они делят треугольник на три равные части и являются основой для дальнейших изучений свойств и характеристик треугольника.
Для построения медиан треугольника необходимо провести линии, соединяющие вершины треугольника с серединами противоположных сторон. Точки пересечения этих линий будут являться точками пересечения медиан и точкой пересечения всех трех медиан одновременно.
Медианы треугольника имеют ряд свойств и интересных геометрических особенностей. Одной из них является то, что медиана всегда проходит через центр тяжести треугольника. То есть, если провести через центр тяжести линию, параллельную одному из медиан, она будет пересекать точку пересечения всех медиан.
Также стоит отметить, что медиана треугольника всегда меньше его полупериметра. Это легко доказывается с помощью неравенства треугольника, поскольку медиана делит сторону треугольника на два равных отрезка. Следовательно, сумма длин медиан будет меньше суммы длин сторон треугольника, то есть медиана будет меньше его полупериметра.
Свойства медианы треугольника
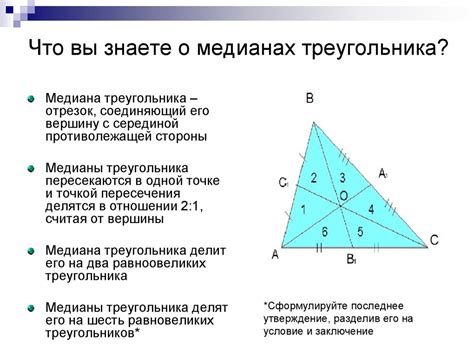
- Медиана треугольника – это отрезок, соединяющий вершину треугольника со средней точкой противолежащей стороны.
- Медиана делит себя и соответствующую сторону в отношении 2:1. То есть, длина медианы равна двум третям длины соответствующей стороны.
- Три медианы треугольника пересекаются в точке, называемой центром тяжести треугольника.
- Медиана является линией симметрии для треугольника. В этом отношении, длины сегментов медианы, ограниченные центром тяжести, равны.
- Медианы треугольника делят его на шесть треугольников равных площадей.
- Медиана длиннее высоты и меньше полупериметра треугольника.
Доказательство того, что медиана меньше полупериметра

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном доказательстве мы покажем, что длина медианы всегда меньше полупериметра треугольника.
Пусть a, b и c - стороны треугольника, а s - его полупериметр, определяемый формулой: s = (a + b + c) / 2.
Рассмотрим треугольник ABC, где медиана AM соединяет вершину A с серединой стороны BC.
Так как точка M делит сторону BC пополам, то BM = MC. По теореме Пифагора в треугольнике ABM: AM^2 = AB^2 - BM^2.
Аналогично, в треугольнике ACM: AM^2 = AC^2 - CM^2.
Просуммируем эти два уравнения: 2 · AM^2 = AB^2 + AC^2 - BM^2 - CM^2.
Так как BM = MC, то BM^2 + CM^2 = 2 · BM^2.
Подставляя это в предыдущее уравнение, получим: 2 · AM^2 = AB^2 + AC^2 - 2 · BM^2.
Мы знаем, что BM^2 = BC^2 / 4, так как точка M делит сторону BC пополам.
Подставляя это в предыдущее уравнение, получим: 2 · AM^2 = AB^2 + AC^2 - BC^2 / 2.
Так как AM медиана, то AM = BC / 2. Подставляя это в предыдущее уравнение, получим: BC^2 = AB^2 + AC^2 - 2 · AM^2.
Но заметим, что BC^2 = 4 · AM^2, так как AM = BC / 2. Подставляя это в предыдущее уравнение, получим: 4 · AM^2 = AB^2 + AC^2 - 2 · AM^2.
Приведем подобные слагаемые: 6 · AM^2 = AB^2 + AC^2.
Так как AM^2 = (BC / 2)^2 = BC^2 / 4, то 6 · BC^2 / 4 = AB^2 + AC^2.
Упрощаем: 3 · BC^2 / 2 = AB^2 + AC^2.
Так как AB, AC и BC - стороны треугольника, то AB > 0, AC > 0 и BC > 0. Тогда AB^2 > 0, AC^2 > 0 и BC^2 > 0.
Следовательно, мы можем заметить, что 3 · BC^2 / 2 > AB^2 и 3 · BC^2 / 2 > AC^2.
Таким образом, длина медианы AM = BC / 2 всегда меньше полупериметра треугольника (s = (AB + AC + BC) / 2).
Таким образом, мы доказали, что медиана треугольника всегда меньше его полупериметра.
Примеры и иллюстрации
Для лучшего понимания и визуализации доказательства того, что медиана треугольника меньше его полупериметра, рассмотрим следующие примеры и иллюстрации.
Пример 1:
На рисунке изображен треугольник ABC, со сторонами a, b и c. Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Пусть точка M - середина стороны BC. Медиана AM разделяет треугольник на две равные площади - S1 и S2. Очевидно, что S1 и S2 равны. Таким образом, площадь треугольника ABC равна 2 * S1. Полупериметр треугольника равен (a + b + c) / 2. Пусть это значение обозначим как P. Для доказательства того, что медиана треугольника меньше его полупериметра, заметим, что S1 = (1/2) * a * h, где h - высота треугольника, проведенная из вершины A. S1 можно выразить и через стороны треугольника: S1 = (1/2) * a * b * sin(C). Тогда площадь треугольника ABC равна: 2 * S1 = a * b * sin(C) = ac * sin(B) = bc * sin(A). Но bc * sin(A) |
Пример 2:
На данном рисунке представлен треугольник ABC с медианой AM. Заметим, что AM - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны BC. Развернем треугольник ABC, так чтобы сторона BC стала горизонтальной. Тогда медиана AM станет высотой треугольника. Пусть точка H - основание высоты. Так как AM является медианой, то она делит сторону BC пополам. Следовательно, BH = HC. Также можно заметить, что угол BMH = углу CMH, так как AM является медианой и делит сторону BC пополам, а угол BMH = углу CMH, так как у них общий угол MH. Таким образом, треугольники BMH и CMH равны по двум сторонам и углу между ними, поэтому они равны. Значит, BH = HC = MC. Теперь рассмотрим треугольник ABM. У него две равные стороны (AB и BM) и равный угол между ними (угол ABM). Значит, треугольник ABM равнобедренный. В равнобедренном треугольнике высота, проведенная из вершины и перпендикулярная к основанию, делит основание пополам. То есть, AH = HM. Таким образом, AH = HM = BH = HC = MC. Значит, медиана AM равна половине стороны BC. Поскольку полупериметр треугольника равен (a + b + c) / 2, и полупериметр треугольника всегда больше половины его стороны (BC |
Таким образом, на основе представленных примеров и иллюстраций можно убедиться в верности утверждения о том, что медиана треугольника меньше его полупериметра.





