Математический и общий естественнонаучный цикл представляет собой ключевые методологические принципы, которые позволяют различным наукам получать новые знания и расширять свой предметный объект. Этот цикл является обусловленным философскими исследованиями и активно применяется в науке с древних времен. Основная идея этого цикла заключается в возможности применения математической логики для верификации научных теорий и моделей.
Общий естественнонаучный цикл применяется во всех естественных науках и включает в себя следующие этапы: наблюдение, формулирование гипотезы, планирование и выполнение эксперимента, сбор данных, анализ результатов и формулирование заключений. В отличие от математического цикла, общий естественнонаучный цикл включает эксперименты или наблюдения, которые основаны на использовании специального оборудования и методик. Этот цикл играет важную роль в развитии физики, химии, биологии и других естественных наук и помогает расширить наши знания о природе и ее законах.
Математика: открытие закономерностей в числах и формулах

Один из первых и важных примеров открытия закономерностей в числах – развитие арифметики. Арифметика изучает основные математические операции, такие как сложение, вычитание, умножение и деление. Арифметические закономерности позволяют нам предсказывать результаты операций и решать сложные задачи.
Другой пример открытия закономерностей в числах – алгебра. Алгебра изучает общие законы и принципы решения уравнений и систем уравнений. При изучении алгебры мы обнаруживаем, что существуют определенные закономерности в поведении чисел и формул, которые позволяют нам решать различные задачи и находить общие решения.
Еще один пример открытия закономерностей в числах – геометрия. Геометрия изучает формы, размеры и отношения между объектами в пространстве. Закономерности в геометрии позволяют нам определить свойства фигур, вывести теоремы и доказывать их с использованием математической логики.
Открытие закономерностей в числах и формулах имеет огромное значение для различных областей науки и техники. Математические закономерности используются при решении задач в физике, экономике, компьютерных науках и многих других областях. Они позволяют нам понять мир вокруг нас и разрабатывать новые методы и технологии.
Математические доказательства и аксиоматика
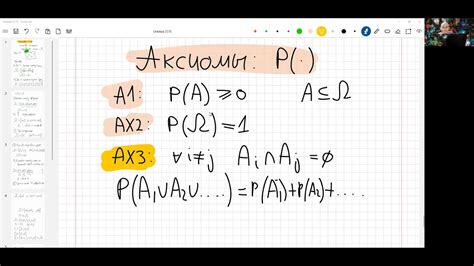
Аксиоматика - это система аксиом, то есть высказываний, которые не требуют доказательства и принимаются безусловно. Аксиомы являются основой для построения математических доказательств и теорий.
В математическом доказательстве обычно используются следующие логические операции:
- Дизъюнкция: возможны два варианта - или истинно утверждение А, или истинно утверждение В.
- Конъюнкция: истинно одновременно утверждение А и утверждение В.
- Отрицание: противоположное утверждение, в котором меняется истинность.
Математические доказательства базируются на строгой логике и следуют строгому порядку.
Математические доказательства играют важную роль во многих областях, включая алгебру, геометрию, анализ и теорию вероятностей. Они помогают устанавливать и выявлять закономерности и связи между математическими объектами, а также обеспечивают надежность и точность математических результатов.
Примеры математических законов и теорем

Теорема Пифагора: Основанный на отношении между сторонами прямоугольного треугольника, этот закон утверждает, что квадрат гипотенузы равен сумме квадратов катетов. Теорема Пифагора является одной из самых фундаментальных и полезных в геометрии.
Уравнение Эйлера: Это уравнение связывает пять из самых важных математических констант: число e, основание натурального логарифма, мнимая единица i, пи, и единицу. Уравнение Эйлера имеет красивую и элегантную формулу e^iπ + 1 = 0, которая выражает связь между этими константами.
Теорема Ферма: Это огромная сложная проблема, которая задумывает, что невозможно найти целочисленное решение уравнения x^n + y^n = z^n для n больше 2. Теорема Ферма была сформулирована Пьером де Ферма в 1637 году, но ее доказательство было найдено только в 1994 году Андрю Уайлсом.
Закон больших чисел: Этот закон утверждает, что при достаточно большом количестве независимых случайных величин их среднее арифметическое приближается к математическому ожиданию с ростом количества экспериментов. Закон больших чисел является основой статистики и вероятностных расчетов.
Это лишь некоторые примеры из множества математических законов и теорем, которые применяются в научных и практических областях. Математика является языком, позволяющим нам понять и описать мир вокруг нас, и эти законы и теоремы являются фундаментальными для этого.
Естественные науки: открытие законов и явлений природы

Основной метод, используемый в естественных науках, - это эксперимент. Ученые проводят серию наблюдений и измерений, чтобы проверить гипотезу о существовании определенного закона или отношения. При этом важно учитывать разные факторы, которые могут влиять на результаты эксперимента.
Открытие законов и явлений природы требует от ученых критического мышления и тщательного анализа данных. Они должны быть готовы изменить свои представления, если новые факты или эксперименты противоречат имеющимся теориям или концепциям.
Другим примером является закон всемирного тяготения, открытый Исааком Ньютоном. Он провел эксперименты и сформулировал закон, который объясняет притяжение между телами и движение планет вокруг Солнца.
Естественные науки играют важную роль в нашей жизни, помогая нам понять окружающий мир и создавать новые технологии. Они дают нам возможность преобразовывать природные явления в прогнозируемые процессы и использовать их в нашу пользу.
В целом, открытие законов и явлений природы - это важный этап в развитии естественных наук. Он позволяет нам расширить наши знания и постоянно усовершенствовать наши представления о мире.
Научный метод и эксперимент

Одним из главных инструментов научного метода является эксперимент, который заключается в тщательном изучении явления путем наблюдения и контролируемого изменения определенных параметров. Эксперимент должен быть правильно спланирован и выполняться с должной тщательностью, чтобы получить достоверные результаты.
Важным аспектом эксперимента является формулирование гипотезы, то есть предположения о связи между исследуемыми переменными. Гипотезы должны быть конкретными, проверяемыми и иметь четкие критерии для определения их истинности или ложности.
Научный метод и эксперимент – это важные инструменты, которые позволяют исследователям получать новые знания и развивать науку. С их помощью ученые могут расширять наши знания о природе и применять их в практических областях для улучшения нашей жизни.
Примеры открытий в физике, химии и биологии

Открытия в науке играют важную роль в понимании мира вокруг нас. Прогресс в физике, химии и биологии позволяет нам получать новые знания и развивать технологии, которые существенно влияют на нашу жизнь.
Физика
В физике было множество важных открытий, которые изменили наше понимание о физических явлениях. Одним из самых значительных открытий является закон всемирного тяготения, сформулированный Исааком Ньютоном. Этот закон позволяет объяснить движение небесных тел и стал одним из фундаментальных принципов физики.
Химия
В химии также было много важных открытий, которые стали основой для развития промышленности и медицины. Одним из таких открытий было открытие периодической системы элементов Дмитрием Менделеевым. Это классификация химических элементов, которая позволяет организовать их по возрастанию атомного номера и установить связи между ними.
Биология
В биологии мы наблюдаем постоянные открытия новых видов и принципов жизни. Одним из самых значимых открытий была структура ДНК, сделанная Джеймсом Ватсоном и Фрэнсисом Криком. Это открытие позволило понять принципы наследственности и развитие молекулярной биологии.



