Информатика - это наука, занимающаяся изучением структур, свойств и преобразований информации. Один из основных инструментов информатики - математическая модель. Математическая модель - это абстрактное представление реального явления или процесса с помощью математических символов и формул.
Математическая модель позволяет упростить сложные системы и процессы до такой степени, что их можно анализировать и предсказывать с помощью математических методов. Она позволяет исследовать различные аспекты информационных систем, такие как структура, функции и поведение.
Включение математической модели в информатику обеспечивает точность и надежность анализа информационных систем. Она позволяет определить связи между различными элементами системы и предсказывать их взаимодействие. Кроме того, математическая модель позволяет разрабатывать новые информационные системы, оптимизировать их работу и изучать возможные варианты усовершенствования.
Таким образом, математическая модель является важным инструментом информатики, который позволяет более глубоко исследовать и анализировать информационные системы, а также разрабатывать новые и улучшать уже существующие.
Что такое математическая модель?

Математическая модель состоит из двух основных компонентов:
- Представление реальной системы: Математическая модель должна адекватно отражать сущность и структуру реальной системы или явления. Это может быть любая система - от физических объектов до биологических процессов, от экономических рынков до социальных сетей.
- Математические символы и уравнения: Чтобы описать и анализировать систему, математическая модель использует формулы, уравнения и символы. Эти математические элементы представляют свойства и взаимодействия компонентов системы.
Математическая модель позволяет проводить различные исследования и эксперименты с системой в виртуальной среде. Она может помочь предсказать поведение системы в разных условиях, оптимизировать её параметры или принять эффективные решения на основе анализа модели. Она также может быть использована для создания компьютерных программ и моделирования реальных систем.
В информатике математические модели широко используются для анализа и оптимизации алгоритмов, для проектирования и анализа баз данных, для исследования сложных систем и для многих других задач. Они позволяют более точно и эффективно решать задачи информатики и создавать новые технологии.
Роль математической модели в информатике
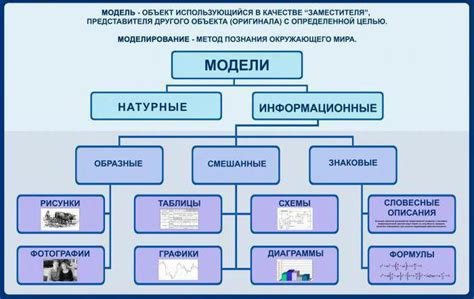
Математическая модель представляет собой упрощенное абстрактное описание реального объекта или процесса, состоящее из математических символов, уравнений и графических представлений. Она позволяет формализовать исследуемую систему, выявить ее основные свойства, прогнозировать результаты и проводить эксперименты без прямого вмешательства в реальный объект или процесс.
В информатике математическая модель используется для моделирования и анализа различных аспектов информационных систем, например:
| Тип информационной системы | Примеры математических моделей |
|---|---|
| Сети передачи данных | Модель теории графов |
| Алгоритмы и вычисления | Математическая модель сложности алгоритмов |
| Базы данных | Модель реляционной алгебры |
| Искусственный интеллект | Математическая модель нейронных сетей |
Математическая модель позволяет анализировать и оптимизировать процессы в информационных системах, предсказывать их поведение и принимать обоснованные решения на основе математических методов и экспериментов. Она позволяет повысить эффективность работы информационных систем, улучшить качество программного обеспечения и разработать новые алгоритмы и подходы к решению задач в информатике.
Использование математической модели в алгоритмах
Математическая модель может быть использована для описания различных аспектов алгоритмов, включая время выполнения, использование памяти, эффективность и точность. Она может помочь в оптимизации алгоритмов, позволяя предсказать их производительность при различных входных данных, а также находить наилучшие параметры для достижения оптимальных результатов.
Использование математической модели также позволяет проводить анализ сложности алгоритмов и сравнивать их эффективность. Оно позволяет оценивать, насколько быстро работает алгоритм в сравнении с другими алгоритмами или с идеальным алгоритмом. Также математическая модель может помочь в предсказании времени исполнения алгоритма в различных ситуациях и установить границы его применимости.
Математическая модель может быть представлена в виде графов, матриц, уравнений или других абстрактных структур, что позволяет упростить анализ и понять основные принципы работы алгоритмов. Использование математической модели в алгоритмах улучшает понимание их поведения, что помогает разработчикам создавать более эффективные и оптимальные решения.
Применение математической модели в анализе данных

В современном мире объемы данных, собираемых и хранящихся компаниями, учреждениями и государствами, растут в геометрической прогрессии. Однако, сырые данные сами по себе не представляют ценность. Для их превращения в полезную информацию и сделать на основе нее осознанные решения, требуется проведение анализа данных.
Математическая модель разработана для помощи в анализе и обработке данных. Она представляет собой формализованное описание явлений и процессов с использованием математических средств. Математическая модель может быть использована для идентификации закономерностей, прогнозирования и оптимизации процессов.
Одним из основных применений математической модели в анализе данных является прогнозирование. Путем математического моделирования можно предсказать различные события и тенденции на основе имеющихся данных. Например, на основе исторических данных о продажах можно предсказать будущий спрос на товары или услуги, что позволит оптимизировать производство и планирование.
Еще одно важное применение математической модели в анализе данных - оптимизация. Математическая модель может использоваться для нахождения оптимальных решений в различных сферах, например, в логистике или финансовом планировании. С помощью математической модели можно определить оптимальные маршруты доставки товаров или оптимальное распределение финансовых ресурсов.
Таким образом, математическая модель в анализе данных играет ключевую роль в преобразовании больших объемов данных в информацию, которая может быть использована для принятия осознанных решений. Применение математической модели позволяет предсказывать и оптимизировать различные процессы, что способствует достижению высокой эффективности и прогресса в различных сферах деятельности.
Основные составляющие математической модели в информатике
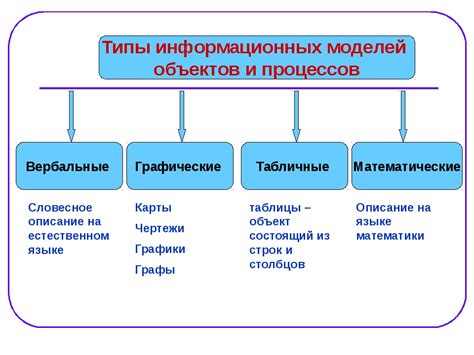
Одной из основных составляющих математической модели в информатике является формализм. Формализм представляет собой систему символов и правил, позволяющих описать определенные объекты и взаимодействия между ними. Формализмы используются для описания языков программирования, алгоритмов, сетевых протоколов и других аспектов информатики.
Еще одной важной составляющей математической модели является математическая структура. Математическая структура определяет набор элементов и операций над ними. В информатике математические структуры используются для описания данных и их обработки. Некоторые примеры математических структур в информатике включают множества, графы, матрицы, деревья и другие.
Также важным элементом математической модели является функция. Функция - это отображение между двумя множествами, где каждому элементу первого множества соответствует единственный элемент второго множества. В информатике функции используются для описания операций и взаимодействий в компьютерных системах. Например, функции могут описывать вычисления, передачу данных или другие процессы.
Таким образом, основные составляющие математической модели в информатике включают формализм, математические структуры, функции, моделирование и анализ. Эти компоненты помогают описать и анализировать различные аспекты компьютерных систем и процессов, что является важной задачей в информатике.
Формализация задачи в математической модели
Для формализации задачи могут использоваться различные подходы. Некоторые задачи могут быть формализованы с помощью алгоритмов или математических уравнений. Другие задачи могут требовать использования структур данных или логического программирования.
При формализации задачи необходимо учесть все аспекты и особенности, которые могут влиять на ее решение. Например, при решении задачи оптимизации необходимо учесть ограничения и целевую функцию. При формализации задачи на графах необходимо учесть вершины, ребра и связи между ними.
Формализация задачи позволяет сделать ее конкретной и однозначной, что упрощает разработку математической модели и позволяет проводить точные вычисления. Однако, важно помнить о том, что формализация задачи может включать в себя только те аспекты, которые могут быть выражены с помощью математических символов и операций.
Выбор и применение математических методов

Одним из основных критериев выбора математического метода является его пригодность для решения конкретной задачи. Разные математические методы могут иметь разные предположения и ограничения, поэтому важно оценить, насколько метод соответствует требованиям поставленной задачи.
Ещё одним важным критерием выбора математического метода является его эффективность. Некоторые математические методы могут иметь низкую скорость работы или требовать большого количества ресурсов, что может быть неприемлемо для конкретной задачи. Поэтому необходимо учитывать и оценивать время и ресурсы, которые требуются для применения выбранного метода.
Также важно учитывать степень формализации, которую предоставляет выбранный математический метод. Некоторые методы могут предоставлять точные и строгое формализованное решение, в то время как другие могут быть более приближенными и не столь формализованными. Выбор метода должен быть основан на потребностях и требованиях конкретной задачи.
Таким образом, при выборе и применении математических методов в информатике необходимо учитывать пригодность метода для конкретной задачи, его эффективность и степень формализации. Это позволит построить математическую модель, которая будет наиболее точно соответствовать реальности и решать поставленные задачи.
Верификация и валидация математической модели

Верификация – это процесс проверки математической модели на соответствие ее спецификации. Он включает в себя формальный анализ модели и ее элементов, а также проверку правильности математических выкладок и решения уравнений. В результате верификации можно убедиться, что математическая модель действительно представляет реальные процессы и явления.
Валидация – это процесс проверки математической модели на соответствие реальности. Он включает в себя сравнение результатов моделирования с экспериментальными данными или наблюдениями. В ходе валидации можно убедиться, что математическая модель адекватно описывает изучаемую систему и предсказывает ее поведение в различных условиях.
Для проведения верификации и валидации математической модели часто используются различные методы и техники. Например, можно провести статический анализ модели на основе математических доказательств или выполнить серию экспериментов для сравнения результатов моделирования с реальными данными.
Верификация и валидация математической модели являются важными компонентами процесса создания информационной системы. Они позволяют убедиться в надежности и правильности модели, а также обеспечить ее пригодность к использованию в реальных условиях. Эти этапы помогают разработчикам и исследователям улучшить и оптимизировать модель, а также сделать более точные прогнозы и предсказания.



