Линия пересечения плоскостей является одним из важных понятий геометрии, изучаемых в 10 классе. Это особый объект, который возникает тогда, когда две плоскости имеют общую точку пересечения. Линия пересечения может быть прямой, кривой или отрезком, в зависимости от свойств плоскостей.
Если плоскости пересекаются под прямым углом, то линия пересечения будет прямой линией. Если плоскости наклонны друг к другу, то линия пересечения будет кривой. Кроме того, линия пересечения может быть бесконечной в том случае, когда плоскости параллельны друг другу.
Линия пересечения плоскостей играет важную роль в различных геометрических задачах. Она может быть использована для определения положения точки относительно двух плоскостей, для построения пересечения двух плоскостей или для определения угла между плоскостями.
Методы определения линии пересечения плоскостей могут быть различными. Одним из них является использование системы уравнений плоскостей. Другой метод - использование понятия нормального вектора к плоскости. Изучение линии пересечения плоскостей позволяет шире понять геометрические принципы и развить навыки пространственного мышления.
Линия пересечения плоскостей в 10 классе
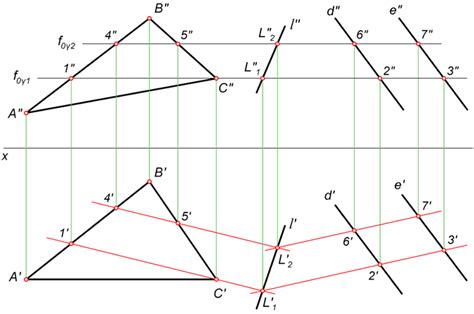
Линией пересечения плоскостей называется прямая, образованная точками, в которых пересекаются две плоскости. Это важное понятие, которое изучается в 10 классе в рамках курса геометрии.
Для определения линии пересечения необходимо иметь две плоскости. В учебниках часто используются примеры с плоскостями, заданными уравнениями. Например, уравнение первой плоскости может быть записано в виде: A1x + B1y + C1z + D1 = 0, а уравнение второй плоскости: A2x + B2y + C2z + D2 = 0. Здесь A, B, C и D - коэффициенты, а x, y и z - переменные.
Для определения линии пересечения необходимо решить систему уравнений плоскостей. После нахождения значения переменных x, y и z можно составить уравнение прямой, проходящей через эти точки.
Линия пересечения плоскостей может иметь различные характеристики. Например, она может быть прямой или кривой, ограниченной или неограниченной. Эти характеристики зависят от свойств плоскостей и их взаимного положения.
Изучая линию пересечения плоскостей в 10 классе, ученики получают представление о трехмерной геометрии и научатся анализировать пространственные объекты. Это важные навыки, которые будут полезны в дальнейшем изучении математики и связанных с ней дисциплинах.
Определение линии пересечения плоскостей
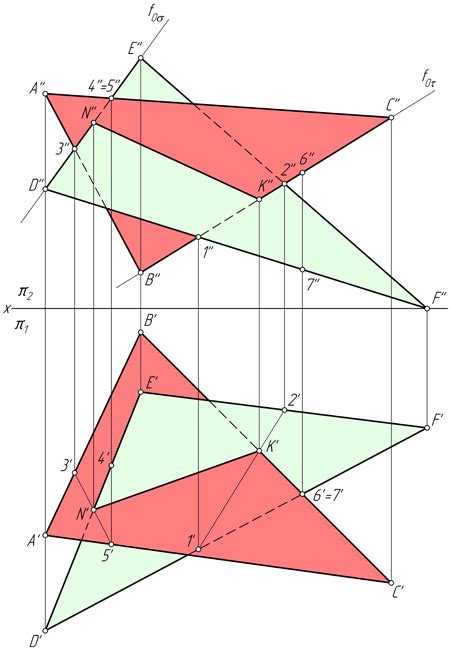
Когда две плоскости пересекаются, они могут иметь либо одну общую точку, либо общую прямую - линию пересечения. Линия пересечения может быть прямой или кривой, в зависимости от расположения плоскостей, но в школьном курсе геометрии обычно рассматривается только прямая линия пересечения.
Для определения линии пересечения плоскостей можно использовать систему уравнений двух плоскостей и решить эту систему. В результате получится уравнение прямой, которая будет описывать линию пересечения этих плоскостей.
Линия пересечения плоскостей является важным понятием в трехмерной геометрии и находит применение в различных областях, например, в инженерии, архитектуре и физике. Ее изучение позволяет углубить понимание пространственных отношений и решать задачи, связанные с пересечением плоскостей.
Геометрическое представление линии пересечения плоскостей
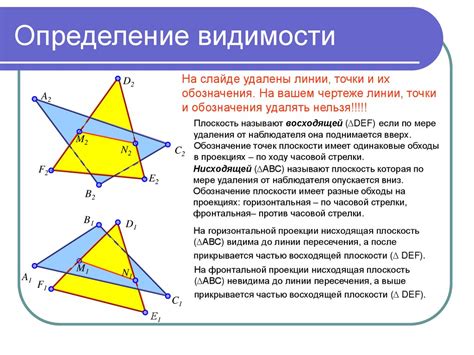
Для того чтобы визуализировать линию пересечения плоскостей, можно представить себе ситуацию, когда две плоскости пересекаются и образуют некоторую линию. Эта линия может быть прямой или изогнутой. Она может быть горизонтальной, вертикальной или наклонной.
Однако, линия пересечения плоскостей не всегда существует. Если две плоскости параллельны, то они не имеют общих точек и, следовательно, не имеют линии пересечения. Если две плоскости совпадают, то они имеют бесконечно много общих точек и, таким образом, линия пересечения также бесконечна.
Для определения геометрического представления линии пересечения плоскостей можно использовать различные методы, такие как пространственная репрезентация с помощью моделей или чертежей, математическое определение с использованием уравнений плоскостей и пересечение их параметрических уравнений.
Геометрическое представление линии пересечения плоскостей важно для решения многих геометрических задач, например, при определении точки пересечения прямой и плоскости или при построении сечений тел.
Уравнение линии пересечения плоскостей
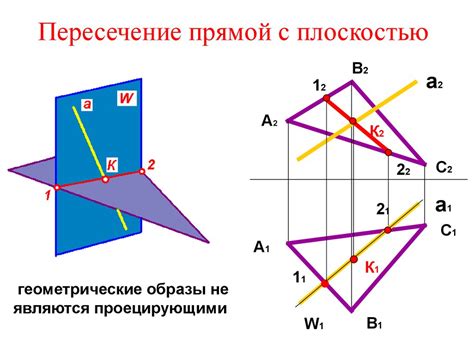
Рассмотрим две плоскости в пространстве, заданные уравнениями:
Аx + Вy + Сz + D₁ = 0
Аx + Вy + Сz + D₂ = 0
Для нахождения уравнения линии пересечения этих плоскостей необходимо решить систему уравнений, состоящую из уравнений этих плоскостей. После решения системы получим значения переменных x, y и z.
Уравнение линии пересечения будет иметь вид:
x = x₀ + at
y = y₀ + bt
z = z₀ + ct
где (x₀, y₀, z₀) - координаты точки, через которую проходит линия пересечения, a, b и c - коэффициенты, определяющие направление линии, t - параметр, изменяющийся в некотором интервале.
Таким образом, уравнение линии пересечения плоскостей позволяет описать эту линию в трехмерном пространстве с помощью параметрических уравнений.
Нахождение точек пересечения линии с осями координат
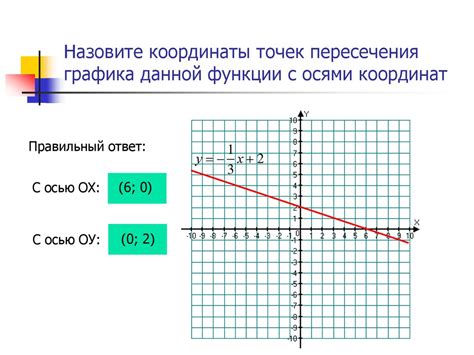
Линия пересечения плоскостей может быть представлена в виде уравнения. Чтобы найти точки пересечения линии с осями координат, необходимо подставить соответствующие значения координат в уравнение линии. В результате получаются точки, в которых линия пересекает оси координат.
Если уравнение линии имеет вид x = a, то точка пересечения с осью ординат будет иметь координаты (a, 0). Это происходит потому, что при x = a, y всегда будет равно 0.
В случае, когда уравнение линии имеет вид y = b, то точка пересечения с осью абсцисс будет иметь координаты (0, b). Здесь x всегда будет равно 0, а y будет равно b.
Таким образом, зная уравнение линии, мы можем найти точки пересечения линии с осями координат и определить их координаты.
Примеры задач на линию пересечения плоскостей
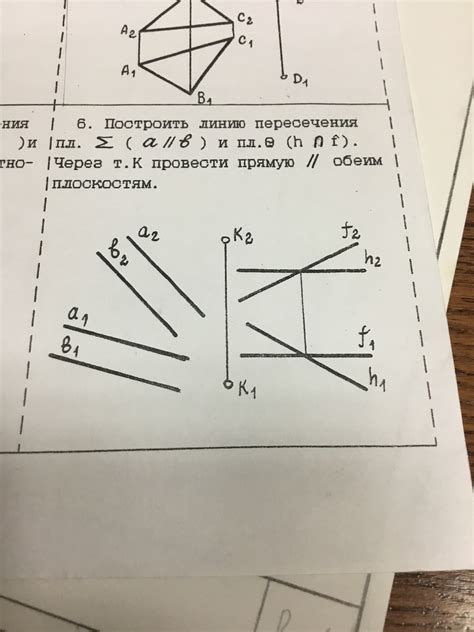
Рассмотрим несколько примеров задач, в которых требуется найти линию пересечения плоскостей:
- Задача 1: Даны две плоскости, заданные уравнениями: 2x - y + 3z = 4 и x + 3y - z = 2. Найти уравнение прямой, образующей их пересечение.
- Задача 2: Найти точку пересечения плоскостей, заданных уравнениями: 2x + 3y - z = 1 и x - 2y + 2z = -4.
- Задача 3: Даны три плоскости, заданные уравнениями: x + y + z = 3, 2x - 3y + z = 4 и x - 2y - z = 1. Найти расстояние между плоскостями.
Чтобы решить данную задачу, нужно составить систему уравнений, в которой будут участвовать коэффициенты при переменных x, y и z. Затем решить эту систему методом Гаусса. Получив уравнение прямой, можно определить ее параметрическое представление или уравнение в отрезках.
Для решения данной задачи, можно воспользоваться методом Крамера. Составим систему уравнений, где каждая плоскость представлена уравнением, а каждая переменная - координатой точки пересечения. Решив эту систему, найдем координаты искомой точки.
Для решения данной задачи, можно воспользоваться формулой для расстояния между плоскостями. Составим систему уравнений, в которой будут участвовать коэффициенты при переменных x, y и z. Подставим найденные коэффициенты в формулу и найдем расстояние между плоскостями.
Таким образом, решая задачи на линию пересечения плоскостей, мы можем определить уравнение прямой, точку пересечения или расстояние между плоскостями.
Применение линии пересечения плоскостей в реальной жизни
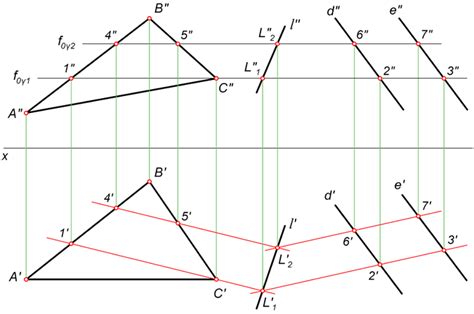
Одной из областей, где линия пересечения плоскостей находит применение, является архитектура и строительство. При проектировании зданий и сооружений, инженеры и архитекторы используют линию пересечения плоскостей для определения точек пересечения стен и других конструкций. Это позволяет им создавать прочные и устойчивые здания.
Еще одним примером применения линии пересечения плоскостей является машиностроение. В процессе разработки и создания различных механизмов и машин, инженеры используют линию пересечения плоскостей для определения точек контакта, движения и взаимодействия различных частей и деталей. Это позволяет им создавать эффективные и надежные механизмы.
А еще линия пересечения плоскостей используется в геодезии. Геодезисты, работающие на местности и проводящие измерения, используют линию пересечения плоскостей для определения точного местоположения объектов и для построения карт и планов.
Конечно, это только некоторые примеры применения линии пересечения плоскостей в реальной жизни. Они показывают, что геометрия имеет практическое значение и применима в различных областях нашей жизни.
Связь линии пересечения плоскостей с другими геометрическими объектами
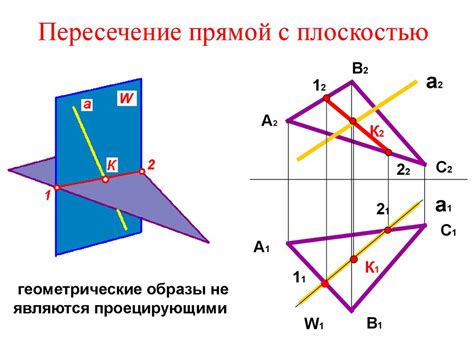
Линия пересечения плоскостей в геометрии играет важную роль и имеет связь с другими геометрическими объектами. Рассмотрим несколько примеров таких связей:
| Геометрический объект | Связь с линией пересечения плоскостей |
|---|---|
| Угол между плоскостями | Линия пересечения плоскостей является основой для измерения угла между ними. При нахождении угла мы используем точки, лежащие на линии пересечения плоскостей. |
| Прямая, лежащая в плоскости | Если прямая лежит в одной из плоскостей, пересекающихся на линии пересечения, то она будет пересекать эту линию и создавать точки пересечения. |
| Трехмерные фигуры | Линия пересечения плоскостей может быть осью симметрии для трехмерных фигур, если они симметричны относительно этой линии. Например, если плоскости пересекаются под прямым углом, то эта линия будет осью симметрии для куба. |
Таким образом, линия пересечения плоскостей не только позволяет определить угол между плоскостями, но и влияет на взаимное расположение других геометрических объектов в пространстве.



