В математике куб – это геометрическое тело, образованное с помощью правильного шестиугольника, который вытянули в пространство. Куб имеет шесть граней, все его грани являются квадратами и равны по размеру. Также куб имеет двенадцать ребер и восемь вершин. Куб обладает некоторыми уникальными свойствами, которые делают его особенным и интересным для изучения.
Все грани куба являются квадратами, у которых все стороны равны между собой. Такая особенность делает куб особенно удобным для решения задач в математике. Например, если нам известна площадь одной грани куба, мы можем легко найти площади остальных граней. Для этого нужно применить формулу для нахождения площади квадрата, в которой нужно возвести в квадрат длину стороны куба.
Куб также обладает другой интересной особенностью – его объем. Объем куба можно найти, возводя в куб длину одной из его сторон. Например, если у нас есть куб с длиной стороны 5 см, то его объем можно найти с помощью формулы V = a³, где V – объем куба, а – длина стороны куба. В нашем случае, V = 5³ = 5 * 5 * 5 = 125 см³.
Куб в математике 5 класс
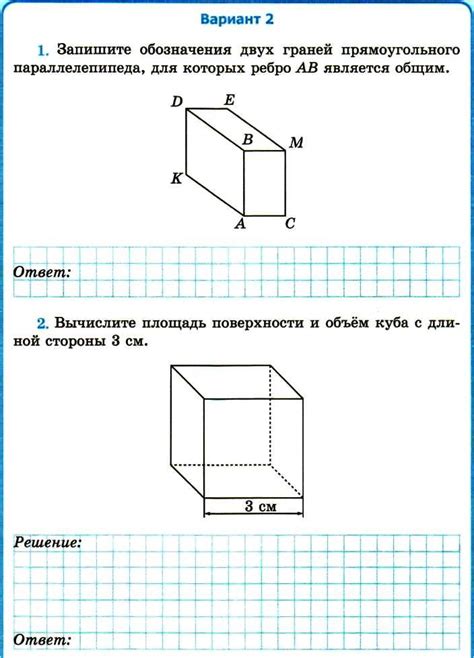
Для понимания куба необходимо знать следующие понятия:
- Грань куба - это каждая из шести прямоугольных поверхностей, из которых состоит куб.
- Вершина куба - это точка, где сходятся три ребра куба.
- Ребро куба - это отрезок, соединяющий две смежные вершины куба.
- Диагональ - это отрезок, соединяющий две несмежные вершины куба.
В 5 классе дети начинают изучать свойства куба, такие как:
- Все грани куба являются квадратами одинаковой площади.
- Все углы куба прямые (равны 90 градусам).
- Объем куба равен кубу длины его ребра: V = a^3, где a - длина ребра.
- Площадь поверхности куба равна удвоенной площади одной из его граней: S = 6a^2, где a - длина ребра.
Кубы можно встретить не только в математике, но и в реальной жизни. Например, в зернохранилищах, игральных костях, и многих других предметах. Понимание свойств куба помогает решать задачи и рассуждать логически.
Определение куба
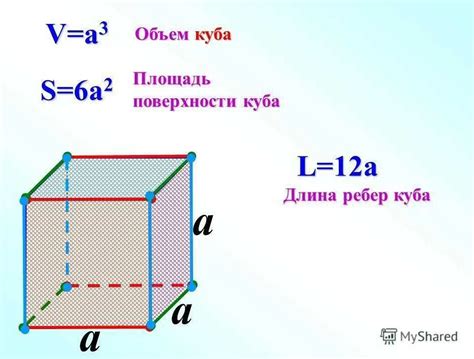
Куб считается особым случаем параллелепипеда, у которого все грани являются квадратами. Куб имеет три оси симметрии: горизонтальную ось, вертикальную ось и ось, проходящую через его центр и две противоположные вершины.
Обозначение: в математике куб обычно обозначается символом "a³", где "a" - длина стороны куба.
Свойства куба
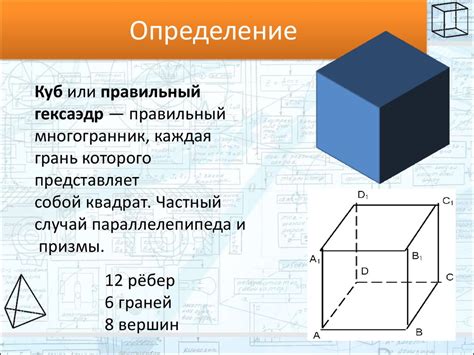
Свойства куба:
- Ребра и грани: У куба 6 граней, 12 ребер и 8 вершин. Все грани куба являются квадратами, а все его ребра имеют одинаковую длину.
- Углы: Все углы куба равны 90 градусам, что делает его прямоугольным и особенно удобным для многих математических и геометрических рассуждений.
- Диагонали: Диагональ любой грани куба является еще одним ребром. Диагонали граней, которые проходят через центр куба, делят его на 8 равных тетраэдров.
- Объем и площадь: Объем куба рассчитывается по формуле V = a^3, где a представляет собой длину его ребра. Площадь поверхности куба рассчитывается по формуле S = 6a^2, где a - длина ребра.
- Симметрия: Куб обладает множеством осей симметрии. Он имеет 3 оси симметрии, которые проходят через центры противоположных граней, а также 4 оси симметрии, которые проходят через противоположные вершины.
Куб - важная геометрическая фигура, которая находит широкое применение в различных математических и инженерных задачах. Понимание его свойств помогает развивать пространственное мышление и решать сложные задачи в различных областях.
Расчет объема куба
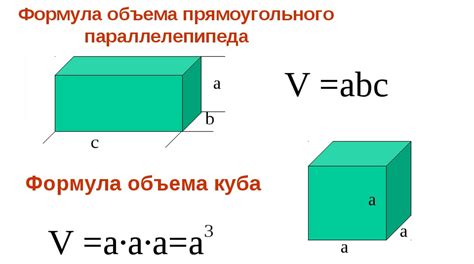
Чтобы вычислить объем куба, необходимо знать длину его ребра. Объем куба определяется формулой:
| Формула | V = a * a * a |
| где V | - объем куба, |
| a | - длина ребра. |
Для примера, если длина ребра куба равна 5 см, то объем куба можно вычислить следующим образом:
| a | = 5 см |
| V | = 5 см * 5 см * 5 см |
| V | = 125 см³ |
Таким образом, объем куба со стороной 5 см равен 125 кубическим сантиметрам (см³).
При решении задач на расчет объема куба необходимо помнить, что единицы измерения длины должны соответствовать единицам объема. В нашем примере, если длина ребра была указана в сантиметрах (см), то и объем куба будет выражен в кубических сантиметрах (см³).
Площадь боковой поверхности куба
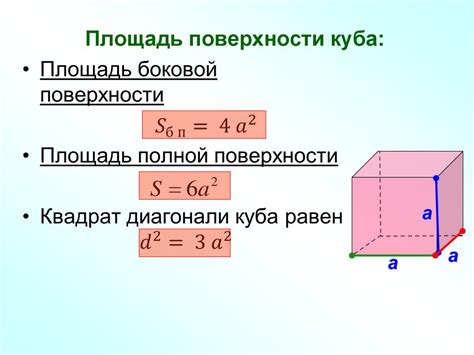
Площадь боковой поверхности куба можно вычислить по формуле:
S = 4 * a * a,
где a - длина стороны куба. Формула основана на том факте, что у куба все стороны равны друг другу.
Для вычисления площади боковой поверхности куба ученикам необходимо знать длину стороны куба. Они могут использовать формулы или измерять сторону куба с помощью линейки.
Зная площадь боковой поверхности куба, ученикам станет легче понимать и решать различные задачи, связанные с геометрией и пространственными представлениями.
Связь куба с другими геометрическими фигурами

Куб является простейшим видом параллелепипеда, а также является прямым правильным многогранником.
У куба много связей с другими геометрическими фигурами:
1. Квадрат
Куб является трехмерной версией двумерного квадрата. Все грани куба – квадраты, поэтому все свойства, применимые к квадрату, также применимы к каждой грани куба. Например, все стороны квадрата и соответствующих граней куба равны по длине.
2. Параллелепипед
Параллелепипед – это тело, у которого все грани являются параллелограммами. Куб является специальным видом параллелепипеда, в котором все грани – квадраты. Поэтому куб можно рассматривать как частный случай параллелепипеда.
3. Пирамида
Куб можно рассматривать как пирамиду с квадратной основой. Верхний угол куба будет вершиной пирамиды, а каждая его грань будет боковой гранью пирамиды.
4. Ромб
Если соединить центры противоположных граней куба, получится ромб. Ромб – это четырехугольник, у которого все стороны равны. Свойства ромба применяются в рассуждениях и задачах, связанных с кубами.
5. Октаэдр
Если провести диагонали между центрами противоположных граней куба, получится октаэдр – многогранник, состоящий из восьми граней. Каждая грань октаэдра будет треугольником.
Таким образом, куб является основой для изучения и понимания других геометрических фигур, расширяя наши знания о трехмерном пространстве и его свойствах.
Построение куба

Для построения куба необходимы следующие шаги:
- Нарисуйте горизонтальную прямую линию, которая будет служить основанием куба.
- Начертите вертикальные линии из обоих концов основания.
- Из каждой точки, где вертикальные линии пересекаются с основанием, нарисуйте горизонтальные линии.
- Соедините концы горизонтальных линий, которые находятся на одном уровне, чтобы получить боковые грани куба.
- Восстановите отсутствующие ребра куба, соединяя разные грани друг с другом.
- Добавьте ребра, отходящие от каждой вершины к основанию. Убедитесь, что все ребра имеют одинаковую длину.
- Окрасьте грани куба для лучшей визуализации.
Построение куба с помощью указанных шагов поможет лучше понять его структуру и свойства. Это важно для изучения различных математических концепций, таких как объем и площадь поверхности.
Важно: Чтобы получить точный и равносторонний куб, важно следовать инструкциям и проводить линии ровно и аккуратно.
Примеры задач с кубами

1. Вокруг куба с ребром 3 см нанесли однородную краску. Сколько получилось общей площади окрашенной поверхности?
| Сторона куба (см) | Площадь грани (см²) |
|---|---|
| 3 | 9 |
Площадь окрашенной поверхности куба равна площади всех его граней.
Так как каждая грань куба равна квадрату со стороной, равной ребру куба, то площадь грани равна 9 см².
Так как куб имеет 6 граней, то общая площадь окрашенной поверхности составляет 6 * 9 = 54 см².
2. Куб с ребром 5 см разрезали на маленькие кубики с ребром 1 см каждый. Сколько маленьких кубиков получилось?
Общее количество маленьких кубиков, полученных из большого куба, равно произведению количества кубиков по каждой стороне куба.
Так как сторона большого куба равна 5 см, то количество кубиков по каждой стороне равно 5.
Таким образом, общее количество маленьких кубиков составляет 5 * 5 * 5 = 125.
Использование кубов в реальной жизни

Кубы, а также другие геометрические тела, имеют не только теоретическое значение в математике, но и широкое практическое применение в реальной жизни.
Одним из примеров использования кубов является их применение в строительстве. Кубы могут быть использованы для создания фундамента здания, а также для построения ограждений и заборов. Благодаря своей геометрической форме, кубы обеспечивают стабильность и прочность конструкции.
Кубы также активно используются в упаковке. Они могут быть использованы для упаковки различных товаров, таких как книги, игрушки, электроника и многое другое. Благодаря своей регулярной форме, кубы позволяют удобно и компактно упаковывать товары, что упрощает их хранение и транспортировку.
Еще одним примером использования кубов в реальной жизни является их применение в играх и головоломках. Кубик Рубика - это известная головоломка, состоящая из множества маленьких кубиков, которые могут поворачиваться. Решение этой головоломки требует логического мышления и умения анализировать пространственные отношения между кубиками.
Кубы также используются в математических моделях. Они могут быть использованы для визуализации и изучения различных математических концепций, таких как объемы, площади и пропорции. Кубы могут помочь учащимся лучше понять и запомнить эти концепции, используя визуальную модель.



