Параллельные прямые – это важное понятие в геометрии, которое используется для описания линий, которые никогда не пересекаются. Кажется, что это очевидный факт, но давайте рассмотрим некоторые логические доказательства, которые подтверждают эту идею.
Доказательство 1: Предположим, что у нас есть две параллельные прямые A и B. Рассмотрим точку C на прямой A. Предположим, что они пересекаются в точке D. Заметим, что линия AB секает параллельные прямые A и B. Однако, по определению параллельных прямых, они не должны пересекаться.
Доказательство 2: Предположим, что у нас есть две параллельные прямые A и B. Рассмотрим две точки C и D на прямой A. Если бы они пересекали прямую B, тогда мы могли бы нарисовать треугольник ACB, в котором были бы два угла, сумма которых была бы равна 180 градусам. Однако, по свойству параллельных прямых, сумма углов треугольника должна быть равна 180 градусам. Следовательно, прямые A и B не могут пересекаться.
Таким образом, существует несколько методов доказательства того, что параллельные прямые никогда не пересекаются. Изучение этого факта является фундаментальным шагом в геометрии и играет важную роль в множестве математических концепций и приложений.
Параллельные прямые
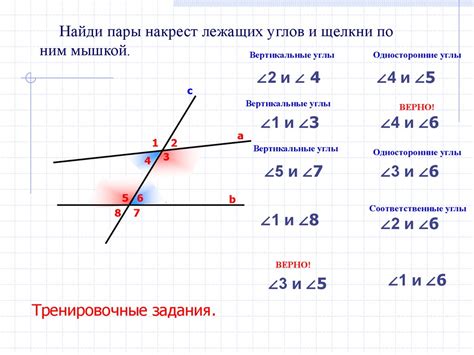
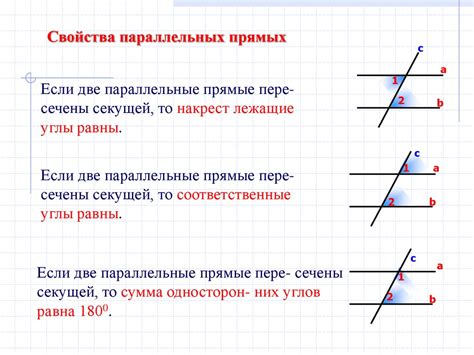
Для доказательства того, что параллельные прямые не пересекаются, можно использовать два важных свойства: свойство углов, образованных параллельными прямыми, и свойство противоположных углов.
Свойство углов: Если параллельные прямые пересекаются с третьей прямой, то сумма углов, образованных этой третьей прямой с параллельными, равна 180°. Это свойство помогает определить, что прямые параллельны, если их углы равны или дополнительны.
Свойство противоположных углов: Если две параллельные прямые пересекаются третьей прямой, то противоположные углы, образованные этой третьей прямой, равны. То есть, если углы имеют одну сторону на параллельных прямых, они равны.
С помощью этих свойств можно доказать, что параллельные прямые не пересекаются. Если параллельные прямые имели бы точку пересечения, то сумма углов, образованных другими прямыми с этими параллельными, была бы либо равна 180° (в случае равных углов), либо равна нулю (в случае дополнительных углов). Такие углы не могут быть одновременно равными и нулевыми, следовательно, параллельные прямые не пересекаются.
Что такое параллельные прямые?
Свойства параллельных прямых
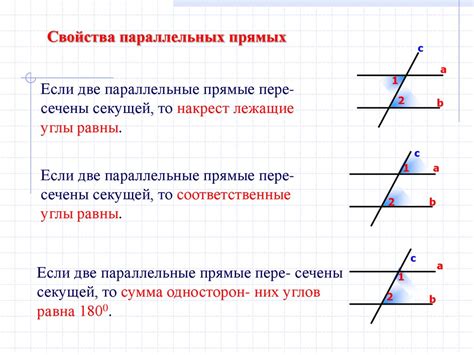
1. Не пересекаются.
Одно из основных свойств параллельных прямых заключается в том, что они не пересекаются. Это означает, что параллельные прямые движутся в одном направлении и никогда не встречаются в одной точке.
2. Имеют одинаковый угол наклона.
Другое свойство параллельных прямых заключается в том, что они имеют одинаковый угол наклона. Это означает, что если одна параллельная прямая наклонена под определенным углом к оси координат, то и остальные параллельные прямые будут иметь такой же угол наклона.
3. Расстояние между ними постоянно.
Третье свойство параллельных прямых заключается в том, что расстояние между ними постоянно. Это означает, что независимо от того, насколько большими или маленькими будут параллельные прямые, они всегда будут иметь одинаковое расстояние между собой.
Эти свойства параллельных прямых являются основополагающими для изучения геометрии и имеют большое практическое применение при решении задач нахождения точек пересечения прямых и плоскостей.
Пересечение параллельных прямых
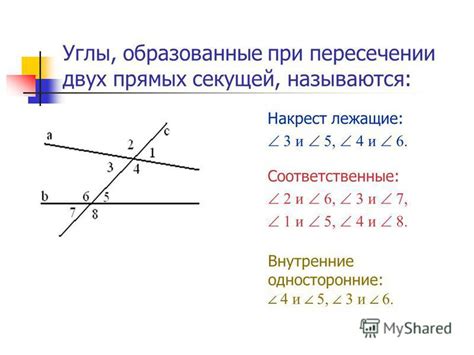
На плоскости параллельные прямые не пересекаются. Это свойство можно увидеть, анализируя их угловые коэффициенты.
Если две прямые имеют одинаковый угловой коэффициент, то они параллельны. Угловой коэффициент определяет наклон прямой и выражается отношением разности координат точек, через которые проходит прямая, к их разности по осям. Если данный коэффициент равен для двух прямых, то их наклоны одинаковы, и, следовательно, они параллельны.
Например, прямые с уравнениями у = 2х + 4 и у = 2х - 3 имеют одинаковый угловой коэффициент 2, и поэтому они параллельны. Это значит, что они не пересекаются ни в одной точке на плоскости.
Если у двух прямых разные угловые коэффициенты, то они непараллельны и обязательно пересекаются в некоторой точке. При этом можно вычислить координаты точки пересечения с помощью системы уравнений, составленных по данным прямым.
| Примеры | Уравнения параллельных прямых | Угловой коэффициент |
|---|---|---|
| Прямая 1 | у = 3х + 2 | 3 |
| Прямая 2 | у = 3х + 5 | 3 |
В таблице показаны две прямые с одинаковым угловым коэффициентом 3. Это означает, что они параллельны и не пересекаются на плоскости.
Гипотеза о пересечении параллельных прямых
Параллельные прямые – это прямые, которые не пересекаются ни в одной точке. Они находятся на одной плоскости и имеют одинаковый угол наклона. В связи с этим можно сформулировать такую гипотезу: две прямые, которые никогда не пересекаются, всегда будут параллельными.
Однако данная гипотеза пока не является аксиоматически доказанной теоремой. Доказательство этой гипотезы является одной из задач в математике.
Исторические исследования показывают, что гипотеза о пересечении параллельных прямых привлекала внимание многих математиков и ученых. Известно, что такие великие умы, как Евклид и Гаусс, также задавались этим вопросом.
Современные математики сталкиваются с вызовом при попытке доказать данную гипотезу. Безопасная альтернатива состоит в принятии гипотезы как аксиомы, что позволяет строить математические размышления и рассуждения.
Как и любая гипотеза, она может быть как принята, так и опровергнута. В будущем это может быть решено путем разработки новых теорий и доказательств.



